Astronet > Forumy > Obsuzhdenie publikacii Astroneta > Re: Vneshnyaya ballistika pnevmaticheskogo oruzhiya

po tekstam po forumu vnutri temy

args[0]=message
args[1]=DB::DB::Message=HASH(0x2d4a5a0)
Re: Vneshnyaya ballistika pnevmaticheskogo oruzhiya
1.08.2011 16:01 | Nikolai Petrin

Pervaya formula, skorost' puli u celi (m/s), VK = V0*ehr(-0.012 L) vyvoditsya iz tochnogo resheniya uprosheniya uravneniya

dVx/dt= - 0.012*Vx*( Vx^2+Vy^2 )^0.5,

gde vertikal'naya sostavlyayushaya Vy priravnena nulyu (ona deistvitel'no goraaaazdo men'she Vx).
Vtoraya poluchaetsya iz pervoi posle integrirovaniya dt=dx/Vx.

Huzhe s tret'ei formuloi: v nei otsutstvuet nachal'naya skorost'. Avtor formuly ispol'zuet uravnenie dVy/dt = 0.012*Vy^2, "po-shkol'nomu", no s demonstraciei umeniya integrirovat'.
Polnoe ignorirovanie fiziki. Dlya malyh skorostei tam i kvadrata ne dolzhno byt'...

Variant dVu/dt=9.8 - 0.012*Vu*( Vx^2+Vy^2 )^0.5 tochnee sootvestvstvuet modeli kvadratichnoi zavisimosti soprotivleniya ot skorosti.

[Citirovat'][Otvetit'][Novoe soobshenie]

Forumy >> Obsuzhdenie publikacii Astroneta

Spisok / Derevo
Zagolovki / Annotacii / Tekst

Vneshnyaya ballistika pnevmaticheskogo oruzhiya (Astronet, 10.04.2005 23:49, 23.2 KBait, otvetov: 1)

VOT PULYa POLETELA ... VNEShNYaYa BALLISTIKA PNEVMATIChESKOGO ORUZhIYa

V svoe vremya odin kovboi-filosof vyskazal "mudruyu" mysl' o tom, chto kratchaishee rasstoyanie mezhdu nim i cel'yu – eto pulya. Navernoe, on dumal o voobrazhaemoi pryamoi linii, soedinyayushei dulo ego kol'ta 45 kalibra s grud'yu (ili golovoi) svoego protivnika, i eta pryamaya u nego associirovalas' s pulei.

V chem-to kovboi-filosof byl pochti prav, esli uchest', chto svoi otnosheniya s protivnikom on vyyasnyal na maloi distancii – 5...10 m, i v etom sluchae deistvitel'no traektoriyu poleta ego puli mozhno priblizhenno prinyat' kak pryamuyu.

Na samom dele, posle vyleta iz stvola pulya letit ne po pryamoi, a po nekotoroi krivoi, kotoraya i nazyvaetsya ballisticheskoi traektoriei. V bezvozdushnom prostranstve ballisticheskaya traektoriya predstavlyala by soboi parabolu, a vot v vozduhe, kotoryi nas okruzhaet, traektoriya puli pri detal'nom rassmotrenii budet dostatochno slozhnoi, ne raspolagayusheisya v odnoi ploskosti krivoi.

Izucheniem osobennostei dvizheniya pul', snaryadov (da i voobshe lyubyh broshennyh tel) zanimayutsya takie interesnye nauki, kak vneshnyaya ballistika, aerodinamika, mehanika, v chastnosti, takoi ee moshnyi razdel kak dinamika.

Pri polete v atmosfere na pulyu deistvuyut dve osnovnye sily – sila zemnogo prityazheniya i sila soprotivleniya vozduha, a takzhe ryad menee znachimyh sil, naprimer, sila Magnusa, kotoraya v nashem sluchae, t.e. dlya pnevmatiki, chashe proyavlyaetsya pri polete sharoobraznyh pul', poluchivshih nezaplanirovannoe vrashenie v poperechnom napravlenii pri vylete iz stvola), sily aerodinamicheskogo dempfirovaniya (tormozheniya).

Sila prityazheniya vyzyvaet postepennoe snizhenie puli, a sila soprotivleniya vozduha (aerodinamicheskaya sila) nepreryvno umen'shaet skorost' puli i zastavlyaet ee sovershat' v celom dovol'no slozhnoe prostranstvennoe dvizhenie (o chem razgovor poidet dal'she). Na traektoriyu poleta puli takzhe vliyayut i takie faktory, kak meteorologicheskie usloviya (davlenie, vlazhnost' i temperatura vozduha, veter) i nachal'nye vozmusheniya v moment vyleta puli iz stvola.

Ideal'naya traektoriya (pochemu ideal'naya, raz'yasnitsya dalee) poleta puli privedena na ris. 1, s pomosh'yu kotorogo takzhe dostatochno prosto razobrat'sya s terminami, prinyatymi v strelkovom dele.

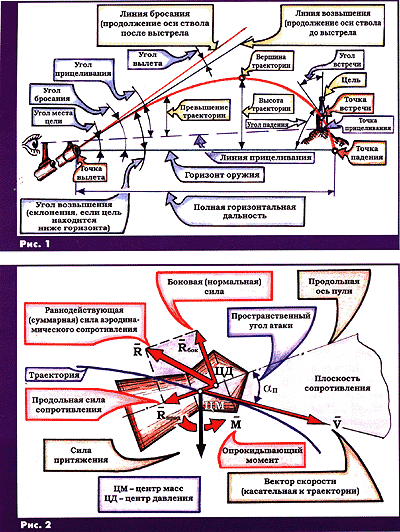K osobennostyam traektorii sleduet otnesti to, chto ee chast' ot vershiny do tochki padeniya (nishodyashaya vetv') koroche i kruche ee chasti ot tochki vyleta do vershiny (voshodyashaya vetv'), a ugol padeniya bol'she ugla brosaniya; ochevidno, chto konechnaya skorost' puli vsegda men'she nachal'noi, i vremya poleta po voshodyashei vetvi traektorii, estestvenno, vsegda men'she, chem po nishodyashei-

A teper', razobravshis' s terminami i opredeleniyami, obratimsya k ris. 2, na kotorom privedena shema osnovnyh sil, deistvuyushih na osesimmetrichnuyu pulyu (v chastnosti, na pnevmaticheskuyu) v polete. V processe poleta mezhdu prodol'noi os'yu puli i kasatel'noi k traektorii (vektorom skorosti V) sushestvuet tak nazyvaemyi prostranstvennyi ugol ataki α_p, obuslovlennyi deistviem na pulyu nachal'nyh vozmushenii pri vystrele, vetra, ponizheniem (otkloneniem vniz) kasatel'noi k traektorii.

Sila gravitacionnogo prityazheniya G prilozhena v centre mass puli i napravlena vniz. Ravnodeistvuyushaya aerodinamicheskaya sila R skladyvaetsya iz sil davleniya vozduha, napravlennyh po normali k poverhnosti puli, i sil treniya vozduha ob etu poverhnost', kasatel'nyh k nei. Silu R, raspolozhennuyu v tak nazyvaemoi ploskosti soprotivleniya (t.e. ploskosti, prohodyashei cherez prodol'nuyu os' puli i vektor skorosti V), mozhno razlozhit' na dve sostavlyayushie. Odna iz nih – prodol'naya sila soprotivleniya R_prod, raspolozhennaya po prodol'noi osi puli v storonu, protivopolozhnuyu ee vershine. Vtoraya – bokovaya (poperechnaya, ili primenitel'no k ris. 2 – normal'naya) sila R_bok, perpendikulyarnaya prodol'noi osi puli i lezhashaya v ploskosti soprotivleniya.

Aerodinamicheskaya sila R prilozhena k pule v tochke, kotoruyu nazyvayut centrom davleniya. Dlya bol'shinstva pnevmaticheskih pul', a takzhe i dlya pul' strelkovogo ognestrel'nogo oruzhiya i artilleriiskih snaryadov centr davleniya ne sovpadaet s centrom mass puli i nahoditsya vperedi nego, t.e. blizhe k vershine. V etom sluchae sila R vyzyvaet aerodinamicheskii moment M, stremyashiisya uvelichit' ugol ataki, t.e. povernut' pulyu vokrug centra mass vershinoi nazad (oprokidyvayushii aerodinamicheskii moment).

Takuyu pulyu nazyvayut staticheski (aerodinamicheski) neustoichivoi. Zametim, chto sushestvuyut i staticheski ustoichivye ballisticheskie ob'ekty, u kotoryh centr davleniya nahoditsya pozadi centra mass, naprimer, drotiki dlya strel'by iz pnevmatiki, "letayushie" shpricy-kanyuli dlya distancionnyh in'ekcii zhivotnym (da inogda i lyudyam), strely dlya luka, volanchiki dlya badmintona i, nakonec, nekotorye krylatye rakety. U etih ob'ektov centr davleniya nahoditsya pozadi centra mass (dlya etogo oni osnashayutsya stabilizatorami – kistochkoi, yubkoi, opereniem i t.p.), i aerodinamicheskii moment stremitsya likvidirovat' voznikshii ugol ataki, t.e. sovmestit' prodol'nuyu os' ob'ekta s vektorom skorosti (stabiliziruyushii aerodinamicheskii moment). Izgotovlyat' staticheski ustoichivye puli ne vsegda vozmozhno, da i ne vsegda celesoobrazno po ballisticheskim soobrazheniyam.

I nakonec, sushestvuyut ob'ekty, kotorye yavlyayutsya staticheski neitral'nymi, naprimer, shar, u kotorogo v ideale centr davleniya nahoditsya v centre mass (v geometricheskom centre).

Tak kak zhe vse-taki obespechit' dvizhenie staticheski neustoichivyh pul' "golovoi vpered", t.e. isklyuchit' ih oprokidyvanie pod deistviem aerodinamicheskih sil i tem samym poluchit' horoshie kuchnost' i tochnost' strel'by? Etogo mozhno dobit'sya, pridav pule bystroe vrashatel'noe dvizhenie vokrug prodol'noi osi (stabilizaciya vrasheniem). Takoe vrashenie mozhno osushestvit' kak s pomosh'yu teh zhe aerodinamicheskih sil (naprimer, v turbinnyh pulyah dlya gladkostvol'nogo oruzhiya), tak i bolee izvestnym dlya nas sposobom – s pomosh'yu special'nyh vintovyh narezov v kanale stvola, kotorye v pnevmaticheskom oruzhii ispol'zuyutsya ochen' chasto, a v ognestrel'nom oruzhii (obychnom i vysokotochnom) – splosh' i ryadom. Dlya bystrovrashayusheisya puli mozhno bez bol'shoi pogreshnosti prinyat', chto ee kineticheskii moment sovpadaet s prodol'noi os'yu i napravlen v storonu ee vershiny pri pravom vrashenii (po chasovoi strelke, esli smotret' s donnoi chasti) i v storonu donnoi chasti pri levom. Primenitel'no k giroskopam (a nasha pulya – otlichnyi giroskop) takoi kineticheskii moment nazyvaetsya sobstvennym kineticheskim momentom (on opredelyaetsya kak proizvedenie uglovoi skorosti vrasheniya na moment inercii puli otnositel'no prodol'noi osi). I vot takoi sobstvennyi kineticheskii moment i "derzhit" pulyu na traektorii, ne davaya ei oprokinut'sya.

Rassmotrim, kak eto proishodit v sluchae puli, kotoraya vyletaet iz stvola "ideal'no", t.e. bez pomeh. V etom sluchae v nachale poleta prodol'naya os' puli sovpadaet s vektorom skorosti (s kasatel'noi k traektorii), t.e. prostranstvennyi ugol ataki raven nulyu. Aerodinamicheskaya sila napravlena po osi puli i prosto tormozit ee. Zatem pod deistviem sily prityazheniya kasatel'naya k traektorii nachinaet ponizhat'sya, i poyavlyaetsya ugol ataki. Aerodinamicheskaya sila R prodolzhaet tormozit' pulyu (sila R_prod) i odnovremenno (sila R_bok) pytaetsya oprokinut' ee (na ris. 2 – povernut' protiv chasovoi strelki vokrug centra mass momentom M). A tak kak pulya obladaet sobstvennym kineticheskim momentom, poyavlyaetsya kompensiruyushii giroskopicheskii moment, ravnyi oprokidyvayushemu momentu M, no napravlennyi v protivopolozhnuyu storonu.

Pulya zhe v sootvetstvii so svoistvami giroskopa nachnet otklonyat'sya ne v storonu deistviya sily, a po napravleniyu, perpendikulyarnomu sile, v dannom sluchae – vpravo. No kak tol'ko vershina puli nachnet dvizhenie vpravo, nachnet izmenyat'sya polozhenie ploskosti soprotivleniya, t.e. i napravlenie deistviya sostavlyayushei aerodinamicheskoi sily R_bok – ona nachnet takzhe deistvovat' pravee. Vershina puli nachnet uhodit' vniz, sila R_bok – takzhe vniz i t.d. V rezul'tate vershina puli opisyvaet okruzhnost', a ee prodol'naya os' – konus s vershinoi v centre mass. Takoe dvizhenie nazyvaetsya precessionnym ili prosto precessiei (ris. 3). Poskol'ku ugol ataki (polurastvor konusa precessii) dostatochno mal, to pulya letit vershinoi vpered. No eto – v ideale, t.e. kak bylo skazano, dlya poleta puli bez nachal'nyh pomeh. Na samom dele v moment vyleta iz stvola, vsledstvie ego vzdragivaniya (naprimer, ot otdachi) i pod ostatochnym deistviem szhatogo gaza (vozduha) pulya poluchaet nekotoryi bokovoi tolchok ili impul's. Napravlenie etogo tolchka, voobshe govorya, mozhet byt' proizvol'nym. Pri etih usloviyah naibolee estestvenno (kak eto i prinyato v strelkovoi i artilleriiskoi praktike) polagat', chto pri vylete iz stvola pulya ot tolchka pochti mgnovenno poluchaet nachal'nuyu uglovuyu skorost' v poperechnom napravlenii. V svyazi s etim (i opyat'-taki v svyazi so svoistvami giroskopa) prodol'naya os' puli nachnet dopolnitel'no sovershat' radial'noe dvizhenie (kolebaniya), nazyvaemoe nutacionnym ili prosto nutaciei.

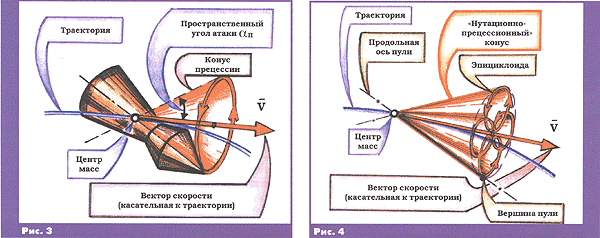
V rezul'tate (ris. 4) vershina puli nachnet opisyvat' dovol'no hitruyu krivuyu, nazyvaemuyu epicikloidoi, a prodol'naya os' puli – ves'ma zamyslovatyi konus s osnovaniem v vide etoi samoi epicikloidy. Nutacionnye kolebaniya postepenno zatuhayut pod deistviem sil aerodinamicheskogo dempfirovaniya.

Estestvenno, na pervyi vzglyad kazhetsya, chto upomyanutye konusy opisyvayutsya prodol'noi os'yu puli vokrug vektora skorosti (t.e. vokrug kasatel'noi k traektorii), chto deistvitel'no i proishodit v samom nachale traektorii. No zatem kasatel'naya k traektorii pod deistviem sily prityazheniya nachinaet ponizhat'sya, i eto privodit k tomu, chto pulya nachinaet kolebat'sya ne otnositel'no vektora skorosti, a otnositel'no tak nazyvaemoi dinamicheskoi osi ravnovesiya, kotoraya otklonena vbok (vpravo pri pravom vrashenii) ot vektora skorosti na nekotoryi ugol. Etot ugol, v chastnosti, pryamo proporcionalen skorosti vrasheniya puli i krutizne traektorii. I vot eto samoe otklonenie vpravo dinamicheskoi osi ravnovesiya ot vektora skorosti privodit k vozniknoveniyu dobavochnogo bokovogo "doveska" k aerodinamicheskoi sile, v rezul'tate proishodit dopolnitel'noe peremeshenie centra mass puli takzhe vpravo. Eto specificheskoe yavlenie nazyvaetsya derivaciei, kotoruyu neobhodimo uchityvat' pri strel'be na bol'shie dal'nosti.

Nu, i esli byt' dostatochno skrupuleznym, sleduet otmetit' sleduyushee. Uglovye precessionno-nutacionnye kolebaniya puli vokrug centra mass privodyat k tomu, chto i sam centr mass odnovremenno s derivacionnym uhodom sovershaet v poperechnoi ploskosti takie zhe kolebaniya, t.e. opisyvaet postepenno zatuhayushuyu epicikloidu.

Takim obrazom, traektoriya puli, kak bylo upomyanuto v nachale stat'i, yavlyaetsya deistvitel'no slozhnoi krivoi: centr mass puli letit vpered i vpravo (derivaciya), sovershaya pri etom poperechnye epicikloidal'nye kolebaniya, a sama pulya sovershaet takie zhe kolebaniya vokrug centra mass. Odnako pust' nas, dorogoi chitatel', eto ne smushaet: vse poperechnye kolebaniya pul' pnevmaticheskogo, da i v osnovnom strelkovogo ognestrel'nogo oruzhiya, kak budet pokazano nizhe, ves'ma i ves'ma maly i k tomu zhe postepenno zatuhayut (eti kolebaniya oshutimy v moshnoi dal'noboinoi artillerii), a derivaciya kompensiruetsya pravil'noi pristrelkoi.

Neobhodimo otmetit' dvoistvennyi harakter deistviya na pulyu oprokidyvayushego momenta ot aerodinamicheskoi sily. S odnoi storony, etot moment obuslovlivaet neobhodimost' pridaniya pule giroskopicheskoi ustoichivosti za schet vrasheniya, chtoby ne dopustit' ee kuvyrkaniya (i ne uhudshit' dal'nost', tochnost' i kuchnost' strel'by). S drugoi storony, na krivolineinom uchastke traektorii vrashayushayasya pulya "sledit" za kasatel'noi k traektorii tol'ko blagodarya tomu, chto na nee deistvuet oprokidyvayushii moment. Esli by ne bylo etogo momenta (ne bylo by vozduha), prodol'naya os' puli (vektor ee sobstvennogo kineticheskogo momenta) pri dvizhenii po traektorii peremeshalas' by ploskoparallel'no i sohranyala by nachal'nuyu orientaciyu v prostranstve, poluchennuyu pri vylete iz stvola (t.e. pulya mogla by popast' v cel' pod bol'shim uglom, a to i voobshe pochti bokom).

My vse vremya govorim o vrashenii puli, i voznikaet estestvennyi vopros, s kakoi uglovoi skorost'yu ee vrashat'. Ne vlezaya v gustye debri mehaniki, aerodinamiki, teorii ustoichivosti otmetim, chto vybor skorosti vrasheniya osushestvlyaetsya po dvum kriteriyam. Pervyi kriterii zadaet nizhnee, dopustimoe dlya obespecheniya ustoichivosti puli, znachenie uglovoi skorosti, ishodya iz sootnoshenii momentov inercii puli otnositel'no prodol'noi i poperechnoi osei, ee nachal'noi skorosti, ploshadi poperechnogo secheniya, rasstoyaniya mezhdu centrom mass i centrom davleniya (plecha aerodinamicheskoi sily), nekotoryh aerodinamicheskih koefficientov. Vtoroi kriterii opredelyaet verhnyuyu granicu skorosti vrasheniya, ishodya iz minimizacii ugla otkloneniya dinamicheskoi osi ravnovesiya ot vektora skorosti: ustoichivaya vrashayushayasya pulya dolzhna "sledit'" za kasatel'noi k traektorii, poetomu dopuskat' bol'shih otklonenii dinamicheskoi osi ne sleduet (t.e. nel'zya chrezmerno uvelichivat' skorost' vrasheniya). Eta granica opredelyaetsya ustoichivym dvizheniem puli v vershine traektorii, t.e. v kriticheskoi tochke, gde nablyudaetsya peregib. Tut vozmozhen kazus – nizhnyaya granica prevoshodit verhnyuyu: eto proishodit pri ochen' bol'shih uglah brosaniya (bol'she 70 grad.), svoistvennyh moshnoi dal'noboinoi artillerii. V etom sluchae prihoditsya iskat' drugie sposoby obespecheniya stabilizacii snaryadov (naprimer, s pomosh'yu opereniya).

Tak kak my strelyaem iz pnevmatiki po ochen' nastil'nym traektoriyam (v bol'shinstve sluchaev s uglami brosaniya menee 10 grad.), to dlya nas "perestabilizaciya" puli vrasheniem ne strashna, osobenno, esli cel' porazhaetsya na voshodyashei vetvi traektorii (a chasto tak i byvaet). Pri etom, poskol'ku dlya kazhdogo kalibra pnevmatiki sushestvuet celaya gamma pul' s raznoi stepen'yu staticheskoi neustoichivosti (kotoraya opredelyaetsya otnosheniem raznosti rasstoyanii ot vershiny puli do centra mass i centra davleniya k ee dline), razbrosom masso-gabaritnyh harakteristik i t.p., firmy-proizvoditeli oruzhiya obychno vypuskayut universal'nye stvoly s povyshennoi krutiznoi narezov dlya garantirovannoi ustoichivosti dazhe samyh neustoichivyh pul'. Poetomu skorost' vrasheniya puli vybiraetsya s dostatochno bol'shim zapasom – na 25...50% bol'she minimal'no dopustimogo znacheniya.

Zadannaya uglovaya skorost' vrasheniya puli obespechivaetsya s pomosh'yu narezov v stvole. Dlina hoda ih ravna lineinoi (dul'noi) skorosti puli, podelennoi na skorost' vrasheniya (uglovuyu skorost') i umnozhennoi na 2π. Esli dlinu hoda narezov podelit' na kalibr stvola, to poluchim dlinu hoda narezov v kalibrah (bolee universal'nyi parametr).

Neobhodimo vkratce upomyanut' o vliyanii na polet puli meteouslovii. Normal'nye meteousloviya -eto temperatura vozduha +15 S, davlenie 750 mm rt. st., vlazhnost' 50%, veter otsutstvuet. Izmenenie meteouslovii napryamuyu vliyaet na plotnost' vozduha, t.e. i na proporcional'nuyu ei aerodinamicheskuyu silu, kotoraya deistvuet na pulyu.

Tak, povyshenie atmosfernogo davleniya, vlazhnosti i ponizhenie temperatury privodit k uvelicheniyu plotnosti vozduha (i, v rezul'tate, k umen'sheniyu dal'nosti poleta puli) i naoborot. Veter vliyaet na polet pul' opyat'-taki cherez tu zhe samuyu aerodinamicheskuyu silu. Esli veter poputnyi ili vstrechnyi, to sootvetstvenno ubyvaet ili vozrastaet prodol'naya sila soprotivleniya, a znachit, vozrastaet ili umen'shaetsya dal'nost' poleta puli.

Bokovoi veter privodit k poyavleniyu dopolnitel'nogo ugla ataki v bokovoi ploskosti, t.e. k vozrastaniyu bokovoi sostavlyayushei aerodinamicheskoi sily i, sootvetstvenno k otkloneniyu puli v tu storonu, kuda duet veter. Primenitel'no k pnevmatike otmetim, chto sil'nyi (skorost' 6...8 m/s) i umerennyi (4...5 m/s) veter sushestvenno vliyaet na legkuyu pulyu, imeyushuyu maluyu poperechnuyu nagruzku (otnoshenie massy puli k ploshadi ee poperechnogo secheniya) i otnositel'no nebol'shuyu skorost'.

Takovy vkratce teoreticheskie osnovy poleta puli. Zdes' my umyshlenno ne govorim o takih razdelah vneshnei ballistiki kak rasseivanie, pristrelka oruzhiya i t.p., tak kak oni dostatochno polno izlozheny v dostupnyh nastavleniyah po strelkovomu delu.

Pogovorim luchshe nemnogo o prakticheskoi storone poleta puli (a to teoreticheskie "zerna" – eto vse izyashnaya slovesnost', a ved' nuzhno chto-to i poklevat').

Rassmotrim tipovuyu pnevmaticheskuyu pulyu tipa "d'yablo" Gamo Hunter kalibra 4,5 mm s kupoloobraznoi golovkoi, obladayushuyu dovol'no vysokoi kuchnost'yu i sohranyayushei maksimum energii na bol'shih dal'nostyah.

Usrednennye dannye po takoi pule sleduyushie: massa ~0,47 g (7,25 gran); dlina ~5,7 mm; diametr golovnoi chasti 4,5 mm, diametr yubki – 4,7 mm; rasstoyanie centra mass ot vershiny ~2,73 mm, a centra davleniya ~2,4 mm (pulya imeet maluyu staticheskuyu neustoichivost' - 5,8%).

Ostal'nymi parametrami (takimi, naprimer, kak momenty inercii puli, ee aerodinamicheskie koefficienty) ne budem peregruzhat' chitatelya, i otvlekat' ego ot glavnogo – uvidet' v cifrah povedenie puli v polete.

Pust' pulya vystrelivaetsya iz kompressionnogo pistoleta mnogorazovoi nakachki Crosman 1377 kalibra 4,5 mm s dlinoi stvola 250 mm i dlinoi hoda pravyh narezov 500 mm. Srednyaya nachal'naya skorost' puli pri 10 nagnetaniyah sostavlyaet okolo 168 m/s. Rassmatrivaemyi stvol soobshaet pule uglovuyu skorost' vrasheniya ~2111 s^-1, t.e. ~336 ob/s. Minimal'naya trebuemaya skorost' dlya takoi puli iz usloviya obespecheniya giroskopicheskoi ustoichivosti sostavlyaet ~1505 s^-1 (240 ob/s), tak chto koefficient zapasa po skorosti vrasheniya dlya nashei puli sostavlyaet primerno 1,4.

Prinimaem, chto pri vylete iz stvola pulya poluchaet dostatochno zhestkie dlya pnevmatiki nachal'nye usloviya – nachal'naya uglovaya skorost' v poperechnom napravlenii sostavlyaet 50 grad/s (razbros nachal'nyh uglovyh skorostei v poperechnom napravlenii dlya strelkovogo oruzhiya sostavlyaet 30...60 grad/s, a v pnevmatike mozhet byt' eshe men'she, v zavisimosti ot tipa oruzhiya, prikladki strelka i t.p.).

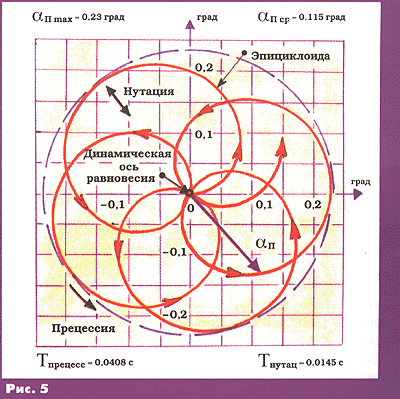Na ris. 5 po rezul'tatam raschetov privedena illyustraciya uglovogo dvizheniya vershiny puli otnositel'no dinamicheskoi osi ravnovesiya v proekcii na poperechnuyu ploskost' (pulya letit na nablyudatelya).

Maksimal'noe znachenie prostranstvennogo ugla ataki pri zadannyh nachal'nyh usloviyah sostavlyaet ~0,23 grad., srednee znachenie ~0,115 grad, (malyusen'kaya velichina, pochti nul'!). Dinamicheskaya os' ravnovesiya otklonyaetsya ot vektora skorosti na maksimal'nyi ugol – 0,043 grad, (nastol'ko malo, chto mozhno schitat', chto pulya kolebletsya vokrug vektora skorosti). Pri etom period precessii sostavlyaet ~ 0,0408 s, a nutacii sootvetstvenno ~0,0145 s. Takim obrazom, nasha (hotya po proishozhdeniyu ispanskaya) pulya sovershaet ves'ma rezvye uglovye kolebaniya po ochen' malen'koi epicikloide, da eshe ochen' bystro krutitsya vokrug prodol'noi osi. Otmetim, chto centr mass puli takzhe opisyvaet v poperechnoi ploskosti mikroskopicheskuyu epicikloidu s maksimal'nym radiusom ~0,05 mm (schitaem, chto nasha pulya letit plavno) i temi zhe vremennymi harakteristikami, chto i u uglovogo dvizheniya. Derivaciya puli pri strel'be na 10 m sostavlyaet vsego okolo 1,8 mm (hotya uzhe est' chto kompensirovat' pri pristrelke!). Chto mozhno skazat' ob etih malyh velichinah? Malen'kaya pulya – i vse ostal'noe malen'koe.

A teper' v zaklyuchenie privedem neskol'ko prostyh priblizhennyh sootnoshenii, pozvolyayushih (esli, konechno, est' interes) "na kolenke" rasschitat' nekotorye osnovnye usrednennye parametry traektorii pri nastil'noi strel'be pulyami tipa "d'yablo" kalibra 4,5 mm s massoi 0,50,1 g. Napomnyu, chto pod "d'yavolom" podrazumevaetsya pulya s yarko vyrazhennoi golovnoi chast'yu lyuboi iz izvestnyh form (ploskaya, kupoloobraznaya, polusfericheskaya ili konusnaya) i "yubkoi" (s nasechkoi ili bez).

Skorost' puli u celi (m/s)	V_K = V₀/e^0.012 L;
Poletnoe vremya (s)	T = (e^0.012 L – 1)/(0,012V₀);
Ponizhenie traektorii pri gorizontal'nom vystrele (m)	δN = 28,9 T + 85 ln [(1 + e^-0.68 T)/2];
Derivaciya (m)	D = 253 ω₀ (e^0.012 L – 1)²/V₀³.

Zdes': V₀ – dul'naya skorost' (m/s); L – dal'nost' strel'by (m); ω₀ – uglovaya skorost' vrasheniya puli vokrug prodol'noi osi (s ).

U nekotoryh chitatelei mozhet poyavit'sya nedoumenie po povodu razmernostei v formulah, no zdes' net oshibki – VSE uchteno v cifrovyh koefficientah.

Takovo kratkoe, ochen' kratkoe, opisanie processa poleta pnevmaticheskoi puli.

(Stat'ya perepechatana iz zhurnala "Pnevmaticheskoe oruzhie v Rossii", N 3, 2003.)

>> Re: Vneshnyaya ballistika pnevmaticheskogo oruzhiya (Nikolai Petrin, 1.08.2011 16:01, 769 Bait)
Pervaya formula, skorost' puli u celi (m/s), VK = V0*ehr(-0.012 L) vyvoditsya iz tochnogo resheniya uprosheniya uravneniya
dVx/dt= - 0.012*Vx*( Vx^2+Vy^2 )^0.5,
gde vertikal'naya sostavlyayushaya Vy priravnena nulyu (ona deistvitel'no goraaaazdo men'she Vx).
Vtoraya poluchaetsya iz pervoi posle integrirovaniya dt=dx/Vx.

Huzhe s tret'ei formuloi: v nei otsutstvuet nachal'naya skorost'. Avtor formuly ispol'zuet uravnenie dVy/dt = 0.012*Vy^2, "po-shkol'nomu", no s demonstraciei umeniya integrirovat'.
Polnoe ignorirovanie fiziki. Dlya malyh skorostei tam i kvadrata ne dolzhno byt'...
Variant dVu/dt=9.8 - 0.012*Vu*( Vx^2+Vy^2 )^0.5 tochnee sootvestvstvuet modeli kvadratichnoi zavisimosti soprotivleniya ot skorosti.