args[0]=message
args[1]=DB::DB::Message=HASH(0x2bd57c0)
Re: Chernaya dyra
29.07.2012 21:38 | A.P. Vasi
V.A.Aksenova
Uvazhaemaya prochtite eshe raz vnimatel'no chto ya napisal zdes'
Nachinaya s Re: Chernaya dyra 27.07.201220:32
Eto vse dlya Vas
kratko o bol'shom vzryve chernyh dyrah i rasshirenii.
Vot naprimer ya privel otryvok razgovora na forume.
Vy vnikaite, - zdes' otvetov bol'she na Vashi voprosy
chem v knizhkah po dvesti stranic.
---
\\\
.... Material iz Vikipedii Rentgenovskie trubki
Rentgenovskie luchi voznikayut pri sil'nom uskorenii
zaryazhennyh chastic (tormoznoe izluchenie), libo pri
vysokoenergeticheskih perehodah v elektronnyh obolochkah
atomov ili molekul. Oba effekta ispol'zuyutsya v
rentgenovskih trubkah.....
A rentgenovskoe izluchenie est' - sledovatel'no
ego istochnikom mozhet byt' tol'ko rezul'tat yadernoi
reakcii.
....Material iz Vikipedii
Gámma-izluchénie
gamma-izluchenie i rentgenovskoe izluchenie razlichayutsya tol'ko po istochniku:
esli kvant izluchaetsya v yadernom perehode, to ego prinyato otnosit' k
gamma-izlucheniyu; esli pri vzaimodeistviyah elektronov ili pri perehodah
v atomnoi elektronnoi obolochke k rentgenovskomu izlucheniyu.....
A esli rezul'tat izlucheniya istochnik yadernoi reakcii -
i on dlitsya godami, - to eto neitronnaya zvezda.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Uvazhaemyi
Dmitrii Mamontov
Moe - A gospodin A.M.ChEREPAShUK, v Vashei ssylke, ya tak ponyal reshil - zachem dobru propadat' - pust' izluchenie ( Izluchénie Hókinga) iz chernoi dyry budet eshe i preimushestvenno iz rentgenovskih chastic.
Vashe - Rentgenovskoe izluchenie ChD voznikaet pri akkrecii veshestva. Izluchenie Hokinga - drugoi process. Stranno, chto za 7 let "uvlecheniya astrofizikoi" Vy etogo ne ponyali.
Moe - S moei tochki zreniya - uvazhaemyi A.M.ChEREPAShUK imeet takoe zhe otnoshenie
k Chernym Dyram kak ya ili Vy.
My s Vami, i A.M.ChEREPAShUK mozhem tol'ko predpolagat' i vyskazyvat'
svoyu tochku zreniya, no obrashat' vnimaniya na podobnye vyskazyvaniya i brat'
ih na veru, ya ne vizhu smysla.
Drugoe delo avtor. Kak on skazal to - takie i Chernye Dyry.
Uvazhaemyi
Dmitrii Mamontov
Vot ya naprimer govoryu chto veshestvo padaet na chernuyu dyru,
i posle udara o poverhnost' s protivopolozhnoi storony chernoi dyry voznikaet rentgenovskoe i svetovoe izluchenie.
Drugoi schitaet chto izluchenie na podlete.
V binokl' ne vidno - odni predpolozheniya, i ih mozhet byt'
bol'she sotni naprimer - komu verit'?
Uvazhaemyi
Dmitrii Mamontov
Vy zatragivaete vopros interpretacii avtorskih
idei bez soglasiya s avtorom.
A esli desyatok drugih avtorov opublikuyut po 300 nauchnyh rabot, a avtor o Chernyh Dyrah govorit chto izluchenie v osnovnom iz fotonov - a vse drugie govoryat, chto
izluchenie iz rentgenovskih chastic, drugoi govorit iz radio izlucheniya, a tretii govorit iz gamma chastic - ya dolzhen slushat' isklyuchitel'no avtora Chernyh Dyr,
a ne teh kto interpretiruet, i tem bolee teh kto plevat' hotel na avtorskii variant chernyh dyr.
Nikto ne meshaet pridumat' svoi - rentgenovskie chernye dyry, - tak net ne hotyat, - tak na neudobnye voprosy otvechat' dolzhen budet avtor, a pri interpretacii avtora - pisaka naprimer stat'i s levymi ideyami v oblasti Chernyh Dyr, prikryvaetsya avtorstvom avtora
Chernyh Dyr, a sam so svoim bredom po otnosheniyu k avtorskomu izlozheniyu, kak-by i ne prichem.
Uvazhaemyi
Dmitrii Mamontov
..Material iz Vikipedii
Izluchénie Hókinga process ispuskaniya
raznoobraznyh elementarnyh chastic,
preimushestvenno fotonov, chernoi dyroi....
\\\
Sergei Popov - Tanec Chernyh Dyr :-) - YouTube
[Citirovat'][Otvetit'][Novoe soobshenie]
| Forumy >> Obsuzhdenie publikacii Astroneta |
| Spisok / Derevo Zagolovki / Annotacii / Tekst |
- Chernaya dyra
(I. D. Novikov, "Fizika Kosmosa", 1986,
26.03.2003 20:16, 22.4 KBait, otvetov: 659)
1. Vvedenie
2. Pole tyagoteniya nevrashayusheisya chernoi dyry
3. Pole tyagoteniya vrashayusheisya chernoi dyry
4. Fizicheskie processy v pole tyagoteniya chernoi dyry1. Vvedenie
Chernaya dyra - oblast' prostranstva, v k-roi pole tyagoteniya nastol'ko sil'no, chto vtoraya kosmich. skorost' (parabolicheskaya skorost') dlya nahodyashihsya v etoi oblasti tel dolzhna byla by prevyshat' skorost' sveta, t.e. iz Ch.d. nichto ne mozhet vyletet' - ni izluchenie, ni chasticy, ibo v prirode nichto ne mozhet dvigat'sya so skorost'yu, bol'shei skorosti sveta. Granicu oblasti, za k-ruyu ne vyhodit svet, naz. gorizontom Ch.d. Dlya togo chtoby pole tyagoteniya smoglo "zaperet'" izluchenie, sozdayushee eto pole massa
 dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa
dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa 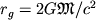 . Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu
. Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu 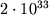 g,
g, 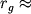 3 km).
3 km).
Pole tyagoteniya Ch.d. opisyvaetsya teoriei tyagoteniya Einshteina (sm. Tyagotenie). Soglasno etoi teorii, vblizi Ch.d. geometrich. sv-va prostranstva opisyvayutsya neevklidovoi (rimanovoi) geometriei, a vremya techet medlennee, chem vdali, vne sil'nogo polya tyagoteniya.
Po sovr. predstavleniyam, massivnye zvezdy (s massoi v nesk.
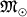 i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
Esli Ch.d. voznikaet pri szhatii nevrashayushegosya nezaryazhennogo tela, to ee vnesh. pole tyagoteniya okazyvaetsya strogo sfericheskim i zavisyashim tol'ko ot polnoi massy tela
 . Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
. Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
Pri obrazovanii Ch.d. izluchayutsya takzhe vse fiz. polya, krome staticheskogo elektricheskogo polya (esli kollapsiruyushee telo bylo elektricheski zaryazhennym).
Esli telo, obrazovavshee Ch.d., vrashalos', to vokrug Ch.d. sohranyaetsya "vihrevoe" gravitac. pole, uvlekayushee vse tela vblizi Ch.d. vo vrashatel'noe dvizhenie vokrug nee. Eto pole opredelyaetsya pomimo massy Ch.d. tol'ko ee polnym momentom impul'sa. Pole tyagoteniya vrashayusheisya Ch.d. naz. polem Kerra.
2. Pole tyagoteniya nevrashayusheisya chernoi dyry
Dvizhenie tel v pole tyagoteniya Shvarcshil'da obladaet ryadom osobennostei. V teorii N'yutona dvizhenie po okruzhnosti vokrug tyagoteyushego centra vozmozhno na lyubom rasstoyanii R ot nego. V teorii Einshteina eto ne tak. Chem blizhe k Ch.d., tem bol'she skorost' krugovogo dvizheniya. Na okruzhnosti s R=1,5 rg skorost' dvizheniya dostigaet svetovoi. Blizhe k Ch.d. dvizhenie po okruzhnosti, ochevidno, voobshe nevozmozhno. V deistvitel'nosti zhe dvizhenie po okruzhnosti stanovitsya neustoichivym na znachitel'no bol'shih rasstoyaniyah, a imenno: nachinaya s R=3 rg, kogda skorost' dvizheniya sostavlyaet vsego polovinu svetovoi. Tol'ko na rasstoyaniyah, prevyshayushih 3rg, vozmozhno ustoichivoe krugovoe dvizhenie. Na predele ustoichivosti krugovyh orbit energiya svyazi chasticy
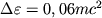 , gde m - massa
chasticy.
, gde m - massa
chasticy.
Osobyi interes predstavlyaet vozmozhnost' gravitac. zahvata chernoi dyroi tel, priletayushih iz beskonechnosti k tyagoteyushei masse, opisyvaet okolo nee parabolu ili giperbolu i (esli ne ispytyvaet soudareniya s tyagoteyushei massoi) snova uletaet v beskonechnost'. Gravitac. zahvat v etoi zadache nevozmozhen.
Inache obstoit delo v pole tyagoteniya Ch.d. Konechno, esli telo dvizhetsya na bol'shih rasstoyaniyah ot Ch.d. (R>rg), gde pole tyagoteniya uzhe slabo i spravedliva s bol'shoi tochnost'yu teoriya N'yutona, to traektoriya dvizheniya pochti tochno sovpadaet s paraboloi ili giperboloi. V dostatochnoi blizosti ot Ch.d. traektoriya rezko otlichaetsya ot n'yutonovskoi. Tak, esli skorost' tela vdali ot Ch.d. mnogo men'shn svetovoi i traektoriya ego dvizheniya podhodit blizko k okruzhnosti s R=2 rg, to telo sovershit mnogo oborotov vokrug Ch.d., prezhde chem snova uletit v kosmos (ris. 1, a).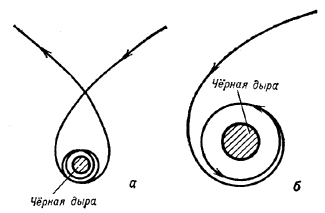
Ris. 1. Nakonec, esli telo podoidet vplotnuyu k ukazannoi okruzhnosti, to ego orbita budet neogranichenno navivats'ya na okruzhnost'. Telo okazhetsya gravitacionno zahvachennym Ch.d. i nikogda snova ne uletit v kosmos (ris. 1, b). Esli zhe telo podletit eshe blizhe k Ch.d., to posle nesk. oborotov ili dazhe ne uspev sdelat' ni odnogo oborota, ono upadet v Ch.d.
V pole tyagoteniya Ch.d. vyrazhenie dlya parabolicheskoi skorosti zapisyvaetsya formal'no tak zhe, kak i v teorii N'yutona. Odnako neobhodimo sdelat' sleduyushee utochnenie. Kogda telo dvizhetsya pryamo po radisu k Ch.d., to kakuyu by skorost' telo ne imelo, v t.ch. i bol'she parabolicheskoi, ono upadet v Ch.d. Bolee togo, esli telo dvizhetsya hotya i ne pryamo po radiusu k Ch.d., no traektoriya ego dostatochno blizka k Ch.d., to ono tozhe budet zahvacheno Ch.d. Sledovatel'no, dlya togo chtoby vyrvat'sya iz okrestnostei Ch.d., malo imet' skorost', prevyshayushuyu parabolicheskuyu, nado eshe, chtoby ugol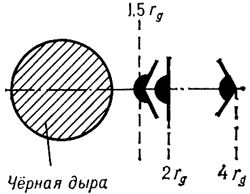
Ris. 2. 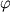 mezhdu napravleniem etoi
skorosti i napravleniem na Ch.d. prevyshal nek-roe kritich. znachenie
mezhdu napravleniem etoi
skorosti i napravleniem na Ch.d. prevyshal nek-roe kritich. znachenie 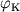 .
Pri
.
Pri 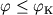 telo okazhetsya zahvachennym Ch.d., pri
telo okazhetsya zahvachennym Ch.d., pri 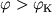 (i uslovii, chto skorost' bol'she ili ravna parabolicheskoi) telo uletit
ot Ch.d. Znachenie
(i uslovii, chto skorost' bol'she ili ravna parabolicheskoi) telo uletit
ot Ch.d. Znachenie 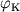 zavisit ot rasstoyaniya do Ch.d. Na ris. 2 chernym
cvetom zakrashen konus zahvata: esli vektor parabolicheskoi skorosti raspolagaetsya
v etom
konuse, to telo budet zahvacheno Ch.d.
zavisit ot rasstoyaniya do Ch.d. Na ris. 2 chernym
cvetom zakrashen konus zahvata: esli vektor parabolicheskoi skorosti raspolagaetsya
v etom
konuse, to telo budet zahvacheno Ch.d.
Pole tyagoteniya Ch.d. iskrivlyaet traektorii luchei sveta (i voobshe lyubyh ul'trarelyativistskih chastic, k-rye dvizhutsya prakticheski po tem zhe traektoriyam, chto i fotony). Chem blizhe k Ch.d. traektorii, tem sil'nee oni iskrivleny. Na ris. 3, a privedeny traektorii luchei sveta, ispushennyh na raznyh rasstoyaniyah ot Ch.d. perpendikulyarno k radial'nomu napravleniyu. Dlya luchei sushestvuet kritich. okruzhnost' s R=1,5 rg. Po etoi okruzhnosti mozhet dvigat'sya foton, uderzhivaemyi tyagoteniem Ch.d. Odnako eto dvizhenie neustoichivo. Pri maleishem vozmushenii foton libo popadaet v Ch.d., libo uletaet v kosmos.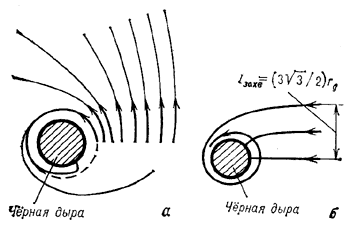
Ris. 3. Nalichie kritich. okruzhnosti vedet k tomu, chto vse luchi s pricel'nym parametrom na beskonechnosti
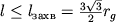 gravitacionno zahvatyvayutsya
(ris. 3, b).
gravitacionno zahvatyvayutsya
(ris. 3, b).
3. Pole tyagoteniya vrashayusheisya chernoi dyry
Okolo vrashayusheisya Ch.d., kak uzhe bylo skazano, dolzhno sushestvovat' "vihrevoe" gravitac. pole. Vdali ot Ch.d. ono ochen' slabo, a vblizi vozrastaet nastol'ko, chto vedet k kachestvenno novym effektam.
Tak, v okrestnosti vrashayusheisya Ch.d. voznikaet oblast', v k-roi vse tela i fotony uvlekatsya v dvizhenie vokurg Ch.d. Vnesh. granica etoi oblasti naz. predelom statichnosti. Odnako vnutri predela statichnosti tela i fotony sovsem ne obyazatel'no dolzhny padat' k centru, oni mogut i priblizhat'sya k Ch.d. i udalyat'sya ot nee, mogut vyhodit' za predel statichnosti. T.o., predel statichnosti ne yavl. granicei Ch.d., ee gorizontom, iz-pod k-rogo nel'zya vyiti. Lineinye razmery predela statichnosti po poryadku velichiny ravny rg. Gorizont Ch.d. raspolozhen glubzhe, pod predelom statichnosti. Prostranstvo mezhdu gorizontom i predelom statichnosti naz. ergosferoi (ris. 4). Predel statichnosti kasaetsya gorizonta v polyusah vrashayusheisya Ch.d.
Pri padenii tela na vrashayushuyusya Ch.d. ono snachala otklonyaetsya v svoem dvizhenii v storonu vrasheniya Ch.d., peresekaet granicu ergosfery i postepenno priblizhaetsya k gorizontu. Dlya vnesh. nablyudatelya svet, ispuskaemyi padayushim telom, stanovitsya vse bolee krasnym i menee intensivnym, zatem polnost'yu zatuhaet: telo, uidya pod gorizont, stanovitsya nevidimym dlya vnesh. nablyudatelya. Na gorizonte vse tela imeyut odnu tu zhe uglovuyu skorost' obrasheniya, v kakoe by mesto gorizonta ni popadalo padayushee telo.
Obshaya dlya vseh padayushih tel uglovaya skorost'
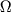 na gorizonte Ch.d.
i est' skorost' ee vrasheniya:
na gorizonte Ch.d.
i est' skorost' ee vrasheniya: 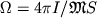 , gde I
-
moment impul'sa tela, iz k-rogo voznikla Ch.d.,
, gde I
-
moment impul'sa tela, iz k-rogo voznikla Ch.d.,  - massa,
S - ploshad' gorizonta Ch.d. Moment impul'sa Ch.d. zadannoi massy ne mozhet byt'
skol'
ugodno bol'shim. Maksimal'no vozmozhnye znacheniya I i
- massa,
S - ploshad' gorizonta Ch.d. Moment impul'sa Ch.d. zadannoi massy ne mozhet byt'
skol'
ugodno bol'shim. Maksimal'no vozmozhnye znacheniya I i 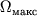 opredelyayutsya tem, chto pri obrazovanii Ch.d. lineinaya skorost' vrasheniya tochek ekvatora
tela
ne prevyshaet skorosti sveta. Po poryadku velichiny
opredelyayutsya tem, chto pri obrazovanii Ch.d. lineinaya skorost' vrasheniya tochek ekvatora
tela
ne prevyshaet skorosti sveta. Po poryadku velichiny 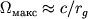 .
Dlya Ch.d. s massoi, ravnoi masse Solnca,
.
Dlya Ch.d. s massoi, ravnoi masse Solnca, 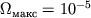 (1/s).
(1/s).
Gravitac. zahvat chastic Ch.d. s vrasheniem neskol'ko otlichaetsya ot zahvata nevrashayusheisya Ch.d. Legche vsego zahvatyvayutsya chasticy, k-rye proletayut vblizi Ch.d. v storonu, protivopolozhnuyu vrasheniyu, trudnee zahvatyvayutsya chasticy, letyashie mimo Ch.d. v storonu vrasheniya. Naglyadno mozhno sebe predstavit', chto vihrevoe gravitac. pole vokrug Ch.d. deistvuet podobno prashe, uskoryaya, otbrasyvaya tem samym chasticy, dvizhushiesya mimo Ch.d. v tu zhe storonu, v k-ruyu zakruchivaetsya "vihr'" etogo polya, i, naoborot, tormozya i zahvatyvaya chasticy, dvizhushiesya protiv "vihrya".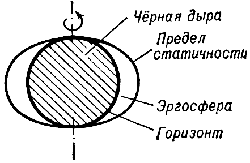
Ris. 4. Rassmotrim dlya primera zahvat fotona, dvizhushegosya v ploskosti ekvatora maksimal'no bystro vrashayusheisya Ch.d.
Dlya fotona, dvizhushegosya v napravlenii vrasheniya Ch.d., pricel'nyi parametr lzahv,1=1/2 rg; dlya fotona, dvizhushegosya protiv vrasheniya, pricel'nyi parametr namnogo bol'she: lzahv,2=4 rg. Izmenyaetsya situaciya i s krugovymi orbitami. Dlya Ch.d. bez vrasheniya poslednyaya ustoichivaya krugovaya orbita imeet radius 3rg; chastica, dvizhushayasya po nei, imeet skorost' c/2. I samoe vazhnoe: chtoby popast' na etu orbitu, chastica s massoi m dolzhna otdat' energiyu
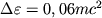 (energiyu svyazi) v vide, napr., gravitacionnogo
izlucheniya.
(energiyu svyazi) v vide, napr., gravitacionnogo
izlucheniya.
V sluchae maksimal'no bystro vrashayusheisya dyry poslednyaya krugovaya orbita lezhit v ekvatorial'noi ploskosti blizko k gorizontu, gluboko vnutri ergosfery. No zdes' chastica mozhet dvigat'sya tol'ko v storonu vrasheniya Ch.d. Energiya, k-ruyu vydelyaet chastica, popavshaya na etu orbitu, gorazdo bol'she i sostavlyaet
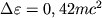 .
V to
zhe vremya poslednyaya ustoichivaya orbita chasticy, obrashayusheisya vokrug dyry v protivopolozhnom
napravlenii, lezhit vne ergosfery i chastica, popadayushaya v nee, vydelyaet energiyu
.
V to
zhe vremya poslednyaya ustoichivaya orbita chasticy, obrashayusheisya vokrug dyry v protivopolozhnom
napravlenii, lezhit vne ergosfery i chastica, popadayushaya v nee, vydelyaet energiyu 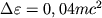 .
.
Polnaya massa vrashayusheisya Ch.d. opredelyaetsya kak ee razmerami (ploshad'yu S gorizonta), tak i energiei vrasheniya:
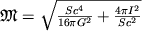 .
.
Esli vrashenie otsutstvuet (I=0), to
 opredelyaetsya
tol'ko razmerami Ch.d. Pri maksimal'no vozmozhnoi skorosti vrasheniya Ch.d. vtoroe slagaemoe
pod kornem ravno pervomu.
opredelyaetsya
tol'ko razmerami Ch.d. Pri maksimal'no vozmozhnoi skorosti vrasheniya Ch.d. vtoroe slagaemoe
pod kornem ravno pervomu.
4. Fizicheskie processy v pole tyagoteniya chernoi dyry
V ergosfere Ch.d. vozmozhny processy, privodyashie k umen'sheniyu energii vrasheniya Ch.d., t.e., kak okazyvaetsya, Ch.d. mozhet teryat' energiyu. V chastnosti, kogda v ergosferu vletae chastica, imevshaya vdali ot Ch.d. energiyu