args[0]=message
args[1]=DB::DB::Message=HASH(0x26933e0)
Re: Chernaya dyra
31.03.2013 18:41 | A.P. Vasi
Takoe prochital, ya azh zaulybalsya u menya poyavilsya
konkurent v opisanii stroeniya galaktik.
Estestvenno tovarishu nado srazu rabotat' nad svoimi
oshibkami, a vsem zhelayushim mogu pokazat'
dve raznyh tochki zreniya i kak govoritsya
pochuvstvuite raznicu.
--------------------------------------
[Citirovat'][Otvetit'][Novoe soobshenie]
| Forumy >> Obsuzhdenie publikacii Astroneta |
| Spisok / Derevo Zagolovki / Annotacii / Tekst |
- Chernaya dyra
(I. D. Novikov, "Fizika Kosmosa", 1986,
26.03.2003 19:16, 22.4 KBait, otvetov: 659)
1. Vvedenie
2. Pole tyagoteniya nevrashayusheisya chernoi dyry
3. Pole tyagoteniya vrashayusheisya chernoi dyry
4. Fizicheskie processy v pole tyagoteniya chernoi dyry1. Vvedenie
Chernaya dyra - oblast' prostranstva, v k-roi pole tyagoteniya nastol'ko sil'no, chto vtoraya kosmich. skorost' (parabolicheskaya skorost') dlya nahodyashihsya v etoi oblasti tel dolzhna byla by prevyshat' skorost' sveta, t.e. iz Ch.d. nichto ne mozhet vyletet' - ni izluchenie, ni chasticy, ibo v prirode nichto ne mozhet dvigat'sya so skorost'yu, bol'shei skorosti sveta. Granicu oblasti, za k-ruyu ne vyhodit svet, naz. gorizontom Ch.d. Dlya togo chtoby pole tyagoteniya smoglo "zaperet'" izluchenie, sozdayushee eto pole massa
 dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa
dolzhna szhat'sya do ob'ema s radiusom,
men'shim gravitacionnogo radiusa 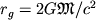 . Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu
. Gravitac. radius chrezvychaino mal dazhe dlya bol'shih mass (napr., dlya
Solnca, imeyushego massu 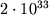 g,
g, 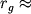 3 km).
3 km).
Pole tyagoteniya Ch.d. opisyvaetsya teoriei tyagoteniya Einshteina (sm. Tyagotenie). Soglasno etoi teorii, vblizi Ch.d. geometrich. sv-va prostranstva opisyvayutsya neevklidovoi (rimanovoi) geometriei, a vremya techet medlennee, chem vdali, vne sil'nogo polya tyagoteniya.
Po sovr. predstavleniyam, massivnye zvezdy (s massoi v nesk.
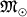 i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
i bol'she), zakanchivaya svoyu evolyuciyu, mogut v konce koncov szhat'sya (skollapsirovat')
i prevratit'sya v Ch.d. (sm. Evolyuciya zvezd,
Gravitacionnyi kollaps).
Esli Ch.d. voznikaet pri szhatii nevrashayushegosya nezaryazhennogo tela, to ee vnesh. pole tyagoteniya okazyvaetsya strogo sfericheskim i zavisyashim tol'ko ot polnoi massy tela
 . Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
. Vse otkloneniya ot sferichnosti v graivtac. pole pri obrazovanii Ch.d. izluchayutsya
v vide gravitac. voln (sm. Gravitacionnoe
izluchenie). Ostavsheesya pole ne zavisit ot raspredeleniya massy vnutri szhavshegosya
tela. T.o., hotya vnutri Ch.d. mozhet byt' "spryatano" ochen' nesimmetrichno szhimayusheesya
telo,
vnesh. pole tyagoteniya budet strogo sfericheski-simmetrichnym (t.n. pole Shvarcshil'da).
Pri obrazovanii Ch.d. izluchayutsya takzhe vse fiz. polya, krome staticheskogo elektricheskogo polya (esli kollapsiruyushee telo bylo elektricheski zaryazhennym).
Esli telo, obrazovavshee Ch.d., vrashalos', to vokrug Ch.d. sohranyaetsya "vihrevoe" gravitac. pole, uvlekayushee vse tela vblizi Ch.d. vo vrashatel'noe dvizhenie vokrug nee. Eto pole opredelyaetsya pomimo massy Ch.d. tol'ko ee polnym momentom impul'sa. Pole tyagoteniya vrashayusheisya Ch.d. naz. polem Kerra.
2. Pole tyagoteniya nevrashayusheisya chernoi dyry
Dvizhenie tel v pole tyagoteniya Shvarcshil'da obladaet ryadom osobennostei. V teorii N'yutona dvizhenie po okruzhnosti vokrug tyagoteyushego centra vozmozhno na lyubom rasstoyanii R ot nego. V teorii Einshteina eto ne tak. Chem blizhe k Ch.d., tem bol'she skorost' krugovogo dvizheniya. Na okruzhnosti s R=1,5 rg skorost' dvizheniya dostigaet svetovoi. Blizhe k Ch.d. dvizhenie po okruzhnosti, ochevidno, voobshe nevozmozhno. V deistvitel'nosti zhe dvizhenie po okruzhnosti stanovitsya neustoichivym na znachitel'no bol'shih rasstoyaniyah, a imenno: nachinaya s R=3 rg, kogda skorost' dvizheniya sostavlyaet vsego polovinu svetovoi. Tol'ko na rasstoyaniyah, prevyshayushih 3rg, vozmozhno ustoichivoe krugovoe dvizhenie. Na predele ustoichivosti krugovyh orbit energiya svyazi chasticy
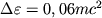 , gde m - massa
chasticy.
, gde m - massa
chasticy.
Osobyi interes predstavlyaet vozmozhnost' gravitac. zahvata chernoi dyroi tel, priletayushih iz beskonechnosti k tyagoteyushei masse, opisyvaet okolo nee parabolu ili giperbolu i (esli ne ispytyvaet soudareniya s tyagoteyushei massoi) snova uletaet v beskonechnost'. Gravitac. zahvat v etoi zadache nevozmozhen.
Inache obstoit delo v pole tyagoteniya Ch.d. Konechno, esli telo dvizhetsya na bol'shih rasstoyaniyah ot Ch.d. (R>rg), gde pole tyagoteniya uzhe slabo i spravedliva s bol'shoi tochnost'yu teoriya N'yutona, to traektoriya dvizheniya pochti tochno sovpadaet s paraboloi ili giperboloi. V dostatochnoi blizosti ot Ch.d. traektoriya rezko otlichaetsya ot n'yutonovskoi. Tak, esli skorost' tela vdali ot Ch.d. mnogo men'shn svetovoi i traektoriya ego dvizheniya podhodit blizko k okruzhnosti s R=2 rg, to telo sovershit mnogo oborotov vokrug Ch.d., prezhde chem snova uletit v kosmos (ris. 1, a).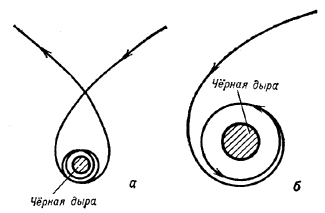
Ris. 1. Nakonec, esli telo podoidet vplotnuyu k ukazannoi okruzhnosti, to ego orbita budet neogranichenno navivats'ya na okruzhnost'. Telo okazhetsya gravitacionno zahvachennym Ch.d. i nikogda snova ne uletit v kosmos (ris. 1, b). Esli zhe telo podletit eshe blizhe k Ch.d., to posle nesk. oborotov ili dazhe ne uspev sdelat' ni odnogo oborota, ono upadet v Ch.d.
V pole tyagoteniya Ch.d. vyrazhenie dlya parabolicheskoi skorosti zapisyvaetsya formal'no tak zhe, kak i v teorii N'yutona. Odnako neobhodimo sdelat' sleduyushee utochnenie. Kogda telo dvizhetsya pryamo po radisu k Ch.d., to kakuyu by skorost' telo ne imelo, v t.ch. i bol'she parabolicheskoi, ono upadet v Ch.d. Bolee togo, esli telo dvizhetsya hotya i ne pryamo po radiusu k Ch.d., no traektoriya ego dostatochno blizka k Ch.d., to ono tozhe budet zahvacheno Ch.d. Sledovatel'no, dlya togo chtoby vyrvat'sya iz okrestnostei Ch.d., malo imet' skorost', prevyshayushuyu parabolicheskuyu, nado eshe, chtoby ugol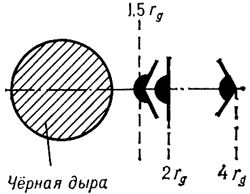
Ris. 2. 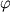 mezhdu napravleniem etoi
skorosti i napravleniem na Ch.d. prevyshal nek-roe kritich. znachenie
mezhdu napravleniem etoi
skorosti i napravleniem na Ch.d. prevyshal nek-roe kritich. znachenie














