<< 5. Standartnye modeli diskovyh | Oglavlenie | 5.2 Vertikal'naya struktura diskov >>
5.1 Radial'noe raspredelenie poverhnostnoi yarkosti
Sglazhennoe radial'noe raspredelenie poverhnostnoi yarkosti v diskah
spiral'nyh galaktik obychno approksimiruetsya
eksponencial'nym zakonom [12,13,39]:
gde
Svetimost', izluchaemaya v predelah rasstoyaniya ![]() ot centra, ravna
ot centra, ravna
(Formuly (45-46) yavlyayutsya chastnymi sluchayami formul (27-28) pri
| (47) |
Krivaya otnositel'noi svetimosti eksponencial'nogo diska, sledovatel'no,
mozhet byt' zapisana tak:
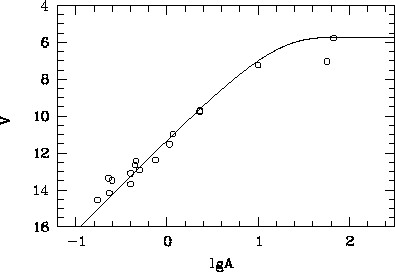 |
Na ris. 19 pokazany rezul'taty aperturnoi fotometrii
blizkoi spiral'noi galaktiki pozdnego (Scd) morfologicheskogo tipa M 33
(tumannost' Treugol'nika) soglasno dannym, privedennym v knige
Sharova [109] i v kataloge [50].
Rezul'taty izmerenii udovletvoritel'no soglasuyutsya s
krivoi otnositel'noi svetimosti dlya eksponencial'nogo diska
pri ![]() i
i ![]() 5.
5.
Esli eksponencial'nyi disk viden v polozhenii ''s rebra'' (![]() )
i yavlyaetsya ''prozrachnym'', to raspredelenie yarkosti vdol' ego
bol'shoi osi vyrazhaetsya kak
)
i yavlyaetsya ''prozrachnym'', to raspredelenie yarkosti vdol' ego
bol'shoi osi vyrazhaetsya kak
| (50) |
Dannye nablyudenii (naprimer, [110]) svidetel'stvuyut o tom, chto
vdali ot centra pri
![]() opticheskie diski
galaktik demonstriruyut rezkoe padenie poverhnostnoi yarkosti, ''obryv''.
opticheskie diski
galaktik demonstriruyut rezkoe padenie poverhnostnoi yarkosti, ''obryv''.
Krivaya vrasheniya beskonechno tonkogo diska s eksponencial'nym raspredeleniem
poverhnostnoi plotnosti
![]() :
:
gde
 |
Real'nye zvezdnye diski galaktik ne yavlyayutsya beskonechno tonkimi,
a imeyut konechnuyu tolshinu. Uchet tolshiny eksponencial'nogo diska
umen'shaet ego maksimal'nuyu skorost' vrasheniya. V stat'e [94]
dlya predstavleniya krivoi vrasheniya diska ispol'zuetsya, kak eto bylo sdelano
dlya galaktiki, opisyvaemoi zakonom Vokulera, formula (23)
(sm. p. 4.1.2), v kotoroi ![]() -- effektivnyi radius eksponencial'nogo
diska (1.678
-- effektivnyi radius eksponencial'nogo
diska (1.678![]() ), a
), a ![]() -- sootvetstvuyushaya effektivnaya poverhnostnaya
yarkost' (
-- sootvetstvuyushaya effektivnaya poverhnostnaya
yarkost' (![]() ). Bezrazmernaya funkciya
). Bezrazmernaya funkciya
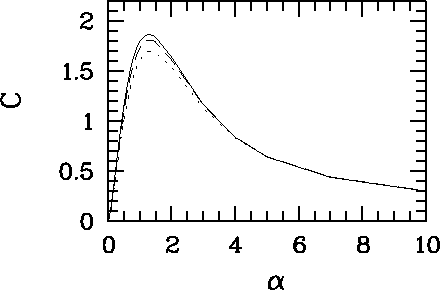
![]() (
(
![]() ), opredelyayushaya formu krivoi vrasheniya,
pokazana na ris. 20 dlya treh znachenii szhatiya
), opredelyayushaya formu krivoi vrasheniya,
pokazana na ris. 20 dlya treh znachenii szhatiya
![]() .
Izmenenie szhatiya diska ot 0.05 do 0.2 privodit k umen'sheniyu
znacheniya
.
Izmenenie szhatiya diska ot 0.05 do 0.2 privodit k umen'sheniyu
znacheniya ![]() na
na ![]() 10%. Maksimum krivoi vrasheniya
dostigaetsya pri
10%. Maksimum krivoi vrasheniya
dostigaetsya pri
![]() ,
V
,
V
![]() (km/s).
(km/s).
Otmechennyi vyshe ''obryv'' zvezdnyh diskov galaktik pri
![]() privodit k tomu, chto pri priblizhenii k
privodit k tomu, chto pri priblizhenii k ![]() krivaya vrasheniya
neskol'ko vozrastaet, a zatem pri
krivaya vrasheniya
neskol'ko vozrastaet, a zatem pri ![]() rezko spadaet
[112].
rezko spadaet
[112].
<< 5. Standartnye modeli diskovyh | Oglavlenie | 5.2 Vertikal'naya struktura diskov >>
|
Publikacii s klyuchevymi slovami:
Fotometricheskaya sistema - slabye galaktiki - Skoplenie galaktik - fotometriya
Publikacii so slovami: Fotometricheskaya sistema - slabye galaktiki - Skoplenie galaktik - fotometriya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
![\begin{displaymath}
I(r) \approx I_0 \sqrt{\pi r/2h}\,e^{-r/h}\,\left[1+\frac{3}{8r/h}\right].
\end{displaymath}](http://images.astronet.ru/pubd/2006/08/23/0001215351/img445.gif)