<< 9.1 Poleznye formuly | Oglavlenie | 9.3 Rezul'taty izucheniya ... >>
9.2 Problemy issledovaniya dalekih galaktik
K sozhaleniyu, sushestvuyut po krainei mere tri
principial'nyh faktora, sil'no zatrudnyayushih nablyudatel'noe
issledovanie dalekih galaktik. Pervye dva svyazany s rasshireniem
Vselennoi, a tretii -- s evolyuciei ih harakteristik so vremenem.
![]() Oslablenie yarkosti
Oslablenie yarkosti
Pervaya iz pomeh -- eto tak nazyvaemoe
kosmologicheskoe oslablenie poverhnostnoi yarkosti, zavisyashee v modeli
rasshiryayusheisya Vselennoi tol'ko ot krasnogo smesheniya:
Kak vidno iz (98), rasshirenie Vselennoi privodit k
obeskurazhivayushe bystromu padeniyu poverhnostnoi yarkosti s rostom ![]() .
Ob'ekty s
.
Ob'ekty s ![]() imeyut v 3
imeyut v 3![]() raz men'shie yarkosti
(ili, v zvezdnyh velichinah,
raz men'shie yarkosti
(ili, v zvezdnyh velichinah, ![]() ) po sravneniyu s
analogichnymi ob'ektami vblizi nas. Galaktiki s
) po sravneniyu s
analogichnymi ob'ektami vblizi nas. Galaktiki s ![]() oslabevayut
na 7 zvezdnyh velichin (!). Sledovatel'no, dazhe s pomosh'yu kosmicheskih
nablyudenii sredi dalekih galaktik nam dostupny lish' te, kotorye imeyut
ochen' vysokuyu poverhnostnuyu yarkost' (naprimer, za schet moshnoi
vspyshki zvezdoobrazovaniya).
oslabevayut
na 7 zvezdnyh velichin (!). Sledovatel'no, dazhe s pomosh'yu kosmicheskih
nablyudenii sredi dalekih galaktik nam dostupny lish' te, kotorye imeyut
ochen' vysokuyu poverhnostnuyu yarkost' (naprimer, za schet moshnoi
vspyshki zvezdoobrazovaniya).
Padenie yarkosti s uvelicheniem ![]() (naryadu s vliyaniem
(naryadu s vliyaniem ![]() -popravki --
sm. dalee) privodit k eshe odnoi nablyudatel'noi
probleme -- pri sravnenii lineinyh razmerov galaktik, nablyudaemyh na raznyh
rasstoyaniyah, nel'zya ispol'zovat' ih izofotnye diametry (to est',
diametry, izmerennye v predelah fiksirovannogo znacheniya poverhnostnoi
yarkosti). Dlya eksponencial'nogo diska (43) pri
-popravki --
sm. dalee) privodit k eshe odnoi nablyudatel'noi
probleme -- pri sravnenii lineinyh razmerov galaktik, nablyudaemyh na raznyh
rasstoyaniyah, nel'zya ispol'zovat' ih izofotnye diametry (to est',
diametry, izmerennye v predelah fiksirovannogo znacheniya poverhnostnoi
yarkosti). Dlya eksponencial'nogo diska (43) pri ![]() radius v predelah izofoty
radius v predelah izofoty ![]() raven
raven
![]() (pri
(pri ![]() i
i
![]()
![]() ). Radius diska, nablyudaemogo na krasnom
smeshenii
). Radius diska, nablyudaemogo na krasnom
smeshenii ![]() , s ispol'zovaniem (98) mozhet byt' predstavlen kak
, s ispol'zovaniem (98) mozhet byt' predstavlen kak
![]() . Sledovatel'no, uzhe pri
. Sledovatel'no, uzhe pri ![]() izofotnyi radius diska umen'shaetsya na 0.38
izofotnyi radius diska umen'shaetsya na 0.38![]() ili primerno na 10%
opticheskogo radiusa. Pri
ili primerno na 10%
opticheskogo radiusa. Pri ![]() nablyudaemoe izmenenie radiusa
dostigaet 2.8
nablyudaemoe izmenenie radiusa
dostigaet 2.8![]() .
.
Dlya galaktiki, raspredelenie yarkosti kotoroi
opisyvaetsya zakonom Vokulera (11), izmenenie izofotnogo
radiusa s ![]() daetsya sleduyushei formuloi:
daetsya sleduyushei formuloi:
![]() ,
gde
,
gde
![]() . Dlya
ellipticheskoi galaktiki NGC 3379 s
. Dlya
ellipticheskoi galaktiki NGC 3379 s
![]() (sm. ris. 11)
izofotnyi radius pri
(sm. ris. 11)
izofotnyi radius pri
![]() raven
raven
![]() .
Pri
.
Pri ![]() radius galaktiki umen'shaetsya do 2.70
radius galaktiki umen'shaetsya do 2.70![]() (na 14%),
a pri
(na 14%),
a pri ![]() -- do 0.89
-- do 0.89![]() .
.
Pri sravnenii razmerov galaktik mozhno primenyat', naprimer,
velichiny ![]() (dlya eksponencial'nogo raspredeleniya) ili ispol'zovat'
podhod, osnovannyi na tak nazyvaemoi ''funkcii Petrosyana''
[252]. Eta funkciya (tochnee, velichina ei obratnaya) ravna
(dlya eksponencial'nogo raspredeleniya) ili ispol'zovat'
podhod, osnovannyi na tak nazyvaemoi ''funkcii Petrosyana''
[252]. Eta funkciya (tochnee, velichina ei obratnaya) ravna
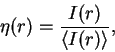 |
(99) |
Vtoroi zatrudnyayushii issledovaniya faktor sostoit v tom, chto pri
nablyudenii dvizhushegosya istochnika my registriruem v dannom intervale
dlin voln izluchenie, ispushennoe galaktikoi v drugom -- smeshennom --
diapazone. Ispravlenie nablyudenii za etot effekt nazyvaetsya
![]() -popravkoi.
Velichina
-popravkoi.
Velichina ![]() -popravki v zvezdnyh velichinah ravna
-popravki v zvezdnyh velichinah ravna
V chastnom sluchae, kogda raspredelenie energii v spektre
istochnika mozhet byt' opisano stepennym zakonom
![]() ,
formula (100) preobrazuetsya v prostoe analiticheskoe
vyrazhenie (sm., naprimer, [254]):
,
formula (100) preobrazuetsya v prostoe analiticheskoe
vyrazhenie (sm., naprimer, [254]):
.
U galaktik s bol'shimi krasnymi smesheniyami my nablyudaem v opticheskom
i IK diapazonah izluchenie, ispushennoe v korotkovolnovoi oblasti spektra.
Naprimer, izluchenie s
![]() Å ot galaktiki s
Å ot galaktiki s ![]() budet nablyudat'sya pri
budet nablyudat'sya pri ![]() v polose
v polose ![]() . Esli eta galaktika udalena
na
. Esli eta galaktika udalena
na ![]() , to ee UF izluchenie budet fiksirovat'sya v fil'tre
, to ee UF izluchenie budet fiksirovat'sya v fil'tre ![]() .
Osnovnaya problema pri uchete
.
Osnovnaya problema pri uchete ![]() -popravki sostoit v tom, chto raspredelenie
energii v korotkovolnovoi oblasti spektrov galaktik izvestno ploho
i poetomu znachenie etoi popravki dlya dalekih galaktik mozhet byt'
ochen' netochnym. Krome togo, na nablyudaemoe izluchenie galaktik v
UF diapazone sil'no vliyaet dazhe nebol'shoe kolichestvo pyli. Ob'ekty,
opticheski tonkie v vidimom diapazone, mogut byt' opticheski tolstymi
v UF.
-popravki sostoit v tom, chto raspredelenie
energii v korotkovolnovoi oblasti spektrov galaktik izvestno ploho
i poetomu znachenie etoi popravki dlya dalekih galaktik mozhet byt'
ochen' netochnym. Krome togo, na nablyudaemoe izluchenie galaktik v
UF diapazone sil'no vliyaet dazhe nebol'shoe kolichestvo pyli. Ob'ekty,
opticheski tonkie v vidimom diapazone, mogut byt' opticheski tolstymi
v UF.
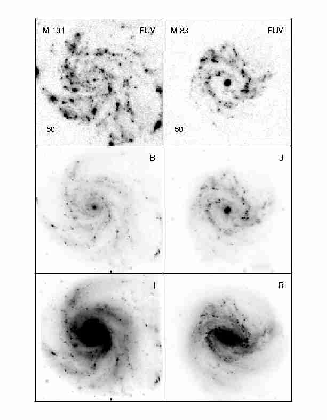 |
Bol'shaya rol' otnositel'nogo sdviga polos izlucheniya i
priema pri issledovanii dalekih ob'ektov illyustriruetsya
na ris. 50, gde dlya dvuh blizkih spiral'nyh galaktik sravnivayutsya izobrazheniya,
poluchennye v dalekoi ul'trafioletovoi oblasti spektra i v opticheskom
diapazone. Naglyadno vidno, chto morfologiya i raspredelenie poverhnostnoi
yarkosti ochen' sil'no menyayutsya pri smeshenii v UF diapazon.
V [256] bylo vypolneno modelirovanie togo, kak budut
vyglyadet' blizkie galaktiki, esli ih otnesti na raznye ![]() , i pokazano,
chto pri opticheskih fotometricheskih nablyudeniyah ob'ektov s
, i pokazano,
chto pri opticheskih fotometricheskih nablyudeniyah ob'ektov s ![]() prakticheski nevozmozhno poluchit' informaciyu ob ih istinnyh global'nyh
harakteristikah. Dlya kompensacii etogo effekta neobhodimo provodit'
nablyudeniya v bolee dlinnovolnovoi oblasti spektra.
prakticheski nevozmozhno poluchit' informaciyu ob ih istinnyh global'nyh
harakteristikah. Dlya kompensacii etogo effekta neobhodimo provodit'
nablyudeniya v bolee dlinnovolnovoi oblasti spektra.
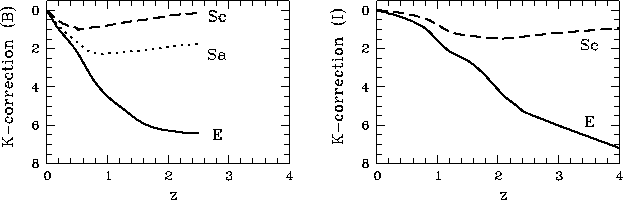 |
![]() -popravki dlya galaktik raznyh morfologicheskih tipov
v fil'trah
-popravki dlya galaktik raznyh morfologicheskih tipov
v fil'trah ![]() i
i ![]() soglasno [257]
pokazany na ris. 51 i privedeny v Prilozhenii (sm. takzhe [258]).
Na risunke vidno, chto otnositel'nyi sdvig polos izlucheniya i
priema privodit k sil'nomu zanizheniyu real'noi svetimosti vnegalakticheskogo
ob'ekta.
Sleduet takzhe obratit' vnimanie na nemonotonnost' znachenii popravok dlya
spiralei i ih bystryi rost s izmeneniem
soglasno [257]
pokazany na ris. 51 i privedeny v Prilozhenii (sm. takzhe [258]).
Na risunke vidno, chto otnositel'nyi sdvig polos izlucheniya i
priema privodit k sil'nomu zanizheniyu real'noi svetimosti vnegalakticheskogo
ob'ekta.
Sleduet takzhe obratit' vnimanie na nemonotonnost' znachenii popravok dlya
spiralei i ih bystryi rost s izmeneniem ![]() dlya
ellipticheskih galaktik. Raznoe povedenie
dlya
ellipticheskih galaktik. Raznoe povedenie ![]() dlya ob'ektov
raznyh tipov otrazhaet znachitel'nye otlichiya v raspredeleniyah energii
v ih spektrah.
dlya ob'ektov
raznyh tipov otrazhaet znachitel'nye otlichiya v raspredeleniyah energii
v ih spektrah.
![]() Popravka za evolyuciyu
Popravka za evolyuciyu
Pri interpretacii rezul'tatov fotometricheskogo izucheniya dalekih
galaktik i sravnenii ih s harakteristikami blizkih ob'ektov neobhodimo
uchityvat', chto dalekie ob'ekty mogut nahoditsya na bolee rannei stadii
svoei evolyucii. Fotometricheskaya struktura galaktik mozhet evolyucionirovat'
kak za schet zvezdno-dinamicheskih processov (naprimer, [101]),
tak i za schet evolyucii harakteristik sostavlyayushih ih zvezd.
Ellipticheskie galaktiki
Pri sil'no uproshennom podhode ellipticheskuyu galaktiku mozhno rassmatrivat' kak sovokupnost' zvezd, rodivshihsya odnovremenno v hode odinochnoi vspyshki zvezdoobrazovaniya. Prinyav etu gipotezu, my mozhem rasschitat' svetimost' i pokazateli cveta galaktiki na lyuboi moment vremeni (sm. Prilozhenie). Privedem, sleduya v osnovnom Tinsli [211], prostuyu analiticheskuyu model' evolyucii fotometricheskih svoistv ellipticheskoi galaktiki.
Predpolozhim, chto galaktika voznikla v moment vremeni ![]() v hode korotkoi odinochnoi vspyshki zvezdoobrazovaniya. Polnaya massa
vseh zvezd ravna M
v hode korotkoi odinochnoi vspyshki zvezdoobrazovaniya. Polnaya massa
vseh zvezd ravna M![]() , ih himicheskii sostav blizok k solnechnomu.
Nachal'naya funkciya mass (NFM) rodivshihsya zvezd opisyvaetsya stepennym zakonom
, ih himicheskii sostav blizok k solnechnomu.
Nachal'naya funkciya mass (NFM) rodivshihsya zvezd opisyvaetsya stepennym zakonom
![]() , gde
, gde ![]() -- massa zvezd vblizi
tochki povorota s glavnoi posledovatel'nosti (GP) v moment vremeni
-- massa zvezd vblizi
tochki povorota s glavnoi posledovatel'nosti (GP) v moment vremeni ![]() .
Vremya zhizni zvezd na GP (
.
Vremya zhizni zvezd na GP (![]() ) svyazano s ih massoi vyrazheniem
) svyazano s ih massoi vyrazheniem
![]() (
(
![]() ).
Svetimost' mozhet byt' vyrazhena cherez sootnoshenie massa-svetimost':
).
Svetimost' mozhet byt' vyrazhena cherez sootnoshenie massa-svetimost':
![]() , gde
, gde
![]() .
Polnaya svetimost' galaktiki v pervom priblizhenii mozhet byt' predstavlena
kak summa svetimostei zvezd, nahodyashihsya na GP, (karlikov) i gigantov:
.
Polnaya svetimost' galaktiki v pervom priblizhenii mozhet byt' predstavlena
kak summa svetimostei zvezd, nahodyashihsya na GP, (karlikov) i gigantov:
![]() .
.
Cherez vremya ![]() posle vspyshki zvezdoobrazovaniya na GP ostayutsya tol'ko
zvezdy v intervale mass ot
posle vspyshki zvezdoobrazovaniya na GP ostayutsya tol'ko
zvezdy v intervale mass ot ![]() (nizhnyaya granica NFM) do
(nizhnyaya granica NFM) do ![]() (massa
tochki povorota). Chislo takih zvezd v intervale mass
(massa
tochki povorota). Chislo takih zvezd v intervale mass
![]() ravno
ravno
Ispol'zuya (101) i (102) i vvedennye ranee approksimacii,
mozhno naiti integral'nye massy i svetimosti gigantov i zvezd na GP.
Tak, naprimer, otnoshenie polnoi massy gigantov k masse karlikov
so vremenem uvelichivaetsya, no ne prevyshaet velichiny ![]() .
Sledovatel'no, vklad gigantov v polnuyu zvezdnuyu massu galaktiki
prenebrezhim.
.
Sledovatel'no, vklad gigantov v polnuyu zvezdnuyu massu galaktiki
prenebrezhim.
Polnaya svetimost' zvezd na GP pri ![]() sostavlyaet
sostavlyaet
Otnoshenie svetimostei gigantov i zvezd na GP mozhet byt' predstavleno v sleduyushem vide:
Podstaviv v (105) realisticheskie znacheniya parametrov, poluchaem, chto v korotkovolnovoi (goluboi) oblasti spektra
Ocenim temp evolyucii integral'noi svetimosti ellipticheskoi galaktiki.
Polnaya svetimost' mozhet byt' predstavlena kak
Vtoroe slagaemoe v pravoi chasti (107) gorazdo men'she pervogo (sm. [211]) i poetomu
Sledovatel'no, v pervom priblizhenii temp evolyucii svetimosti ellipticheskih galaktik (
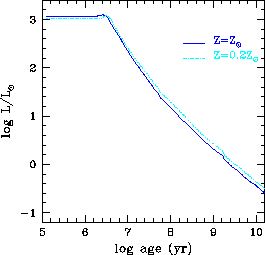
Provedennoe vyshe elementarnoe rassmotrenie priblizhenno soglasuetsya s
rezul'tatami detal'nyh chislennyh raschetov evolyucii fotometricheskih
harakteristik ellipticheskih galaktik [211]. Na ris. 52
dlya primera pokazano izmenenie so vremenem bolometricheskoi svetimosti
rodivshihsya v hode odinochnoi vspyshki zvezdoobrazovaniya zvezd dlya
dvuh znachenii metallichnosti. Pri ![]() let padenie svetimosti
v logarifmicheskih koordinatah proishodit pochti po lineinomu zakonu.
Za vremya ot
let padenie svetimosti
v logarifmicheskih koordinatah proishodit pochti po lineinomu zakonu.
Za vremya ot ![]() let posle vspyshki zvezdoobrazovaniya do
let posle vspyshki zvezdoobrazovaniya do ![]() let polnaya svetimost' umen'shaetsya bolee, chem na 4
let polnaya svetimost' umen'shaetsya bolee, chem na 4![]() .
.
 |
Pokazateli cveta zvezd, rodivshihsya v hode odinochnoi vspyshki
zvezdoobrazovaniya, so vremenem uvelichivayutsya (stanovyatsya krasnee).
Kak vidno iz privedennyh v Prilozhenii tablic, cveta real'nyh
ellipticheskih galaktik pri ![]() sootvetstvuyut pokazatelyam cveta zvezd
s vozrastom
sootvetstvuyut pokazatelyam cveta zvezd
s vozrastom ![]() let.
let.
Spiral'nye galaktiki
Spiral'nye galaktiki slozhnee ellipticheskih i ih nel'zya opisat' v vide odnorodnogo po vozrastu zvezdnogo naseleniya. Process zvezdoobrazovaniya v spiralyah prodolzhaetsya na protyazhenii vsei ih evolyucii i poetomu v lyuboi moment oni predstavlyayut soboi smes' zvezdnyh naselenii raznyh vozrastov. Pri analize fotometricheskoi evolyucii spiral'nyh galaktik v modeli neobhodimo zakladyvat' istoriyu zvezdoobrazovaniya (obychno rassmatrivaetsya postoyannaya skorost' zvezdoobrazovaniya ili zatuhayushaya so vremenem po eksponencial'nomu zakonu). V etom sluchae nel'zya ispol'zovat' prostye soobrazheniya, ispol'zovannye dlya analiza ellipticheskih galaktik, i takie ob'ekty mozhno izuchat' tol'ko na osnove chislennogo modelirovaniya [211].
Velichiny evolyucionnyh popravok dlya spiral'nyh galaktik, takzhe kak
i dlya ellipticheskih, mogut dostigat' neskol'kih zvezdnyh velichin
(naprimer, [257]) i, sledovatel'no, oni sravnimy s ![]() -popravkoi
i korrekciei za kosmologicheskoe oslablenie poverhnostnoi yarkosti
(pravda, evolyucionnaya popravka imeet drugoi znak -- dalekie, to est'
bolee molodye, ob'ekty yavlyayutsya bolee yarkimi).
-popravkoi
i korrekciei za kosmologicheskoe oslablenie poverhnostnoi yarkosti
(pravda, evolyucionnaya popravka imeet drugoi znak -- dalekie, to est'
bolee molodye, ob'ekty yavlyayutsya bolee yarkimi).
V zaklyuchenie etogo razdela sleduet upomyanut' eshe dva otnositel'no
slabo izuchennyh faktora, zatrudnyayushih interpretaciyu nablyudenii
dalekih ob'ektov. Pervyi faktor -- eto pogloshenie v mezhgalakticheskoi
srede. Vtoroi -- oslablenie izlucheniya za schet poglosheniya v diskah
proektiruyushihsya na luch zreniya galaktik. Pogloshenie v diskah fonovyh
galaktik ne yavlyaetsya ser'eznoi problemoi pri nablyudeniyah blizkih
ob'ektov. Soglasno privedennym v [260] raschetam, za schet
etogo effekta v polose ![]() teryaetsya ne bolee 5% izlucheniya ot
galaktiki, nahodyasheisya pri
teryaetsya ne bolee 5% izlucheniya ot
galaktiki, nahodyasheisya pri ![]() (eta ocenka zavisit ot prinyatoi
kosmologicheskoi modeli). Odnako dlya galaktiki na
(eta ocenka zavisit ot prinyatoi
kosmologicheskoi modeli). Odnako dlya galaktiki na ![]() eta dolya
uvelichivaetsya do
eta dolya
uvelichivaetsya do ![]() 30%.
30%.
<< 9.1 Poleznye formuly | Oglavlenie | 9.3 Rezul'taty izucheniya ... >>
|
Publikacii s klyuchevymi slovami:
Fotometricheskaya sistema - slabye galaktiki - Skoplenie galaktik - fotometriya
Publikacii so slovami: Fotometricheskaya sistema - slabye galaktiki - Skoplenie galaktik - fotometriya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
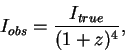
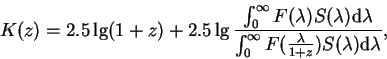
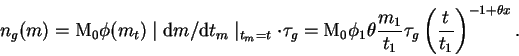
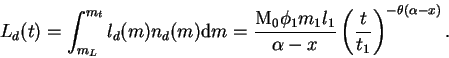
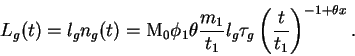
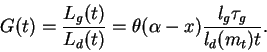
![\begin{displaymath}
L(t) = [1 + G(t)] L_d(t) =
\frac{{\rm M}_0 \phi_1 m_1 l_1}{\...
...a - x} (1+G) \left(\frac{t}{t_1}\right)^{-\theta(\alpha - x)}.
\end{displaymath}](http://images.astronet.ru/pubd/2006/08/23/0001215351/img986.gif)