Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Fizika Diskov
... processov1 Sistema, sostoyashaya iz bol'shogo chisla vzaimodeistvuyushih chastic, obladaet kollektivnymi svoistvami, chto proyavlyaetsya v samosoglasovannom dvizhenii vseh chastic, imeyushem volnovoi harakter. Volny mogut obmenivat'sya energiei i impul'som. Takogo roda vzaimodeistviya nazyvayut kollektivnymi. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...22] 1.1 Nedostatok veshestva v central'nyh oblastyah zvezdnyh diskov po sravneniyu s zakonom (1.1.2) ("dyra" ili depressiya plotnosti) zalozhen, naprimer, v modelyah Galaktiki [23,24] i ryade drugih [22]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... diska1.2 Zdes' my govorim o srednei po vsem tipam zvezd velichine 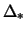. Otnositel'no haraktera raspredeleniya zvezd raznyh spektral'nyh klassov poperek ploskosti diska sm. v rabote Bartaya [26]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... bara1.3 Bar -- vytyanutoe ovalopodobnoe obrazovanie v centre nekotoryh (SB) galaktik ( sm. razd. 1.3). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... klassov1.4 Soglasno rabote [54], dispersiya skorostei zvezd prakticheski ne zavisit ot ih massy, no izmenyaetsya s ih vozrastom. Tak, dlya zvezd molozhe 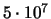let velichina 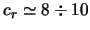km/s prakticheski ne otlichaetsya ot dispersii skorostei gazovyh oblakov, a dlya zvezd - karlikov, vozrast kotoryh blizok k vozrastu Galaktiki ( 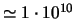let), 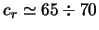km/s. 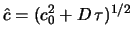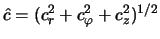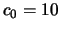Zavisimost' dispersii skorostei zvezd ot ih vozrasta udovletvoritel'no approksimiruetsya vyrazheniem , gde ; km/s; 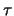-- vozrast zvezdy (v godah); 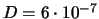(km/s)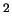/god. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... diska1.5 Na periferii ploskih galaktik za predelami ih spiral'nogo uzora sloi gaza chasto iskrivlyaetsya, otklonyayas' ot ploskosti simmetrii zvezdnogo diska na rasstoyanie do neskol'kih kiloparsek. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... diska1.6 Za isklyucheniem dalekih periferiinyh oblastei. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... galaktiku1.7 Takoi spiral'nyi uzor nazyvayut grand design. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... uzora1.8 Ih takzhe nazyvayut flukulentnymi spiralyami (flocculent). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... fona1.9 V nekotoryh redko vstrechayushihsya galaktikah rannih tipov s kraine nizkim soderzhaniem gaza vidny tol'ko slabokontrastnye spiral'nye vetvi po starym zvezdam [97]. V galaktikah s barom mozhet nablyudat'sya ves'ma moshnaya (do 50%) volna plotnosti v starom naselenii diska [91]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... galaktik1.10 V osnovnom u ellipticheskih galaktik, no est' i u neskol'kih spiral'nyh tipa Sa. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)1.11 V srednem u Sa-galaktik 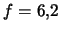, u Sb -- 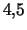, u Sc -- . 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
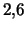... sistemah1.12 Pervym na eto obratil vnimanie Ya.B.Zel'dovich [130]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sistem1.13 Pri upotreblenii termina "tesnaya dvoinaya sistema" obychno podrazumevaetsya nalichie obmena mass mezhdu komponentami. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... nedel'1.14 V knige [118] priveden primer s RT Ser, u kotoroi umen'shenie na 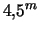proizoshlo za 27 let. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... II1.15 Vprochem, poka izvesten tol'ko odin "Bystryi barster" MXB 1730--335 s harakternym vremenem povtoreniya 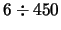s. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... izmenitsya2.1 Otnositel'no postroeniya kineticheskogo uravneniya v proizvol'noi ortogonal'noi sisteme koordinat sm. v monografii Polyachenko i Fridmana [1]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... gaza2.2 O roli gaza sm. gl. 4 i 6. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...epiciklicheskim2.3 Podrobnee sm. pp. 1.1.3, 2.2.2. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq2.1.34)2.4 Analiz vliyaniya vozmozhnogo otkloneniya funkcii raspredeleniya zvezd po ostatochnym skorostyam ot anizotropnogo maksvellovskogo na gravitacionnuyu ustoichivost' zvezdnogo diska proveden v p. 2.3.4. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... marginal'noi2.5 T.e. nahodyasheisya na granice ustoichivosti. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vide2.6 V ryade rabot v ramkah razlichnyh modelei gravitiruyushego diska bylo pokazano, chto VKB-priblizhenie daet rezul'taty, ves'ma blizkie k tochnym i dlya krupnomasshtabnyh mod. Tak, naprimer, po Kalnaisu [194], VKB-reshenie uravneniya Puassona dlya mody 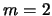, 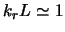otlichaetsya ot tochnogo ne bolee, chem na 2%, a v rabote [195] tochnye znacheniya chastot kolebanii diska prakticheski sovpadayut s vychislennymi v korotkovolnovom priblizhenii vplot' do samyh krupnomasshtabnyh mod vklyuchitel'no. Poetomu ispol'zovanie VKB-priblizheniya vpolne mozhet privodit' k rezul'tatam udovletvoritel'noi tochnosti vplot' do 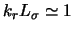. Eto, odnako, zavedomo ne otnositsya k okrestnostyam dinamicheskih rezonansov takih mod, gde 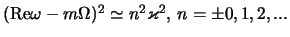-- sm. nizhe (2.2.22). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sootnosheniem2.7 Primes' "yam bol'shei glubiny", sootvetstvuyushih chetnym po 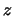-koordinate sobstvennym funkciyam 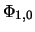, soglasno [192] umen'shaet velichinu v oblasti 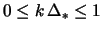ne bolee, chem na 2%. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vetvi2.8 Termin "gradientnaya" obuslovlen tem, chto v odnorodnom po 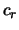i diske eta vetv' kolebanii vyrozhdaetsya ( ). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
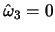... holodnyi2.9 "Temperatura" zvezdnoi sistemy harakterizuetsya kvadratami dispersii skorostei zvezd (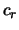, ,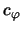), a gaza -- skorosti zvuka .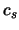 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sloi2.10 Stpogo govopya v etom sluchae sistema nestacionapna. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
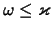... 2.11 V besstolknovitel'nom diske imeyutsya i vysokochastotnye kolebaniya s 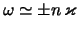, 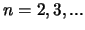[sm.(2.2.38)]. Po krainei mere v odnorodnom diske oni ne vliyayut na gravitacionnuyu ustoichivost'. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...2.12 Analogichnyi rezul'tat poluchen v rabote [208]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sushestvennoi2.13 K sozhaleniyu, eti trudnosti nosyat principial'nyi harakter. Vyhodom iz etogo polozheniya mozhet sluzhit' sravnenie s kontrol'nymi chislennymi eksperimentami (sm. gl. 3), v kotoryh neodnorodnye sistemy vyhodyat na granicu ustoichivosti, i pri neobhodimosti korrektirovka kriteriev ustoichivosti takogo tipa. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... shlangovaya2.14 Termin, obychno upotreblyaemyi v fizike plazmy i gidrodinamike. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... znachenii3.1 V modelyah PP pri "izmerenii" makroskopicheskih (v tom chisle i lokal'nyh) parametrov diska, prihodyashego v sostoyanie, blizkoe k stacionarnomu, ispol'zuyut usrednenie po promezhutkam vremeni poryadka neskol'kih desyatkov vremennyh shagov ( ). Eto effektivno uvelichivaet chislo uchastvuyushih v eksperimente chastic v 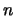raz. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... zvezd3.2 Rasseyannye zvezdnye i sharovye skopleniya soderzhat sootvetstvenno 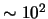i zvezd i metod PP naibolee aktivno ispol'zuetsya dlya modelirovaniya etih sistem. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... preimushestv3.3 Prezhde vsego sily opredelyayutsya s takoi zhe tochnost'yu, chto i arifmeticheskaya tochnost' EVM. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... chastotu3.4 Poskol'ku v opredelenie 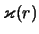vhodit proizvodnaya 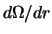, velichinu 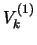neobhodimo predvaritel'no sgladit', vychislit' 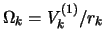, a zatem i . 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...218]3.5 Cel' etih eksperimentov zaklyuchalas', v chastnosti, v proverke usloviya ustoichivosti diska (2.4.21). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
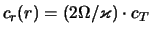... 3.6 Disk, nahodyashiisya na granice ustoichivosti otnositel'no melkomasshtabnyh vozmushenii ( 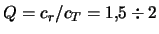, imeet 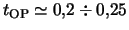, chto, kak vidim, nedostatochno dlya stabilizacii global'noi bar-mody. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... zvezd3.7 Otmetim, chto v ramkah obsuzhdaemyh eksperimentov rassmatrivalas' osobennost' v raspredelenii GMO -- kol'co povyshennoi plotnosti v oblasti 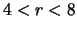(kpk) [72]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... bar-moda3.8 V samyh vnutrennih oblastyah nekotoryh galaktik nablyudayutsya gazovye (molekulyarnye) bary. Bol'shaya poluos' etih struktur sostavlyaet pk, chto sushestvenno men'she po sravneniyu s tipichnymi zvezdnymi barami [301,302]. Prichem molekulyarnye yadernye bary nablyudayutsya kak v sistemah so zvezdnym barom, tak i v galaktikah bez bara. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... gaza4.1 Obobshenie na sluchai davleniya izlucheniya sm. [463], pazd.5.3. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vid4.2 Obsuzhdenie modeli tonkogo diska i ee obobshenie mozhno naiti v monogpafii Gop'kavogo i Fpidmana [185]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
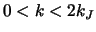...4.3 V deistvitel'nosti etot interval mozhet byt' neskol'ko uzhe, poskol'ku pri 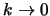narushaetsya VKB-priblizhenie. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... chlenov4.4 Esli v dvumepnoi modeli fopmal'no polozhit' 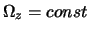, to ona budet opisyvat' tpehmepnuyu dinamiku chastnogo klassa vozmushenii, ne imeyushih popepechnoi k ploskosti diska komponenty volnovogo vektopa. Ppi etom pod 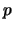, , 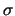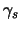sleduet podpazumevat' ne povephnostnye, a ob'emnye davlenie, plotnost', pokazatel' adiabaty. Ha eto ukazal V.V. Muscevoi. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... neobychnym4.5 V analogichnoi po postanovke ploskoi zadache vozmushennoe davlenie 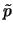yavlyaetsya nepreryvnym pri perehode cherez poverhnost' razryva skorosti [327]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq4.5.18)]4.6 Takaya zavisimost' proyavlyaetsya v sleduyushem za (4.5.22) poryadke: . 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
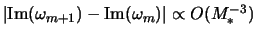... galaktik4.7 Gipoteza ob otvetstvennosti gidrodinamicheskih neustoichivostei v gazovom diske za vozbuzhdenie spiral'nogo uzora galaktik byla sformulirovana A.M.Fridmanom v 1972 g. Konkretnye soobrazheniya o gidrodinamicheskom mehanizme vozbuzhdeniya spiralei i meste ego lokalizacii v galaktikah byli vyskazany v rabote [50]. Pozdnee byli izucheny gidrodinamicheskie neustoichivosti v trehmernyh modelyah gravitiruyushei sredy [345-348] i gazovom diske [351,353]. Provedennoe zatem eksperimental'noe issledovanie centrobezhnoi neustoichivosti na ustanovkah s vrashayusheisya "melkoi vodoi" [354,355] pozvolilo v konechnom schete sformulirovat' gidrodinamicheskuyu koncepciyu proishozhdeniya spiral'nogo uzora ploskih galaktik (sm. gl. 6). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... zametnym4.8 Tak, dlya dvuhrukavnyh vozmushenii pri 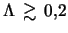velichina 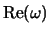men'she poluchaemoi iz (4.5.21) na 3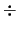0 40%. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Galaktike4.9 Zametim takzhe, chto plotnoe kol'co gaza voznikaet v chislennyh gazodinamicheskih modelyah s barom [326] i v vyazkih osesimmetrichnyh modelyah diska [360]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...)4.10 V rabotah [362,363] obsuzhdayutsya vozmozhnye metodiki i trudnosti nablyudatel'nogo opredeleniya parametra . 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
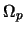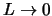... 4.11 Etot faktor i zatrudnyaet nahozhdenie nizkochastotnoi mody, poskol'ku v razryvnoi modeli etoi neustoichivosti net. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
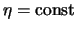... 4.12 Takoi podhod analogichen rassmotrennomu v razd. 5.2. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... volny4.13 V rabote Kovalenko i Levi [394] v ramkah analiticheskogo podhoda rassmotreno sverhzvukovoe techenie cherez potencial'nuyu yamu s ustanovleniem stacionarnoi pri opredelennyh usloviyah (vid potenciala i parametry techeniya) udarnoi volny v oblasti vtekaniya gaza v yamu. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... t.p.5.1 Pri takom podhode vpolne umestna analogiya s padayushim orbital'nym sputnikom, popavshim v verhnie sloi atmosfery Zemli. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vide5.2 V literature ochen' chasto ispol'zuyutsya vyrazheniya tipa (5.1.6), (5.1.9), (5.1.15), 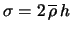i t.p., razlichayushiesya koefficientami poryadka edinicy, chto svyazano s razlichiem v usrednenii po 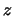-koordinate. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... AD5.3 Vpervye takogo roda resheniya byli polucheny v rabote [415]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... knigi5.4 Izmenenie tempa istecheniya veshestva iz opticheskogo komponenta v TDS mozhet byt' vyzvano dinamicheskimi neustoichivostyami v zvezde [131,414,418-420]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... energii5.5 V stacionarnoi modeli polnaya svetimost' diska opredelyaetsya polovinoi gravitacionnoi energii padayushego veshestva. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...5.6 Liang [430] postroil svoi modeli v cilindricheskoi sisteme koordinat .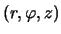 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vyazkost'yu5.7 Rech' idet o fizicheskoi vyazkosti, no obychno ispol'zuemye chislennye shemy obladayut takzhe chislennoi vyazkost'yu. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... volnami5.8 Sm. podrobnee p. 5.2.3. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... adiabaty5.9 V svyazi s vyborom velichiny pokazatelya adiabaty sleduet pomnit', chto znacheniyu v trehmernom sluchae sootvetstvuet 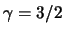v dvumernyh modelyah (p. 4.1.1). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... uravneniyu5.10 Nebol'shie razlichiya v chislovyh koefficientah u raznyh avtorov svyazany so sposobom usredneniya po 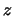-koordinate ishodnyh uravnenii. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... gazovomu5.11 Takuyu vyazkost' nazyvayut magnitnoi. Eto svyazano s tem, chto turbulentnoe dinamo generiruet magnitnoe pole 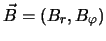, prichem 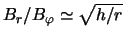i magnitnoe davlenie sravnimo s gazovym. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig5.16)5.12 Zdes' my polagaem, chto disk pokoitsya, a dvizhutsya naruzhnye oblasti. Obratnyi perehod proizvoditsya obychnym doplerovskim preobrazovaniem chastoty. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... vektoru5.13 Drugimi slovami, vdol' poverhnosti razryva gaz ubegaet ot volny bystree, chem ona ego dogonyaet. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...5.14 Sluchai 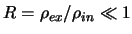naibolee interesen v prilozhenii k diskovoi akkrecii na zamagnichennye kompaktnye ob'ekty, gde sushestvuet problema proniknoveniya veshestva v magnitosferu i plotnost' ego tam sushestvenno nizhe po sravneniyu s plotnost'yu diska. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... uravnenie5.15 V predele 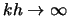eto uravnenie rassmotreno v rabote [473], a dlya -- v [150]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... Papaloizu-Pringla5.16 Dannyi punkt napisan sovmestno s V.V. Muscevym. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... diski5.17 Sm. p. 5.1.6. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... velichine5.18 Kak pokazyvaet chislennoe reshenie, plotnost' potoka uglovogo momenta vozmushenii vezde v diske napravlena naruzhu. Eto yavlyaetsya otrazheniem fundamental'nogo principa Le-Shatel'e -- neustoichivye spiral'nye mody otvodyat naruzhu uglovoi moment veshestva, akkreciruyushego i tem samym vysvobozhdayushego gravitacionnuyu energiyu. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... garmonik5.19 Superpoziciya neustoichivyh mod s bol'shim inkrementom, kak pravilo, nevozmozhna, poskol'ku naibolee bystro rastushaya moda na nelineinom etape "pereklyuchaet na sebya" energeticheskii istochnik neustoichivosti. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... tyazhesti5.20 V fizike plazmy ih nazyvayut diffuzionnymi, perestanovochnymi. Tyazhelaya zhidkost' nad legkoi, holodnaya nad goryachei, plazma nad magnitnym polem -- vse eto primery razvitiya dannogo tipa neustoichivostei. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sisteme5.21 Dannyi rezonans horosho izvesten v nebesnoi mehanike v ogranichennoi zadache treh tel. Primerami yavlyayutsya osobennosti dvizheniya asteroidov v sisteme Solnce-Yupiter i nekotopye osobennosti struktury kolec Saturna s uchetom sputnikov planety. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... sluchae6.1 Shirinu rezonansnoi oblasti my ne vychislyaem, poskol'ku, kak budet vidno iz privedennyh nizhe ocenok, maksimal'nyi inkrement issleduemoi neustoichivosti poryadka ili men'she obratnogo vremeni radial'nogo snosa paketa spiral'nyh gravitacionnyh voln [453]. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...496]6.2 Analogichnyi podhod pozvolil razvit' teoriyu dreifovogo dvizheniya zaryazhennyh chastic v magnitnom pole posredstvom usredneniya ih real'nogo dvizheniya po "bystroi" faze larmorova vrasheniya. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... gidrodinamicheskim)6.3 Shodnaya ideya vyskazyvalas' A.M.Fridmanom [503], ob'yasnyavshim mnogoyarusnost' spiral'noi struktury -- razlichnoe chislo rukavov v razlichnyh oblastyah diska po 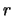-- tem, chto v etih oblastyah sushestvuyut razlichnye usloviya dlya predpochtitel'nogo razvitiya toi ili inoi neustoichivosti. Kazhdaya iz etih neustoichivostei harakterizuetsya svoei zavisimost'yu maksimal'nogo inkrementa ot nomera azimutal'noi mody 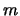, chto i privodit k razlichnym vidam spiral'noi struktury v raznyh oblastyah sistemy. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Publikacii s klyuchevymi slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [2]
Ocenka: 2.9 [golosov: 78]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya