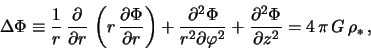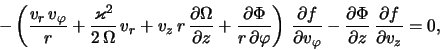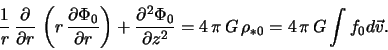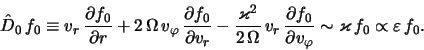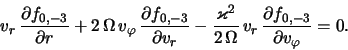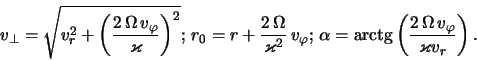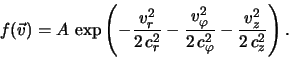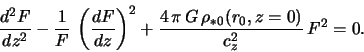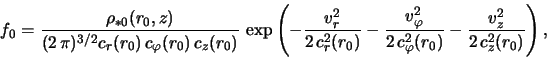---

<< 2. Dinamika zvezdnogo diska | Oglavlenie | 2.2 Dinamika vozmushenii ... >>

Razdely

• 2.1.1 Ishodnye uravneniya
• 2.1.2 Ravnovesnaya funkciya raspredeleniya zvezd

---

2.1 Ravnovesie

2.1.1 Ishodnye uravneniya

Harakternoe vremya, v techenie kotorogo parametry dvizheniya otdel'noi zvezdy mogut zametno izmenit'sya blagodarya parnomu gravitacionnomu vzaimodeistviyu s drugimi zvezdami v diskah ploskih galaktik, namnogo bol'she vremeni sushestvovaniya etih sistem [61]. Poetomu strukturu i dinamiku zvezdnyh diskov galaktik s horoshei tochnost'yu mozhno opisyvat' s pomosh'yu besstolknovitel'nogo kineticheskogo uravneniya. V dekartovyh koordinatah eto uravnenie imeet vid

gde -- funkciya raspredeleniya zvezd v shestimernom fazovom (koordinatno-skorostnom) prostranstve, -- gravitacionnyi potencial. Podcherknem, chto vektornuyu formu my ispol'zovali isklyuchitel'no dlya kratkosti zapisi, i pri perehode k drugoi sisteme koordinat vid uravneniya (2.1.1) izmenitsya^2.1.

Zvezdnye diski galaktik v znachitel'noi mere obladayut osevoi simmetriei, chto yavlyaetsya estestvennym sledstviem ih vrasheniya. Po etoi prichine dlya resheniya mnogih problem dinamiki zvezdnogo diska udobno pol'zovat'sya uravneniem (2.1.1), zapisannym v cilindricheskih koordinatah [1]:

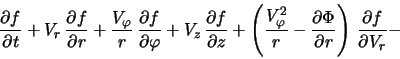
Uravnenie (2.1.2) moglo by polnost'yu opisyvat' dinamiku zvezdnogo diska, esli by byl zadan gravitacionnyi potencial . Velichina poslednego opredelyaetsya raspredeleniyami prostranstvennyh plotnostei vseh podsistem galaktiki -- v osnovnom zvezd diska , sferoidal'noi i ploskoi gazovoi . V ob'eme, zanyatom zvezdnym diskom, velichina mala po sravneniyu s , dazhe esli massa diska sravnima s massoi galo (sm. p. 1.3.2). Poetomu, interesuyas' dinamikoi zvezdnogo diska, mozhno v pervom priblizhenii potencial galo schitat' vneshnim, ne zavisyashim ot vremeni.

V osesimmetrichnyh zadachah ili sistemah bez gaza^2.2 gravitacionnyi potencial, opredelyayushii dinamiku zvezdnogo diska, prakticheski mozhno schitat' samosoglasovannym i tem samym svyazat' velichiny i cherez ob'emnuyu plotnost' zvezdnogo diska uravneniem Puassona

gde -- gravitacionnaya postoyannaya, a velichiny i svyazany ochevidnym sootnosheniem

Vyshe uzhe upominalas' otnositel'naya malost' amplitud neosesimmetrichnyh vozmushenii plotnosti zvezdnogo diska. Krome togo, esli otvlech'sya ot upomyanutyh osobennostei, raspredeleniya razlichnyh velichin v diskah prakticheski ne izmenyayutsya v techenie vremennyh promezhutkov poryadka neskol'kih oborotov diska. I tem samym funkciyu raspredeleniya zvezd diska mozhno predstavit' v vide summy stacionarnoi osesimmetrichnoi i "vozmushennoi" komponent.

Kak uzhe otmechalos' v obzore nablyudatel'nyh dannyh (sm. razd. 1.1), osnovnym dvizheniem zvezd v diske yavlyaetsya ih vrashenie vokrug osi simmetrii ploskoi galaktiki. V sootvetstvii s etim udobno vydelit' uglovuyu skorost' vrasheniya diska

i vvesti ostatochnuyu skorost' sootnosheniyami

Netrudno videt', chto takoe preobrazovanie privedet ishodnoe kineticheskoe uravnenie (2.1.2) k vidu

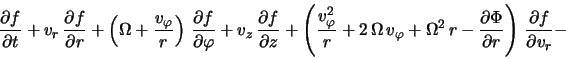
gde -- epiciklicheskaya chastota (chastota malyh kolebanii zvezd diska v radial'nom napravlenii -- sm.razd. 1.1).

2.1.2 Ravnovesnaya funkciya raspredeleniya zvezd

Ravnovesnaya (stacionarnaya i osesimmetrichnaya) komponenta funkcii raspredeleniya zvezd diska, soglasno (2.1.7), dolzhna udovletvoryat' uravneniyu

gde -- stacionarnaya osesimmetrichnaya chast' gravitacionnogo potenciala, opisyvaemaya uravneniem Puassona

Sistema uravnenii (2.1.8), (2.1.9) samosoglasovanna i v sootvetstvii s privedennymi vyshe zamechaniyami mozhet sluzhit' dlya opredeleniya funkcii i . Ona dovol'no slozhna, i dlya dal'neishego prodvizheniya v reshenii postavlennoi nami zadachi neobhodimo ispol'zovat' priblizheniya, osnovaniem dlya primeneniya kotoryh dolzhny byt' dannye nablyudenii.

Iz etih dannyh v pervuyu ochered' sleduet, chto harakternaya polutolshina zvezdnogo diska mnogo men'she ego radiusa . Eto oznachaet, chto v uravnenii (2.1.9) i v prosteishem priblizhenii odnorodnogo po tolshine diska iz (2.1.9) vytekaet ocenka chastoty kolebanii zvezd poperek ploskosti diska [sm. (1.1.4)]:

gde -- ravnovesnaya poverhnostnaya plotnost' zvezdnogo diska. Ochevidno, chto dlya zadannogo znacheniya velichina pri . V etom zhe predele chastota kolebanii zvezd v ploskosti diska ostaetsya konechnoi velichinoi [186]. Poetomu v teorii, izuchayushei strukturu dostatochno tonkih zvezdnyh diskov, poyavlyaetsya malyi parametr [sm. ocenku (1.1.6)]

Iz privedennyh vyshe rassuzhdenii sleduet, chto amplituda kolebanii zvezd poperek ploskosti diska est' velichina poryadka , a -komponenta ih skorosti . Poetomu v uravnenii (2.1.8) operatory i . S drugoi storony, ispol'zuya uravneniya dvizheniya otdel'noi zvezdy poperek ploskosti diska, vidim: . Poetomu svyazannaya s -dvizheniem zvezd chast' kineticheskogo uravneniya (2.1.8) imeet vid

Iz dannyh nablyudenii takzhe sleduet (sm. p. 1.1.1), chto harakternye dispersii komponent ostatochnyh skorostei zvezd [sm. (2.1.6)] maly po sravneniyu so skorost'yu vrasheniya zvezd diska vokrug centra mass galaktiki:

gde , . Malaya velichina etogo parametra oznachaet, chto ; i, sledovatel'no, chlenami i v uravnenii (2.1.8) mozhno prenebrech'. Priblizhenie, v kotorom ukazannymi chlenami prenebregayut, nazyvaetsya epiciklicheskim^2.3. Chlenom my prenebregat' ne budem, poskol'ku harakternye masshtaby radial'noi neodnorodnosti parametrov diska za predelami ego central'noi chasti maly po sravneniyu s rasstoyaniem do centra diska [8].

Priblizhenie, opredelyaemoe neravenstvom (2.1.13), daet osnovanie zaklyuchit', chto ravnovesie diska v radial'nom napravlenii obuslovleno balansom centrobezhnoi i ravnovesnoi gravitacionnoi sil

s tochnost'yu do chlenov .

Iz privedennoi vyshe ocenki sleduet, chto zavisyashaya ot chast' ravnovesnogo gravitacionnogo potenciala . Imenno eta velichina i opredelyaet poryadok po parametru zavisyashei ot -koordinaty komponenty uglovoi skorosti vrasheniya diska. Deistvitel'no, tak kak polnaya , gde , iz usloviya ravnovesiya diska (2.1.14) poluchim

i, sledovatel'no,

Za vychetom etogo vklada i [sm. (2.1.12)] ostavshayasya sovokupnost' chlenov v (2.1.8) est'

Poluchennye rezul'taty, ocenivayushie soglasno (2.1.12), (2.1.16), (2.1.17) poryadki chlenov kineticheskogo uravneniya po malomu parametru , pozvolyayut pereiti k resheniyu postavlennoi nami zadachi opredeleniya i metodom posledovatel'nyh priblizhenii. Dlya realizacii etoi vozmozhnosti zametim, chto iz elementarnoi ocenki sleduet i, sledovatel'no, . Poetomu razlozheniya iskomyh funkcii i v ryady po stepenyam parametra dolzhny imet' vid

gde ; . Razlozhenie po chetnym stepenyam obuslovleno tem, chto ego zavisimost' ot opredelyaetsya tol'ko parametrom tolshiny diska . Eto utverzhdenie spravedlivo i dlya , no neobyazatel'no dolzhno vypolnyat'sya dlya .

Podstavim razlozheniya (2.1.18),(2.1.19) v ishodnuyu sistemu uravnenii (2.1.8), (2.1.9). Togda v dvuh glavnyh poryadkah po parametru poluchim

gde

Esli by proekciya traektorii zvezdy na ploskost' predstavlyala soboi okruzhnost', to blagodarya stacionarnosti i osesimmetrichnosti ravnovesnogo sostoyaniya diska velichina

byla by integralom dvizheniya. Real'no zhe radial'naya koordinata zvezdy yavlyaetsya medlenno menyayushimsya (v svyazi s tem, chto ) parametrom. Poetomu priblizhenno sohranyayusheisya velichinoi dolzhen byt' adiabaticheskii invariant [52] i dlya resheniya privedennoi vyshe sistemy uravnenii udobno pereiti ot peremennyh k peremennym tipa deistvie-ugol [186]:

V etih peremennyh sistema (2.1.20), (2.1.21) primet vid

Otsyuda vidno, chto ne zavisit ot peremennoi . Poskol'ku opredelenie i yavlyaetsya nashei zadachei, prointegriruem (2.1.28) po polnomu periodu izmeneniya velichiny . V rezul'tate poluchim

Pereidem teper' k peremennym ,, , svyazannym s velichinami , , sootnosheniyami

Kak budet vidno iz soderzhaniya sleduyushego razdela, velichina imeet smysl amplitudy radial'noi skorosti zvezdy, predstavlyaet soboi radius krugovoi orbity centra epicikla zvezdy, a velichina yavlyaetsya fazoi dvizheniya zvezdy po epiciklu. Poskol'ku v ramkah ispol'zuemogo nami epiciklicheskogo priblizheniya , to v (2.1.30), (2.1.31) sleduet polagat' , .

Netrudno videt', chto v novyh peremennyh (2.1.31) uravnenie (2.1.29) priobretaet vid

S uchetom uravneniya (2.1.27) otsyuda sleduet iskomaya ravnovesnaya funkciya raspredeleniya zvezd

Eto oznachaet, chto v ramkah ispol'zuemyh nami priblizhenii (epiciklicheskogo i glavnogo poryadka po parametru ) velichiny , , yavlyayutsya integralami dvizheniya.

Konkretnyi vid etoi funkcii dolzhen byt' opredelen na osnovanii dopolnitel'nyh dannyh. Neposredstvenno postroit' funkciyu raspredeleniya , ishodya iz nablyudenii, v nastoyashee vremya predstavlyaetsya vozmozhnym tol'ko v solnechnoi okrestnosti Galaktiki. Neravenstvo dispersii skorostei zvezd Galaktiki v treh vzaimno perpendikulyarnyh napravleniyah yavlyaetsya neprelozhnym nablyudatel'nym faktom (sm. p. 1.1.4). Imeetsya ryad analiticheskih approksimacii nablyudaemyh raspredelenii skorostei zvezd, kotorye soglasuyutsya s nablyudeniyami tol'ko v ogranichennyh intervalah skorostei (obzor literatury dan Shacovoi [187]). Naibolee izvestno raspredelenie Shvarcshil'da, kotoroe predstavlyaet soboi anizotropnoe maksvellovskoe:

Byli predprinyaty bol'shie usiliya dlya togo, chtoby, s odnoi storony, obosnovat' etot zakon teoreticheski [188,189], a s drugoi -- ustranit' protivorechiya s nablyudeniyami putem uvelicheniya chisla i tochnosti nablyudenii. V itoge mozhno skazat', chto lish' dlya malyh i srednih skorostei zvezd udaetsya poluchit' udovletvoritel'noe soglasie zakona (2.1.34) s nablyudeniyami. Dlya oblasti bol'shih skorostei rashozhdeniya sushestvenny [187]. Odnako, nesmotrya na nalichie opredelennyh trudnostei prezhde vsego teoreticheskogo plana, zakon Shvarcshil'da yavlyaetsya naibolee populyarnym v zvezdnoi astronomii. Nizhe nami budet ispol'zovat'sya raspredelenie v forme (2.1.34)^2.4. V sootvetstvii s etim polagaem

gde , parametry , imeyut ochevidnyi smysl dispersii skorostei zvezd v radial'nom i perpendikulyarnom k ploskosti diska napravleniyah sootvetstvenno, a iz (2.1.31) netrudno videt', chto rol' dispersii skorostei zvezd v azimutal'nom napravlenii igraet velichina

Eto sootnoshenie mezhdu i s horoshei tochnost'yu sootvetstvuet imeyushimsya dannym astronomicheskih nablyudenii [56,57].

Vychislim ravnovesnoe raspredelenie ob'emnoi plotnosti v diske. Dlya etogo prointegriruem (2.1.35) po prostranstvu skorostei

gde

-- razmernaya konstanta [sm. (2.1.35)]. Polozhim teper', chto

Togda uravnenie Puassona (2.1.22) v glavnom poryadke po malomu parametru perehodit v uravnenie, opredelyayushee funkciyu :

Netrudno videt', chto ubyvayushee pri reshenie etogo uravneniya imeet vid

gde parametr

imeet ochevidnyi smysl harakternoi polutolshiny zvezdnogo diska, a velichina

predstavlyaet soboi ravnovesnuyu poverhnostnuyu plotnost' zvezdnogo diska.

Summiruem poluchennye rezul'taty. Ravnovesnaya funkciya raspredeleniya zvezd v glavnom poryadke po malomu parametru i v epiciklicheskom priblizhenii, opredelyaemom neravenstvom (2.1.13), imeet vid

gde

a raspredelenie ravnovesnogo gravitacionnogo potenciala poperek ploskosti diska opisyvaetsya sootnosheniem

Kak vidno iz (2.1.44)-(2.1.46), ravnovesie diska opredelyaetsya raspredeleniyami sleduyushih parametrov: , , , , , , . Odnako ne vse iz nih nezavisimy. Tak, velichina odnoznachno opredelyaetsya cherez uglovuyu skorost' sootnosheniem (1.1.5), a parametry , , a takzhe , , svyazany uravneniyami (2.1.36) i (2.1.42) sootvetstvenno. Eshe odnu svyaz' mezhdu ravnovesnymi parametrami zvezdnogo diska moglo by dat' uravnenie (2.1.14), esli by massa diska v ploskih galaktikah vsegda byla mnogo bol'she massy sferoidal'nyh podsistem. V etom sluchae my mogli by svyazat' [a cherez uravnenie Puassona i ] s uglovoi skorost'yu vrasheniya diska . K sozhaleniyu, upomyanutoe uslovie ne vypolnyaetsya, i poetomu v ramkah razvitoi vyshe teorii imeyutsya chetyre nezavisimyh parametra, opisyvayushih zvezdnyi disk. Kak budet vidno iz dal'neishego, eshe dve svyazi mezhdu ravnovesnymi parametrami zvezdnogo diska mozhno v principe poluchit' iz uslovii ego marginal'noi^2.5 ustoichivosti otnositel'no izgibnyh vozmushenii i vozmushenii v ego ploskosti. Togda nezavisimymi i, sledovatel'no, trebuyushimi opredeleniya iz dannyh nablyudenii ostanutsya lish' dva parametra. Odnim iz nih obychno polagayut uverenno nablyudaemuyu uglovuyu skorost' vrasheniya diska . Drugim mozhet byt' libo odna iz dispersii skorostei zvezd ( ) v diske, libo ego poverhnostnaya plotnost' . Velichina poslednei iz nablyudenii uverenno ne opredelyaetsya, odnako iz dannyh po mnogocvetnoi fotometrii zvezdnyh diskov izvestno, chto za predelami central'noi ( ) chasti diska [8,10].

V etom razdele my, sleduya Vandervoortu [186], postroili dovol'no prostuyu model' zvezdnogo diska. Bolee slozhnye modeli struktury diska poperek ego ploskosti mozhno naiti, naprimer, v upominavsheisya uzhe rabote Vandervoorta i rabote Bakola [190]. V poslednei, v chastnosti, uchten vklad ob'emnoi plotnosti zvezd sferoidal'noi podsistemy (sm. takzhe rabotu [191]). My ih, odnako, opisyvat' ne budem. Vo-pervyh, potomu, chto dovol'no tonkie detali modelei ves'ma trudno sravnivat' s dannymi nablyudenii. Vo-vtoryh, potomu, chto zadacha postroeniya teorii ustoichivosti etih modelei zvezdnyh diskov otnositel'no kak izgibnyh vozmushenii, tak i vozmushenii v ih ploskosti poka ne reshena, i tem samym celostnogo ponimaniya dinamiki zvezdnogo diska v ramkah takih modelei ne voznikaet.

---

<< 2. Dinamika zvezdnogo diska | Oglavlenie | 2.2 Dinamika vozmushenii ... >>

Publikacii s klyuchevymi slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Sm. takzhe: Iskrivlennyi disk NGC 4753 Akkrecionnyi disk chernoi dyry: vizualizaciya Dvazhdy iskrivlennyi mir dvoinyh chernyh dyr Spiral'nyi disk vokrug chernoi dyry V centre spiral'noi galaktiki NGC 3521 Massivnaya chernaya dyra razryvaet proletayushuyu zvezdu Ul'trafioletovye kol'ca M31 Vse publikacii na tu zhe temu >>