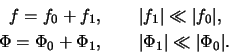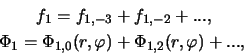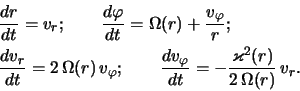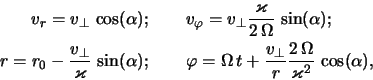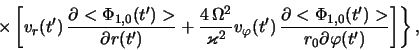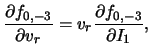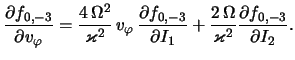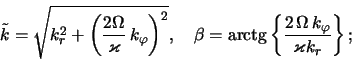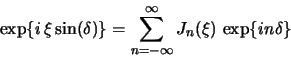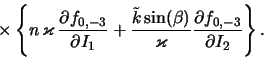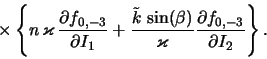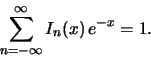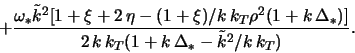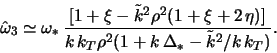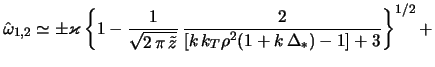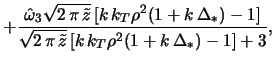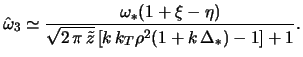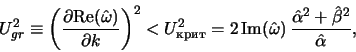---

<< 2.1 Ravnovesie | Oglavlenie | 2.3 Gravitacionnaya neustoichivost' >>

Razdely

• 2.2.1 Postanovka zadachi
• 2.2.2 Vozmushennaya plotnost' zvezdnogo diska
• 2.2.3 Dispersionnoe uravnenie
• 2.2.4 Gravitacionnye i gradientnye neosesimmetrichnye vozmusheniya

---

2.2 Dinamika vozmushenii v ploskosti diska

V predydushem razdele postroena model' stacionarnogo ravnovesnogo zvezdnogo diska. Otkloneniya parametrov diska (funkcii raspredeleniya, potenciala i dr.) ot ravnovesnyh znachenii budem nazyvat' vozmusheniyami toi ili inoi velichiny. Predpolozhenie o maloi velichine amplitud otklonenii ot ravnovesnogo sostoyaniya ves'ma privlekatel'no dlya teoreticheskogo rassmotreniya, poskol'ku ischezaet odna iz glavnyh problem pri reshenii kineticheskogo uravneniya -- ego nelineinost'. Izuchenie vozmozhnyh prostranstvennyh struktur na fone osesimmetrichnogo stacionarnogo sostoyaniya ves'ma populyarno. V to zhe vremya dlya real'nyh sistem predpolozhenie o maloi velichine amplitud vozmushenii chasto narushaetsya. Dostizheniya v postroenii nelineinyh modelei (rech' ne idet o chislennyh, sm. gl. 3) neveliki. Odnako lineinyi podhod pozvolyaet ves'ma uspeshno reshat' klassicheskuyu zadachu ob ustoichivosti ravnovesnoi sistemy, otvechaya na vopros o prichinah rosta so vremenem teh ili inyh pervonachal'no skol' ugodno malyh po amplitude vozmushenii. V osnove analiza lineinoi ustoichivosti lezhit dispersionnoe uravnenie, opredelyayushee vremennuyu dinamiku malyh vozmushenii v zavisimosti ot ih prostranstvennoi struktury. Iz-za stacionarnosti ishodnogo diska vozmusheniya proporcional'ny i budushee sistemy opredelyaetsya nalichiem i znakom mnimoi chasti chastoty (inkrementom). Rost so vremenem amplitudy v sluchae svidetel'stvuet o neustoichivosti sistemy.

V dannom razdele my poluchim dispersionnoe uravnenie, uchityvayushee neodnorodnost' raspredeleniya ravnovesnyh parametrov zvezdnogo diska.

2.2.1 Postanovka zadachi

Sleduya Vandervoortu [192], poluchim kineticheskoe uravnenie, opisyvayushee dinamiku vozmushenii maloi amplitudy v ploskosti tonkogo zvezdnogo diska. Dlya etogo predstavim polnye funkcii raspredeleniya zvezd i gravitacionnyi potencial diska v vide summy ravnovesnyh () i vozmushennyh () velichin:

Linearizovannoe po vozmushennym velichinam , kineticheskoe uravnenie (2.1.7) v epiciklicheskom priblizhenii imeet vid

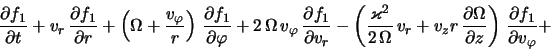
Dlya vychisleniya vozmushennyh velichin , tak zhe, kak i pri opredelenii , , budem ispol'zovat' priblizhenie diska maloi tolshiny ( ). Ochevidno, chto, kak i ravnovesnaya , velichina vozmushennoi poverhnostnoi plotnosti . Poetomu vozmushennaya ob'emnaya plotnost' , i zavisyashaya ot -koordinaty chast' vozmushennogo gravitacionnogo potenciala proporcional'na . V sootvetstvii s etim razlozhim , v ryady po stepenyam malogo parametra [sr. s (2.1.18), (2.1.19)]:

gde i . Togda v ramkah dvuh glavnyh poryadkov po parametru uravnenie (2.2.2) mozhet byt' rasshepleno na sistemu dvuh uravnenii

gde operatory i opredeleny sootnosheniyami (2.1.23) i (2.1.17) sootvetstvenno.

Dlya resheniya etoi sistemy tak zhe, kak i v p. 2.1.2, pereidem k peremennym deistvie-ugol , (2.1.25), (2.1.26). Poskol'ku , gde , to

i uravnenie (2.2.4) priobretaet vid

Obshee reshenie etogo uravneniya v sluchae, esli ravnovesnaya funkciya raspredeleniya opredelena sootnosheniem (2.1.44), mozhno zapisat' v vide

gde simvol oznachaet usrednenie po faze -dvizheniya:

Dlya opredeleniya velichiny usrednim (2.2.5) po faze -dvizheniya v sootvetstvii s pravilom (2.2.9). V rezul'tate poluchim

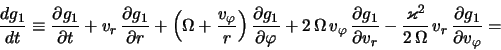
Struktura etogo uravneniya ne opisyvaet effekty, svyazannye s dvizheniem zvezd po -koordinate. Tem samym udaetsya sformulirovat' odin iz etapov resheniya zadachi kak zadachu opredeleniya vozmushennoi funkcii raspredeleniya v modeli tonkogo ( ) zvezdnogo diska. Sootvetstvuyushee vychislenie velichiny , a zatem i vozmushennoi ob'emnoi plotnosti diska konechnoi tolshiny provedeno v sleduyushem punkte.

2.2.2 Vozmushennaya plotnost' zvezdnogo diska

Uravnenie (2.2.10) yavlyaetsya lineinym differencial'nym uravneniem v chastnyh proizvodnyh. Ego harakteristiki, opredelyayushie nevozmushennye traektorii zvezd v ploskosti diska, opisyvayutsya uravneniyami

V ramkah epiciklicheskogo priblizheniya reshenie etih uravnenii imeet vid

gde , -- postoyannye integrirovaniya, , , -- faza dvizheniya zvezdy po epiciklicheskoi traektorii ( -- nachal'naya faza). Iz (2.2.12) netrudno videt', chto nevozmushennoe dvizhenie zvezdy v epiciklicheskom priblizhenii predstavlyaet soboi dvizhenie po ellipsu (epiciklu), odna iz poluosei kotorogo, orientirovannaya na centr diska, ravna , a drugaya, orientirovannaya v azimutal'nom napravlenii, ravna . Centr etogo ellipsa (epicikla) dvizhetsya vokrug centra diska po krugovoi orbite radiusom s uglovoi skorost'yu .

Dlya vychisleniya vozmushennoi funkcii raspredeleniya zapishem uravnenie (2.2.10) v vide, udobnom dlya primeneniya v dal'neishem metoda integrirovaniya po traektoriyam [193]:

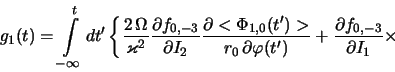
gde ; -- integraly dvizheniya zvezdy v ploskosti diska v epiciklicheskom priblizhenii i uchteno, chto [sm. (2.1.31)]

Predstavlenie v vide (2.2.13) predpolagaet, chto vozmushenie vklyuchaetsya v moment vremeni s amplitudoi prenebrezhimo maloi po sravneniyu s ee urovnem v moment vremeni .

Koefficienty uravneniya (2.2.10) v svyazi so stacionarnost'yu i osesimmetrichnost'yu ravnovesnogo sostoyaniya diska ne zavisyat yavno ot vremeni i azimutal'noi koordinaty. Eto pozvolyaet predstavit' zavisimost' vozmushennyh velichin , ot vremeni i ugla v eksponencial'nom vide , gde -- chastota vozmushenii, -- nomer mody po azimutu, -- azimutal'noe chislo. Takoe predstavlenie, v chastnosti, oznachaet, chto predpolagavshiisya vyshe pri perehode ot (2.2.10) k (2.2.13) rost amplitudy vozmushenii vo vremeni ekvivalenten nalichiyu u chastoty maloi polozhitel'noi mnimoi chasti -- inkrementa.

V radial'nom napravlenii ravnovesnyi zvezdnyi disk neodnoroden. Odnako my mozhem ogranichit'sya rassmotreniem korotkovolnovyh v etom napravlenii vozmushenii -- takih, harakternyi masshtab izmeneniya kotoryh mal po sravneniyu s minimal'nym masshtabom radial'noi neodnorodnosti diska. Rol' poslednego v galaktikah za predelami ih central'nyh oblastei obychno igraet velichina . Dlya izucheniya svoistv takih vozmushenii ispol'zuyut VKB-priblizhenie, v kotorom radial'naya zavisimost' vozmushennyh velichin polagaetsya , gde -- upominavshiisya vyshe harakternyi masshtab izmeneniya vozmushennyh velichin v radial'nom napravlenii ( -- radial'noe volnovoe chislo). Takim obrazom, sformulirovannoe vyshe uslovie primenimosti VKB-priblizheniya mozhno zapisat' v vide^2.6

Takoi podhod pozvolyaet preobrazovat' vse differencial'nye operatory v podyntegral'nom vyrazhenii v (2.2.13) v algebraicheskie i tem samym svyazat' velichiny , , algebraicheskim uravneniem

obychno nazyvaemym dispersionnym. Rezul'taty ego resheniya mozhno traktovat' sleduyushim obrazom. Vozmusheniya, harakterizuemye konkretnymi , , evolyucioniruyut po zakonu , gde -- voobshe govorya, kompleksnaya velichina. I esli korni dispersionnogo uravneniya (2.2.17) pri nekotoryh znacheniyah , takovy, chto , to amplituda takih vozmushenii eksponencial'no rastet so vremenem (voobshe govorya, neobyazatel'no v kazhdoi tochke prostranstva). Zametim takzhe, chto, znaya resheniya (2.2.17), my v obshem sluchae mozhem izuchat' i evolyuciyu proizvol'nyh vozmushenii, esli v nachal'nyi moment vremeni nam budet izvesten fur'e-spektr takogo vozmusheniya v -prostranstve.

Dlya dal'neishego vazhno otmetit', chto my ne svyazyvaem reshenie rassmatrivaemoi zdes' zadachi izucheniya dinamiki malyh vozmushenii v zvezdnom diske s issledovaniem povedeniya kakih-libo global'nyh strukturnyh osobennostei diska (naprimer, spiral'nogo uzora). Poetomu v otlichie ot podhoda Lina i Shu [196,197] ne budem prenebregat' v (2.2.10) i (2.2.13) vozmushennymi azimutal'nymi silami. Takoi podhod pozvolyaet nam izuchit' dispersionnye svoistva neosesimmetrichnyh vozmushenii v neodnorodnom zvezdnom diske i poluchit' uslovie ego ustoichivosti otnositel'no neosesimmetrichnyh vozmushenii v ego ploskosti [198,199].

Vychislim fazu vozmushenii . Dlya etogo pereidem v dvumernom prostranstve volnovyh vektorov (, ) k velichinam

zdes' . Togda s pomosh'yu uravnenii (2.2.12), opisyvayushih nevozmushennye traektorii zvezd, netrudno poluchit'

Ispol'zuya etot rezul'tat, privodim (2.2.13) k vidu

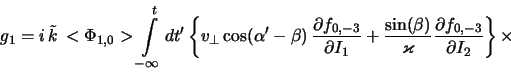
gde ; ; . Zatem s pomosh'yu razlozheniya proizvodyashei funkcii [200]

v ryad po funkciyam Besselya pervogo roda integriruem (2.2.20) po vremeni . V rezul'tate poluchaem

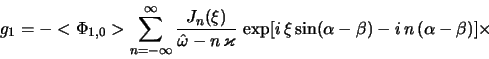
Ob'emnaya plotnost' diska, sozdavaemaya vozmushennoi funkciei raspredeleniya (2.2.8) s opredelyaemoi po (2.2.22) velichinoi , mozhet byt' poluchena integrirovaniem poslednei po prostranstvu skorostei. V sluchae ravnovesnogo diska [sm. (2.1.44)] eta operaciya s uchetom razlozheniya (2.2.21) privodit k sleduyushemu vyrazheniyu:

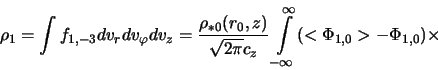
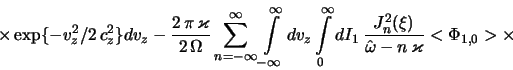
Polyachenko i Fridman [1] pokazali, chto vozmusheniya v ploskosti diska, issledovaniyu svoistv kotoryh i posvyashen etot razdel, v ramkah lineinoi teorii v modeli tonkogo diska otsheplyayutsya ot izgibnyh (membrannyh) kolebanii diska. V poslednih lokal'naya poverhnostnaya plotnost' ne vozmushaetsya, a vozmusheniya ob'emnoi plotnosti imeyut "dipol'nyi" vid. Poetomu pri opisanii svoistv vozmushenii v ploskosti diska v vyrazhenii (2.2.23) neobhodimo otbrosit' chleny, ne dayushie vklada v vozmushennuyu poverhnostnuyu plotnost':

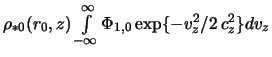Netrudno videt', chto imenno pervyi chlen v (2.2.23) ne daet vklada v . Deistvitel'no, integriruya po -koordinate s uchetom (2.1.45) velichinu , poluchim

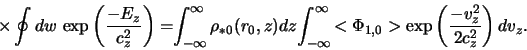
Dlya vychisleniya vozmushennoi ob'emnoi plotnosti, obuslovlennoi vtorym chlenom v (2.2.23), ispol'zuem konkretnyi vid ravnovesnoi funkcii raspredeleniya zvezd (2.1.44). Krome togo, v sootvetstvii s dannymi nablyudenii (sm. razd. 1.1), pokazyvayushimi, chto harakternye tolshiny zvezdnyh diskov galaktik slabo menyayutsya vdol' radial'noi koordinaty, budem schitat' const. V etom sluchae s uchetom (2.1.42) imeem tri nezavisimyh parametra zvezdnogo diska, v kachestve kotoryh vyberem velichiny , , . Togda iz (2.1.35)

Integriruya zatem (2.2.24) po , i otbrasyvaya v sootvetstvii so skazannym vyshe chleny, ne dayushie vklada v vozmushennuyu poverhnostnuyu plotnost' diska, poluchim

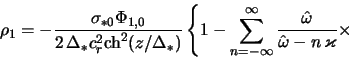
gde ; -- modificirovannye funkcii Besselya pervogo roda,

i uchteno, chto [200]

2.2.3 Dispersionnoe uravnenie

Vozmusheniya plotnosti diska privodyat k vozmusheniyam gravitacionnogo potenciala , i svyaz' mezhdu etimi velichinami opredelyaetsya uravneniem Puassona [sm. (2.1.3)]:

V rassmatrivaemom nami VKB-priblizhenii eto uravnenie dlya garmonik vozmushennogo potenciala, harakterizuemyh volnovym chislom , priobretaet vid

gde velichina opredelyaetsya iz (2.2.28) i tozhdestva

Uravnenie (2.2.34) pohozhe na uravnenie Shredingera, opisyvayushee dvizhenie chasticy v potencial'noi yame vdol' -koordinaty [201]. Odnako dlya (2.2.34) zadacha postavlena neskol'ko po-inomu: dlya fiksirovannogo znacheniya "energii" () neobhodimo naiti "glubinu potencial'noi yamy" ( ), v kotoroi mozhet sushestvovat' zadannyi "uroven' energii" (). Netrudno videt', chto minimal'naya glubina takoi yamy opredelyaetsya bezuzlovoi v -napravlenii sobstvennoi funkciei

a sootvetstvuyushee ei znachenie "glubiny yamy" -- sootnosheniem^2.7

Ispol'zuya zatem etot rezul'tat i opredelenie po (2.2.28), (2.2.35), poluchaem iskomoe dispersionnoe uravnenie, opisyvayushee dinamiku vozmushenii v zvezdnom diske s volnovym vektorom, lezhashim v ego ploskosti:

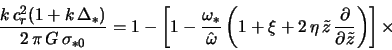
Netrudno videt', chto eto dispersionnoe uravnenie v predele osesimmetrichnyh ( i, sledovatel'no, ) vozmushenii v modeli tonkogo () diska tozhdestvenno sovpadaet s dispersionnym uravneniem Lina i Shu [197] (sm. takzhe v monografii Fridmana i Polyachenko [2]).

2.2.4 Gravitacionnye i gradientnye neosesimmetrichnye vozmusheniya

Issleduem dispersionnye svoistva vozmushenii, opisyvaemyh uravneniem (2.2.38), chastota kotoryh v sisteme otscheta, vrashayusheisya vmeste s veshestvom diska, men'she epiciklicheskoi ( ). Dlya priblizhennogo vychisleniya etih chastot v (2.2.38) mozhno opustit' chleny ryada s . Uproshennoe takim obrazom dispersionnoe uravnenie priobretaet vid

gde ; ; ; .

Esli rassmatrivat' tol'ko osesimmetrichnye vozmusheniya ( i, sledovatel'no, ), to (2.2.39) opisyvaet dve gravitacionnye (dzhinsovskie) vetvi kolebanii zvezdnogo diska, chastoty kotoryh razlichayutsya znakom:

V priblizhenii tonkogo () diska Toomre bylo pokazano, chto takie vozmusheniya ustoichivy [ ] pri vypolnenii usloviya

V tonkom diske, obladayushem dispersiei radial'nyh skorostei , radial'nyi masshtab marginal'no ustoichivyh osesimmetrichnyh vozmushenii mozhet byt' opredelen iz sootnosheniya

Uchet stabiliziruyushego vliyaniya konechnoi tolshiny zvezdnogo diska, predvaritel'nyi analiz kotorogo byl proveden eshe v rabote Toomre [202], pokazyvaet, chto v ramkah modeli (2.1.44) takoi disk ustoichiv pri vypolnenii usloviya [192]

Pereidem k izucheniyu spektra neosesimmetrichnyh vozmushenii. Predvaritel'no zametim, chto . S uchetom togo, chto dlya naibolee blizkih k porogu neustoichivosti vozmushenii v marginal'no ustoichivom po Toomre-Vandervoortu diske , a takzhe usloviya (2.2.16) eto oznachaet, chto dlya takih vozmushenii

V dlinnovolnovoi chasti spektra () v marginal'no ustoichivom po Toomre diske uslovie (2.2.44) tozhe vypolnyaetsya i, sledovatel'no, effekty neodnorodnosti diska maly. V etom predele zakony dispersii dvuh gravitacionnyh vetvei kolebanii zvezdnogo diska soglasno (2.2.39) imeyut vid

Krome etih vetvei dispersionnoe uravnenie (2.2.39) predskazyvaet sushestvovanie eshe odnoi -- gradientnoi vetvi^2.8 neosesimmetrichnyh vozmushenii, zakon dispersii kotoroi imeet vid

Po poryadku velichiny v dlinnovolnovoi () oblasti ; .

V korotkovolnovoi zhe chasti spektra (), ispol'zuya asimptotiku modificirovannyh funkcii Besselya, iz (2.2.39) poluchim

V etoi oblasti dlin voln tozhe ; .

Takim obrazom, kak v dlinnovolnovoi, tak i v korotkovolnovoi chastyah spektra gradientnaya vetv' yavlyaetsya nizkochastotnoi i horosho otdelena ot gravitacionnyh vetvei. Vse tri vetvi v etih chastyah spektra okazyvayutsya ustoichivymi v marginal'no ustoichivom otnositel'no osesimmetrichnyh vozmushenii diske.

Inoi rezul'tat poluchaetsya v promezhutochnoi oblasti dlin voln . Chtoby prodemonstrirovat' eto, rassmotrim prostuyu model' tonkogo () tverdotel'no vrashayushegosya ( ) neodnorodnogo diska, v kotorom (tem samym masshtaby neodnorodnostei i odinakovy i, sledovatel'no, ). V maloi okrestnosti marginal'no ustoichivyh po Toomre vozmushenii s [sm.(2.2.42)] dispersionnoe uravnenie (2.2.39) prinimaet vid

gde ; ; , a velichina v sootvetstvii s dannymi nablyudenii polagalas' ubyvayushei k periferii diska. V (2.2.49) my ogranichilis' razlozheniem chlenov uravneniya (2.2.39) v ryady po stepenyam do vtoroi vklyuchitel'no, imeya v vidu krome vychisleniya chastot kolebanii diska opredelit' eshe i tip neustoichivosti.

Polagaem disk slaboneodnorodnym: . Togda v glavnom poryadke po iz (2.2.49) dlya chastot kolebanii diska sleduet

Neustoichivost' rassmatrivaemoi modeli v oblasti dzhinsovskih dlin voln () ochevidna. V chem zhe ee prichina?

Izvestno, chto v marginal'no ustoichivom po Toomre diske v okrestnosti tochki chastoty obeih gravitacionnyh vetvei osesimmetrichnyh vozmushenii proporcional'ny . Yasno, chto v nekotoroi maloi (v silu ) okrestnosti chastota gradientnyh vozmushenii okazhetsya sravnimoi s chastotoi odnoi iz gravitacionnyh vetvei neosesimmetrichnyh vozmushenii. Togda vzaimovliyanie etih vetvei, iskazhaya spektry vozmushenii, privedet k neustoichivosti neosesimmetrichnyh vozmushenii. Takim obrazom, prichinoi gravitacionno-gradientnoi neustoichivosti (2.2.50) yavlyaetsya neodnorodnost' diska. Priroda zhe etoi neustoichivosti, ochevidno, gravitacionnaya.

Gravitacionno-gradientnaya neustoichivost' prinadlezhit k tipu "absolyutnyh", t.e. takih, pri vozbuzhdenii kotoryh amplituda vozmushenii rastet v kazhdoi tochke prostranstva, dvizhusheisya vmeste s veshestvom diska. Deistvitel'no, neustoichivost' yavlyaetsya "absolyutnoi", a ne "konvektivnoi" (v etom sluchae neustoichivoe vozmushenie snositsya techeniem tak bystro, chto v kazhdoi tochke prostranstva vozmusheniya so vremenem stremyatsya k nulyu), esli vypolnyaetsya uslovie [203]

gde ; . Netrudno videt', chto dlya vozmushenii s i . Tem samym uslovie (2.2.52) dlya gravitacionno-gradientnoi neustoichivosti vypolnyaetsya.

Vpervye gradientnaya vetv' byla poluchena Hanterom [204] v modeli holodnogo () gravitiruyushego diska. Opisannye zdes' rezul'taty otnosyatsya k dostatochno goryachemu ( ) besstolknovitel'nomu disku. Tem ne menee rezul'tat Hantera vytekaet iz dispersionnogo uravneniya (2.2.38) pri vypolnenii cepochki neravenstv (v real'nyh sistemah ).

---

<< 2.1 Ravnovesie | Oglavlenie | 2.3 Gravitacionnaya neustoichivost' >>

Publikacii s klyuchevymi slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Sm. takzhe: Iskrivlennyi disk NGC 4753 Akkrecionnyi disk chernoi dyry: vizualizaciya Dvazhdy iskrivlennyi mir dvoinyh chernyh dyr Spiral'nyi disk vokrug chernoi dyry V centre spiral'noi galaktiki NGC 3521 Massivnaya chernaya dyra razryvaet proletayushuyu zvezdu Ul'trafioletovye kol'ca M31 Vse publikacii na tu zhe temu >>