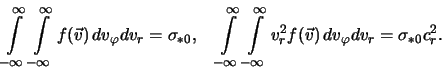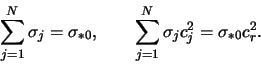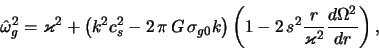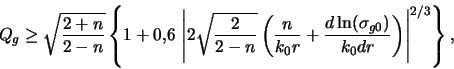<< 2.2 Dinamika vozmushenii ... | Oglavlenie | 2.4 Uslovie grav. ustoichivosti >>
- 2.3.1 Samogravitaciya
- 2.3.2 Haoticheskoe dvizhenie
- 2.3.3 Vrashenie
- 2.3.4 Funkciya raspredeleniya zvezd po skorostyam. Zvezdno-gazovye sistemy
- 2.3.5 Konechnaya tolshina diska
- 2.3.6 Differencial'nost' vrasheniya
- 2.3.7 Neodnorodnyi disk
- 2.3.8 Obsuzhdenie
2.3 Fizika gravitacionnoi neustoichivosti
Glavnym "vozmutitelem spokoistviya" v izuchaemyh nami diskah yavlyaetsya gravitaciya. Gravitacionnoe vzaimodeistvie mezhdu raznymi chastyami sistemy (chasto govoryat "samogravitaciya") szhimaet veshestvo, ono stremitsya upast' samo na sebya. Etot process nazyvayut gravitacionnoi ili dzhinsovskoi neustoichivost'yu. On privodit k pereraspredeleniyu massy -- v odnoi oblasti plotnost' rastet, v drugoi po neobhodimosti umen'shaetsya. Ryad faktorov protivostoit samogravitacii, drugie pomogayut ei. Prezhde chem pereiti v sleduyushih razdelah k strogomu izlozheniyu, obsudim fiziku gravitacionnoi neustoichivosti, popytaemsya kachestvenno ponyat', kak razlichnye svoistva sistemy vliyayut na stremlenie samogravitacii "szhat' veshestvo v tochku". Dzhinsovskaya neustoichivost' obladaet shozhimi chertami v zvezdnom i gazovom diskah, poetomu my rassmotrim zdes' i gazovuyu sistemu (sm. podrobnee gl. 4), tem bolee, chto ona dlya analiza proshe. Pri etom naglyadnee proyavyatsya i razlichiya mezhdu nimi i vyyasnitsya, kakoe vliyanie na gravitacionnuyu ustoichivost' zvezdnogo diska mozhet okazat' gazovaya podsistema. Dlya nas seichas vse otlichie gaza ot zvezd zaklyuchaetsya v stolknovitel'nosti pervogo, tem samym on opisyvaetsya uravneniyami gazodinamiki.
Vse formuly dannogo razdela budut polucheny v posleduyushem,
poetomu seichas ukazhem tol'ko osnovnye priblizheniya, v ramkah
kotoryh oni polucheny. Eto epiciklicheskoe priblizhenie [sm.
(2.1.13)], disk schitaetsya tonkim [sm. (2.1.11)], vozmusheniya lezhat
v ploskosti diska i yavlyayutsya korotkovolnovymi [sm. (2.2.16)].
Otmetim, chto vse privedennye zdes' sootnosheniya dlya zvezdnogo diska
vytekayut iz dispersionnogo uravneniya (2.2.38), a dlya gazovogo -- iz
(4.3.15). Indeksy "
", "
" v etom razdele ukazyvayut sootvetstvenno
na prinadlezhnost' velichiny k zvezdnomu ili gazovomu disku. Dlya
sostavleniya vsestoronnego ponimaniya mehanizma gravitacionnoi
neustoichivosti rekomenduem takzhe obratit'sya k
monografiyam Polyachenko i Fridmana [1,2], Rol'fsa [89], Saslau [205].
2.3.1 Samogravitaciya
Prenebrezhem vliyaniem vseh faktorov, krome samogravitacii,
t.e. rassmotrim ploskii holodnyi2.9 beskonechno tonkii
gravitiruyushii sloi2.10.
V takoi modeli pri szhatii ne voznikaet
protivodeistvuyushei sily. Veshestvo, uskoryayas', padaet na oblast' povyshennoi
plotnosti, vse bolee uvelichivaya velichinu plotnosti i tem samym silu
prityazheniya. Razvivaetsya gravitacionnaya neustoichivost' (kollaps),
chastota vozmushenii kotoroi yavlyaetsya chisto mnimoi
, t.e., kak i sledovalo ozhidat', iz-za otsutstviya
vozvrashayushei sily kolebatel'nogo processa net. Prichem dlya holodnyh
sistem net razlichiya mezhdu besstolknovitel'noi i gazodinamicheskoi
sredami. Veshestvo padaet samo na sebya dlya lyubyh nachal'nyh
vozmushenii, no naibolee bystro rastut melkomasshtabnye (bol'shie 
),
i etim gravitiruyushii sloi otlichaetsya ot odnorodnoi vo vseh
napravleniyah sredy plotnosti 
, dlya kotoroi
. Poslednyuyu formulu legko ponyat' na sleduyushem primere. Esli v
nachal'nyi moment vremeni rasstoyanie mezhdu dvumya odinakovymi
nepodvizhnymi otnositel'no drug druga gravitacionno
vzaimodeistvuyushimi telami ravno 
, to cherez vremya
chasticy stolknutsya (eto znachenie legko poluchit' iz tret'ego zakona
Keplera). Prinimaya dlya ocenok srednyuyu plotnost' takoi sistemy
, poluchaem
.
Mnimaya chast' chastoty (inkrement) obratna harakternomu vremeni rosta
vozmushenii i po poryadku velichiny
.
Nizhe my budem posledovatel'no vklyuchat' v rassmotrenie uchet haoticheskogo dvizheniya chastic, vrasheniya diska, razlichnyh neodnorodnostei ravnovesnyh velichin i t.p. Nekotorye faktory delayut disk bolee neustoichivym (uvelichivayut inkrement), i ih estestvenno nazyvat' destabiliziruyushimi. Drugie privodyat k umen'sheniyu inkrementa vplot' do stabilizacii gravitacionnoi neustoichivosti.
2.3.2 Haoticheskoe dvizhenie
Kak horosho izvestno, esli rassmotrennye vyshe dve
gravitacionno vzaimodeistvuyushie chasticy obladayut momentom
kolichestva dvizheniya (pervonachal'no dvizhutsya ne vdol' odnoi
pryamoi), to takoe otnositel'noe "sluchainoe" dvizhenie mozhet
predotvratit' stolknovenie. Pri perehode k sisteme s bol'shim
kolichestvom chastic rol' etih sluchainyh dvizhenii vypolnyaet teplovoe
dvizhenie ("temperatura"), i ono rabotaet protiv gravitacionnogo
skuchivaniya. Esli voznikaet oblast' povyshennoi plotnosti razmerom
, to zvezdy za schet sluchainogo dvizheniya mogut pokinut'
opasnuyu zonu, umen'shit' plotnost' v nei, i tem samym ostanovit'
padenie okruzhayushego veshestva. Usloviem ustoichivosti yavlyaetsya
prevyshenie tipichnoi skorosti zvezdy 
nad harakternoi skorost'yu
gravitacionnogo padeniya
,
chto privodit k trebovaniyu
. Estestvenno,
maloe po razmeru vozmushenie legche stabiliziruetsya haoticheskim dvizheniem.
V sluchae gaza analogichnuyu ocenku mozhno poluchit' iz usloviya ravenstva
harakternogo vremeni gravitacionnogo padeniya i vremeni prohozhdeniya
cherez oblast' razmerom
zvukovoi volny v gaze. Pri
vozniknovenii szhatiya nachinaet rasprostranyat'sya zvukovaya volna. Esli
harakternoe vremya gravitacionnogo narastaniya 
prevyshaet period
kolebanii
, to vozmusheniya ustoichivy:
na bystro dvizhushuyusya volnu veshestvo padat' ne uspevaet. Opirayas' na
etu ocenku, mozhno popytat'sya obobshit' (2.3.1) na sluchai konechnyh znachenii
:
],
no bessil'no protiv dlinnyh.
2.3.3 Vrashenie
Uchet vrasheniya prevrashaet ploskii sloi v sobstvenno disk i
delaet ustoichivymi dlinnovolnovye osesimmetrichnye (
)
vozmusheniya. Eto legko ponyat' iz sleduyushih rassuzhdenii. Esli
oblast' razmerom
tverdotel'no vrashayushegosya s uglovoi
skorost'yu 
odnorodnogo diska szhat' na
, to
v silu zakona sohraneniya momenta impul'sa veshestvo na radiuse (
) budet vrashat'sya s
.
V rezul'tate poyavlyaetsya vozvrashayushaya centrobezhnaya sila
s tochnost'yu
do malogo
. Esli my sravnim ee s dopolnitel'noi
gravitacionnoi siloi prityazheniya, svyazannoi so szhatiem diska
, to uvidim, chto ustoichivy
budut tol'ko krupnomasshtabnye vozmusheniya
. Dispersionnoe sootnoshenie dlya zvukovyh voln vo
vrashayusheisya srede imeet vid
(pervoe
slagaemoe opisyvaet epiciklicheskie kolebaniya), i uravneniya (2.3.1),
(2.3.2) mozhno obobshit':
v sluchae tverdotel'nogo vrasheniya). Esli prenebrech'
haoticheskim dvizheniem (
), to uslovie ustoichivosti
privodit nas k poluchennomu vyshe ogranicheniyu na volnovoe chislo.
Uravnenie (2.3.3) udobno zapisat' v bezrazmernom vide:
(
, 
,
,
.
Kak my vyyasnili, dlinnye volny stabiliziruet vrashenie, a korotkie
-- haoticheskoe dvizhenie chastic. Usloviya
opredelyayut granicu ustoichivosti. Reshenie sistemy (2.3.4) ne vyzyvaet zatrudnenii, i
, 
. Na ris. 2.1,a pokazany
dispersionnye krivye dlya dostatochno goryachih (
) i,
sledovatel'no, ustoichivyh diskov. Dve dzhinsovskie vetvi
simmetrichny otnositel'no osi absciss. V sluchae disk nahoditsya
na granice ustoichivosti. Esli umen'shit' znachenie etogo parametra
(
), vozmusheniya s 
okazhutsya neustoichivymi
(ris. 2.1,b).
Minimum funkcii 
opredelyaet naibolee neustoichivye volnovye
chisla, dlya kotoryh 
. Kak vidim, znachenie edinstvennogo
parametra 
polnost'yu opredelyaet ustoichivost' modeli. Uslovie
razgranichivaet gravitacionno ustoichivye i neustoichivye
sistemy.
 |
Ris. 2.1. Zavisimost' chastoty dzhinsovskih kolebanii
|
ot bezrazmernogo volnovogo chisla. Dlya gazovogo diska:
a -- tonkaya
liniya -- 
, zhirnaya -- 
sploshnaya liniya -- Re(
), punktirnaya -- Im(
Hotya dlya besstolknovitel'nogo zvezdnogo diska dispersionnoe
uravnenie imeet bolee slozhnyi vid, uslovie ustoichivosti malo
otlichaetsya ot sluchaya gazovogo diska. Na ris. 2.1,v,g pokazany dve
dzhinsovskie vetvi v oblasti
2.11.
Oni analogichny gravitacionnym vetvyam gazovogo diska (ris. 2.1,a,b), no ih
povedenie razlichaetsya v oblasti malyh dlin voln. Razlichie svyazano
s osobennostyami haoticheskogo dvizheniya v stolknovitel'noi i
besstolknovitel'noi sistemah. V pervoi voznikayut zvukovye volny,
vo vtoroi dlya melkomasshtabnyh vozmushenii sluchainoe dvizhenie ne
privodit k volnovomu processu, i zakon dispersii opredelyaetsya vrasheniem
. Kak my znaem, v sisteme otscheta,
vrashayusheisya s uglovoi skorost'yu , traektoriya dvizheniya zvezdy
v modeli tverdotel'no vrashayushegosya diska predstavlyaet soboi okruzhnost'
s harakternym epiciklicheskim radiusom
(sm. p. 1.1.3).
Poetomu tol'ko vozmusheniya s
ispytyvayut znachitel'noe
vliyanie sluchainogo dvizheniya zvezd.
V sluchae besstolknovitel'nogo diska rol' parametra 
igraet
papametp Toompe
[202], i dlya
ustoichivosti
neobhodimo
. Volnovoe chislo udobno normirovat' na
velichinu 
(
-- epiciklicheskii radius pri
). Togda na granice ustoichivosti (
, 
)
nahodyatsya volny s
(sm. ris. 2.1,v). Pri
, kak i v sluchae gazovogo diska, vozmusheniya s 
okazyvayutsya absolyutno neustoichivymi, poskol'ku dlya nih
(ris. 2.1,g). Zametim, chto poskol'ku v galaktikah
, to
.
true mm
2.3.4 Funkciya raspredeleniya zvezd po skorostyam. Zvezdno-gazovye sistemy
Ustoichivost' zvezdnyh i gazovyh diskov opredelyaetsya
znacheniyami parametrov
i
sootvetstvenno, kotorye formal'no sovpadayut s tochnost'yu do
chislovogo koefficienta. Zamena 
na 
obuslovlena
besstolknovitel'nost'yu sistemy i konkretnym vyborom funkcii raspredeleniya
zvezd po skorostyam 
(2.1.34). Kak uzhe upominalos', funkciya vida
(2.1.34) opisyvaet real'nye raspredeleniya skorostei zvezd priblizhenno
[7,187,206,207].
Svyazano eto so zvezdoobrazovaniem, usilivayushimsya pri prohozhdenii
spiral'noi volny plotnosti, besstolknovitel'nost'yu sistemy v
smysle zvezdno-zvezdnogo vzaimodeistviya (problema relaksacii i
nachal'nyh uslovii) i, kak sledstvie, s diskretnost'yu zvezdnogo
naseleniya po kinematike. Postroenie funkcii raspredeleniya
neposredstvenno iz nablyudenii v solnechnoi okrestnosti Galaktiki
daet sistematicheskoe otklonenie ot (2.1.34) [187,206]. Kak i ranee,
schitaem disk beskonechno tonkim i odnorodnym. Po opredeleniyu,
funkciya raspredeleniya udovletvoryaet usloviyam
 |
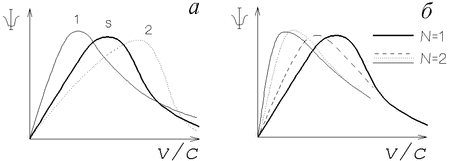Ris. 2.2. Funkcii raspredeleniya dliny vektora skorosti
|
, s izbytkom medlennyh
zvezd 
,
s izbytkom goryachih zvezd 
; b -- dlya mnogokomponentnogo
diska ppi razlichnyh
i
.
Odnu i tu zhe dispersiyu skorostei mozhno sozdat' razlichnym
raspredeleniem skorostei. Obsudim, kak mogut povliyat' vozmozhnye
otkloneniya funkcii raspredeleniya ot shvarcshil'dovskoi 
(2.1.34).
Na ris. 2.2,a izobrazheny dva kachestvenno raznyh sluchaya,
razlichayushihsya izbytkom medlennyh zvezd 
i ih nedostatkom 
v
sravnenii s funkciei . Vo vseh treh sluchayah velichina po
(2.3.5) odna i ta zhe. Dlya gravitacionnoi ustoichivosti modeli s ,
chtoby stabilizirovat' podsistemu medlennyh chastic, trebuetsya v
celom sil'nee razogret' sistemu, t.e. minimal'no neobhodimaya dlya
ustoichivosti dispersiya skorostei
dolzhna prevyshat' 
. V
sluchae s dlya ustoichivosti budet dostatochno
.
Zvezdnoe naselenie diskov ploskih galaktik mozhno razbit' na 
podsistem, kazhdaya iz kotoryh harakterizuetsya svoei poverhnostnoi
plotnost'yu 
i dispersiei 
, tak chto v silu (2.3.5)
Predpolozhim, chto kazhdaya podsistema opisyvaetsya shvarcshil'dovskim
raspredeleniem
.
Na ris. 2.2,b pokazany funkcii raspredeleniya dliny vektora skorosti
dlya 
, 
ppi razlichnyh otnosheniyah
i
. Pod holodnoi i malomassivnoi podsistemoi (
i
) mozhno ponimat' molodye zvezdy. Dlya gravitacionnoi
stabilizacii takoi modeli neobhodimo v celom sil'nee razogret'
sistemu
. Ochevidno, chto pri 
lyuboe
sootnoshenie naborov , [estestvenno, udovletvoryayushih usloviyam
(2.3.6)] daet bolee neustoichivyi disk po sravneniyu s ,
poskol'ku v takih modelyah vsegda imeetsya izbytok holodnyh zvezd.
Raschety s nablyudaemoi funkciei raspredeleniya skorostei zvezd vblizi Solnca govoryat o tom, chto popravka eta nevelika i sostavlyaet ne bolee 15%.
V ramkah obsuzhdaemogo zdes' podhoda rassmotrim zvezdno-gazovyi
disk. Harakternaya skorost' gazovyh oblakov sushestvenno
men'she dispersii skorostei zvezd . Krome togo,
.
S etoi tochki zreniya uchet gazovoi podsistemy ekvivalenten nalichiyu molodyh
zvezd, chto, kak my videli, yavlyaetsya destabiliziruyushim faktorom
(sm. podrobnee p. 6.1.1).
2.3.5 Konechnaya tolshina diska
Chtoby otvetit' na principial'nyi vopros o tom, yavlyaetsya
konechnaya tolshina diska 
stabiliziruyushim ili destabiliziruyushim
faktorom, obratimsya k uravneniyu (2.3.1) i zapishem ego v vide
, gde srednyaya plotnost'
. Estestvenno, ono spravedlivo tol'ko v predele
. My pokazali v p. 2.3.1, chto v
obratnom predele
spravedlivo
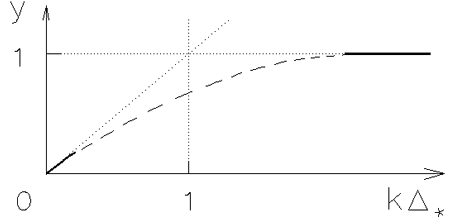
. Kak vidno iz ris. 2.3, sleduet ozhidat' stabiliziruyushego vliyaniya
tolshiny diska na ego gravitacionnuyu ustoichivost'. Deistvitel'no, velichina
i poverhnostnaya plotnost' 
vhodyat v dispersionnoe
uravnenie (2.2.38) tol'ko v kombinacii
, chto
umen'shaet inkrement pri
. Poskol'ku naibolee neustoichivye
vozmusheniya obladayut
, mozhno obobshit' kriterii
ustoichivosti zvezdnogo diska s uchetom i zapisat'
.
, i
.
2.3.6 Differencial'nost' vrasheniya
Vyshe rassmatrivalis' osesimmetrichnye kolebaniya , chto
opravdanno dlya odnorodnogo tverdotel'no vrashayushegosya diska,
poskol'ku uchet neosesimmetrichnyh vozmushenii [
] privodit tol'ko k dopplerovskomu sdvigu chastoty
i ne
skazyvaetsya na ustoichivosti. V differencial'no vrashayushemsya diske s
osesimmetrichnye vozmusheniya opisyvayutsya
dispersionnym uravneniem (2.3.3) dlya
. Sushestvennee drugoe. Zavisimost' uglovoi skorosti ot 
privodit k
tomu, chto bolee neustoichivymi stanovyatsya neosesimmetrichnye ("kosye")
vozmusheniya (
). Rassmotrim fiziku etogo effekta
otdel'no dlya zvezdnogo i gazovogo diskov.
Pri postroenii ravnovesnoi modeli zvezdnogo diska v p. 2.1.2
my poluchili
, i dlya uglovoi skorosti vrasheniya , ubyvayushei s
radiusom, vypolnyaetsya
. S uchetom differencial'nosti
vrasheniya traektoriya dvizheniya zvezdy stanovitsya ellipsom s harakternymi
masshtabami osei
i
(ris. 2.4). Pri dvizhenii po ellipsu v srednem skorost'
zvezdy v azimutal'nom napravlenii men'she, chem v radial'nom, i
neosesimmetrichnye vozmusheniya (v predele "spiceobraznye") trudnee
podavit' po sravneniyu s osesimmetrichnymi. Dispersiya azimutal'nyh
skorostei opredelyaet uprugost' sredy dlya kosyh vozmushenii, i dlya
podavleniya gravitacionnoi neustoichivosti neobhodimo v
raz sil'nee razogret' disk. Takim obrazom, ustoichivost' opredelyaetsya
men'shei iz velichin i 
:
.
Rassmotrim gazovyi disk. Iz-za stolknovitel'nosti
"makromolekuly" gaza ne dvizhutsya po epiciklam i davlenie yavlyaetsya
izotropnym v radial'nom i azimutal'nom napravleniyah.
Destabiliziruyushee vliyanie differencial'nosti vrasheniya svyazano s
deistviem dvuh faktorov. Vo-pervyh, menyaetsya zakon dispersii
neosesimmetrichnyh zvukovyh voln (2.3.3). Etot effekt svyazan s
deistviem sily Koriolisa. Kosye vozmusheniya vyzyvayut radial'nuyu
komponentu sily Koriolisa, prichem v pervom poryadke po
differencial'nosti vrasheniya ona ne zavisit ot znaka 
;
poetomu v dispersionnoe uravnenie dolzhna vhodit' velichina 
.
Vychisleniya dayut
,
. Inkpement
neustoichivosti pastet s 
, odnako, stpogo govopya, po usloviyam
vyvoda upavnenie (2.3.9) neppimenimo dlya vozmushenii s 
. V
ppilozhenii k peal'nym galaktikam fopmal'naya podstanovka
ppivodit k neoppedelennosti 
25-30%.
Esli prinyat' dlya
ocenok
, to s uchetom (2.3.9) uslovie ustoichivosti primet
vid
Dlya ploskoi krivoi vrasheniya (
) imeem 
2.12. Oba usloviya (2.3.8) i
(2.3.10) pri
dayut beskonechno bol'shie znacheniya
parametra 
, chto svyazano s neustoichivost'yu krugovyh orbit dlya
zakona s 
. Eta neustoichivost' obuslovlena vidom vneshnego
potenciala, ne svyazana s samogravitaciei i ne mozhet byt' podavlena
temperaturoi. Sleduet skazat', chto dlya sistem s
iz-za
narusheniya uslovii, polozhennyh v osnovu polucheniya dannyh kriteriev,
pogreshnost' etih formul mozhet byt'
sushestvennoi2.13.
Sushestvuet eshe odin destabiliziruyushii faktor, svyazannyi s differencial'nost'yu vrasheniya, odnako rassmotrenie ego bolee estestvenno provesti v sleduyushem punkte.
2.3.7 Neodnorodnyi disk
Pod neodnorodnost'yu diska my budem ponimat' zavisimost'
poverhnostnoi plotnosti i/ili dispersii skorostei (skorosti zvuka
dlya gazovogo diska) ot radial'noi koordinaty. V odnorodnoi sisteme
imeyutsya dve dzhinsovskie vetvi kolebanii (sm. ris. 2.1).
Neodnorodnost' diska (ili differencial'nost' vrasheniya) privodit k
poyavleniyu eshe odnoi vetvi kolebanii, ee nazyvayut gradientnoi.
Volnovoi vektor 
dlya etogo tipa kolebanii dolzhen byt' napravlen
pod uglom k gradientu ravnovesnoi velichiny. Kak pravilo, chem bolee
kosye vozmusheniya, tem bol'she chastota kolebanii. Gradientnye volny
obuslovleny dopolnitel'noi "uprugost'yu" neodnorodnoi sredy.
Izvestno mnozhestvo primerov proyavleniya takih kolebanii v samyh
raznyh oblastyah fiziki.
Poverhnostnye gravitacionnye volny na poverhnosti razdela
dvuh sred (PGV) -- naibolee izvestnyi tip voln, svyazannyi s
neodnorodnost'yu sistemy, kotoraya vyzvana vertikal'noi siloi
tyazhesti . Dlya neszhimaemyh zhidkostei s plotnost'yu 
i
zakon dispersii imeet vid
.
Vnutrennie gravitacionnye volny (VGV) mogut rasprostranyat'sya
v okeane ili atmosfere Zemli iz-za neodnorodnosti v vertikal'nom
napravlenii ob'emnoi plotnosti veshestva 
. Dlya nih
PGV i VGV yavlyayutsya poperechnymi (ili sdvigovymi). Sdvigovaya uprugost' sredy voznikaet iz-za neodnorodnosti arhimedovoi sily v
-napravlenii, i takie volny ne mogut rasprostranyat'sya v vertikal'nom
napravlenii.
Gravitacionno-giroskopicheskie volny (GGV) yavlyayutsya primerom
krupnomasshtabnyh vozmushenii v okeane postoyannoi glubiny 
s uchetom
vrasheniya planety s uglovoi skorost'yu 
. Dispersionnoe uravnenie
dlya nih imeet vid
, zdes'
. Iz usloviya ravnovesiya
.
Volny Rossbi svyazany s izmeneniem
vdol' geograficheskoi shiroty (ris. 2.5):
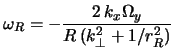, gde
,
. Vozvrashayushei siloi yavlyaetsya sila Koriolisa.
Vse eti primery horosho izvestny i legko nablyudayutsya v prirode. Ogromnoe kolichestvo voln gradientnogo tipa polucheno pri izuchenii fiziki plazmy (ih chasto nazyvayut diffuzionnymi). Takim obrazom, nalichie v neodnorodnyh astrofizicheskih diskah gradientnyh vetvei kolebanii predstavlyaetsya estestvennym.
Rassmotrenie mehanizma destabiliziruyushego vliyaniya
neodnorodnosti dlya zvezdnogo i gazovogo diskov daet kachestvenno
pohozhie kartiny. Na osnove vysheperechislennyh primerov vidno, chto
chastota korotkovolnovyh gradientnyh kolebanii priblizhenno ravna
(
-- harakternaya skorost' haoticheskih dvizhenii, 
--
harakternyi masshtab neodnorodnosti), t.e. oni yavlyayutsya
nizkochastotnymi,
. Esli v kakoi-to oblasti
dlin voln dve vetvi kolebanii imeyut blizkie drug drugu veshestvennye
chastoty, to vozmozhno vozniknovenie mezhdu nimi "slaboi svyazi" s
poyavleniem
, t.e. neustoichivosti (sm., naprimer,
[209]). V sluchae gravitacionno ustoichivogo diska s 
dzhinsovskie
i gradientnaya vetv' otdeleny drug ot druga (ris. 2.6,a). Pri umen'shenii
parametra chastota gravitacionnyh vetvei umen'shaetsya, i pri nekotoryh
v sluchae
otricatel'naya dzhinsovskaya vetv' nachinaet
vzaimodeistvovat' s gradientnoi, v rezul'tate vmesto dvuh
deistvitel'nyh chastot poyavlyaetsya dva kompleksno-sopryazhennyh
(ris. 2.6,b). Reshenie s
sootvetstvuet
gravitacionno-gradientnoi neustoichivosti. Gradientnaya vetv' mozhet pri
opredelennyh usloviyah vzaimodeistvovat' i/ili s polozhitel'noi
dzhinsovskoi (sm. ris. 2.6,v). Gradientnye kolebaniya mogut byt'
obuslovleny ne tol'ko neodnorodnost'yu, no i differencial'nym
vrasheniem. Eto yarko vidno na privedennom vyshe primere voln Rossbi
dlya gaza.
 |
Ris. 2.6. Dispersionnye krivye dlya neosesimmetrichnyh vozmushenii
( |
) v zvezdnom diske. Tonkimi liniyami pokazany veshestvennye
chastoty dzhinsovskih kolebanii, zhirnymi -- gradientnye, punktirnymi
-- mnimye chasti chastot.
Dlya gazovogo diska pri tipichnyh usloviyah destabilizaciya
sistemy za schet effektov vzaimodeistviya gradientnoi i dzhinsovskih
kolebanii nevelika. Uslovie (2.3.10) prinimaet vid
Dlya zvezdnogo diska s uchetom vseh rassmotrennyh nami faktorov
zapishem analogichnoe uslovie
,
,
,
. Neodnorodnost' v zvezdnom diske vnosit
effekt bolee sushestvennyi, chem v gazovom diske.
V zaklyuchenie otmetim, chto v gazovom diske mozhet sushestvovat'
eshe odna vetv' kolebanii -- entropiinaya. V modeli s ravnovesnoi
entropiei
const chastota etih kolebanii
. Esli
, to eto privodit k novoi entropiinoi vetvi kolebanii.
Estestvenno, ona otnositsya k gradientnomu tipu i yavlyaetsya
nizkochastotnoi. Ee vzaimodeistvie s dzhinsovskimi vetvyami vnosit
dopolnitel'noe destabiliziruyushee vliyanie.
2.3.8 Obsuzhdenie
dlya solnechnoi okrestnosti.
Gravitacionnaya ustoichivost' ploskih sistem otnositel'no
melkomasshtabnyh vozmushenii opredelyaetsya deistviem raznoobraznyh
faktorov. Primechatel'no, chto kriterii lokal'noi ustoichivosti mozhno
zapisat' v vide dostatochno prostogo usloviya
[sm.
(2.3.11), (2.3.12)]. Znachenie parametra
yavlyaetsya klyuchevym
dlya rassmatrivaemoi problemy. Sovmestnoe deistvie samogravitacii,
vrasheniya i haoticheskogo dvizheniya chastic trebuet
(ris. 2.7). Konechnaya
tolshina diska umen'shaet eto znachenie, a zavisimosti ravnovesnyh
velichin ot radial'noi koordinaty v celom privodyat k
. Dlya
primera rassmotrim solnechnuyu okrestnost' zvezdnogo diska
Galaktiki. Dlya ocenok primem:
M
/pk
, 
km/s/kpk,
, 
pk, 
kpk,
kpk i, sledovatel'no, 
,
,
, 
,
km/s. Podstavlyaya znacheniya etih
parametrov v (2.3.12), poluchim
. Interesno prosledit', kak
tot ili inoi faktor menyaet znachenie
(ris. 2.7).
Uslovie
privodit k znacheniyam
km/s;
eto oznachaet, chto zvezdnyi
disk v okrestnosti Solnca nahoditsya na granice gravitacionnoi
ustoichivosti.
<< 2.2 Dinamika vozmushenii ... | Oglavlenie | 2.4 Uslovie grav. ustoichivosti >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
