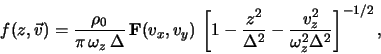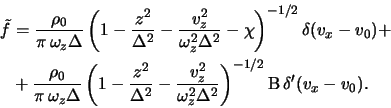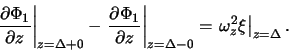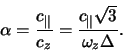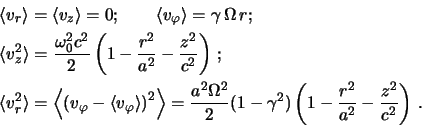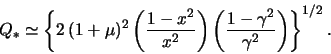<< 2.4 Uslovie grav. ustoichivosti | Oglavlenie | 3. Modelirovanie zvezdnyh diskov >>
- 2.5.1 Dinamika izgibnyh vozmushenii
- 2.5.2 Kakoi dolzhna byt' velichina
 -dispersii skorostei zvezd?
-dispersii skorostei zvezd?
- 2.5.3 Dinamika krupnomasshtabnyh izgibnyh vozmushenii diska, pogruzhennogo v massivnoe galo
2.5 Ustoichivost' diska otnositel'no izgibnyh vozmushenii
2.5.1 Dinamika izgibnyh vozmushenii
V predydushih razdelah byli izucheny dinamika vozmushenii v ploskosti zvezdnogo diska i vytekayushie iz trebovaniya ustoichivosti takih vozmushenii ogranicheniya na parametry diska. V etom razdele my ostanovimsya na drugom tipe vozmushenii -- izgibayushih ploskost' zvezdnogo diska -- i sootvetstvenno naidem te ogranicheniya na parametry diska i sistemy v celom, kotorye vytekayut iz usloviya ustoichivosti takih vozmushenii.
Vpervye, po-vidimomu, dinamika izgibnyh (membrannyh)
kolebanii v modelyah holodnyh tonkih diskov byla rassmotrena v
rabote Hantera i Toomre [231]. Eto issledovanie imelo cel'yu
ob'yasnenie nablyudaemogo v ryade izolirovannyh galaktik
krupnomasshtabnogo iskrivleniya periferii ih diskov. Eshe odna
problema, dlya resheniya kotoroi neobhodimo izuchenie dinamiki
izgibnyh vozmushenii, svyazana s zadachei ob'yasneniya sushestvennogo
razlichiya tolshin i ![]() -dispersii skorostei ob'ektov zvezdnogo i
gazovogo diskov v ploskih galaktikah.
-dispersii skorostei ob'ektov zvezdnogo i
gazovogo diskov v ploskih galaktikah.
Odnako issledovannye Hanterom i Toomre [231] modeli holodnyh tonkih diskov okazalis' ustoichivymi otnositel'no izgibnyh vozmushenii (podrobnoe izlozhenie teorii etogo voprosa sm. v knige Fridmana i Polyachenko [2]). V [232] bylo pokazano, chto dlya resheniya upomyanutyh vyshe problem neobhodimo izuchat' dinamiku izgibnyh vozmushenii v modelyah diskov, goryachih v ih ploskosti.
Ochevidno, chto takie lokal'nye parametry, kak ![]() -dispersiya
skorostei zvezd i tolshina diska, dolzhny opredelyat'sya iz usloviya
ustoichivosti vozmushenii, masshtaby kotoryh maly po sravneniyu s ego
tolshinoi. Sootvetstvuyushee VKB-dispersionnoe uravnenie izgibnyh
vozmushenii v prosteishei modeli odnorodnogo tonkogo nevrashayushegosya
zvezdnogo sloya mozhno zapisat' v vide [233]
-dispersiya
skorostei zvezd i tolshina diska, dolzhny opredelyat'sya iz usloviya
ustoichivosti vozmushenii, masshtaby kotoryh maly po sravneniyu s ego
tolshinoi. Sootvetstvuyushee VKB-dispersionnoe uravnenie izgibnyh
vozmushenii v prosteishei modeli odnorodnogo tonkogo nevrashayushegosya
zvezdnogo sloya mozhno zapisat' v vide [233]
S drugoi storony, izgibnye vozmusheniya, masshtaby kotoryh maly po sravneniyu s tolshinoi diska, takzhe dolzhny byt' ustoichivymi [232]. Eto oznachaet, chto sushestvuet minimal'no neobhodimaya dlya ustoichivosti diska velichina otnosheniya
Dinamika krupnomasshtabnyh izgibnyh vozmushenii, ohvatyvayushih ves' disk, dolzhna, ochevidno, izuchat'sya s uchetom vrasheniya i struktury diska v celom. Takoe issledovanie dlya ryada modelei tonkih diskov [234] pokazalo, chto naibolee krupnomasshtabnye mody mogut byt' neustoichivymi, esli ravnovesie diskov v radial'nom napravlenii obespechivaetsya v osnovnom davleniem (a ne vrasheniem). S umen'sheniem vklada davleniya v uslovie ravnovesiya naibolee krupnomasshtabnye mody stabiliziruyutsya, a bolee korotkovolnovye ostayutsya neustoichivymi. Etot rezul'tat vmeste s dispersionnym uravneniem (2.5.1) pokazyvaet, chto neustoichivost' izgibnyh vozmushenii diska v nekotorom smysle yavlyaetsya dopolnitel'noi k gravitacionnoi neustoichivosti vozmushenii v ploskosti diska. Deistvitel'no, gravitaciya destabiliziruet vozmusheniya v ploskosti diska i stabiliziruet izgibnye; davlenie okazyvaetsya stabiliziruyushim faktorom dlya vozmushenii v ploskosti diska i destabiliziruyushim dlya izgibnyh. Poetomu mozhno bylo by ozhidat', chto samye krupnomasshtabnye izgibnye mody budut, v otlichie ot vozmushenii v ploskosti diska (sm. gl. 3), destabilizirovat'sya dostatochno massivnoi sferoidal'noi podsistemoi. Obsuzhdeniyu etogo voprosa posvyashen p. 2.5.3.
2.5.2 Kakoi dolzhna byt' velichina -dispersii skorostei zvezd?
Opredelim, sleduya Polyachenko i Shuhmanu [235], maksimal'nuyu
anizotropiyu
![]() skorostei v zvezdnom diske. Poskol'ku
vrashenie sushestvenno tol'ko dlya vozmushenii, masshtaby kotoryh
sravnimy s radiusom diska, ishodim iz prostoi modeli
besstolknovitel'nogo nevrashayushegosya ploskogo sloya konechnoi tolshiny
[236], opisyvaemoi funkciei raspredeleniya
skorostei v zvezdnom diske. Poskol'ku
vrashenie sushestvenno tol'ko dlya vozmushenii, masshtaby kotoryh
sravnimy s radiusom diska, ishodim iz prostoi modeli
besstolknovitel'nogo nevrashayushegosya ploskogo sloya konechnoi tolshiny
[236], opisyvaemoi funkciei raspredeleniya
Schitaem vozmusheniya dlinnovolnovymi v tom smysle, chto
harakternyi masshtab vozmusheniya v ploskosti sloya velik po sravneniyu
s ego polutolshinoi (![]() ). Odnako parametr
). Odnako parametr
![]() ne predpolagaem malym. Orientiruem os'
ne predpolagaem malym. Orientiruem os' ![]() vdol'
napravleniya volnovogo vektora. Togda zavisimost'
vdol'
napravleniya volnovogo vektora. Togda zavisimost'
![]() ot
ot ![]() v
nevrashayushemsya sloe stanovitsya nesushestvennoi i zadacha svoditsya k
dvumernoi.
v
nevrashayushemsya sloe stanovitsya nesushestvennoi i zadacha svoditsya k
dvumernoi.
Predstavim funkciyu raspredeleniya po ![]() v vide superpozicii
potokov
v vide superpozicii
potokov
Podstanovka etogo vyrazheniya v linearizovannoe kineticheskoe uravnenie privodit k sleduyushim uravneniyam dlya funkcii
gde
Ocenivaya sootnoshenie velichin B i
gde
Smeshenie granicy sloya ![]() opredelyaem iz usloviya
opredelyaem iz usloviya
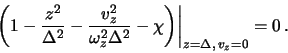
Otsyuda sleduet
Vychislim teper' sootvetstvuyushee (2.5.10) vozmushenie gravitacionnogo potenciala. Dlya etogo sosh'em resheniya uravneniya
pri
Otsyuda s tochnost'yu do chlenov poryadka
Summiruya eto vyrazhenie po vsem potokam, prihodim k iskomomu dispersionnomu uravneniyu:
Dlya konkretnyh vychislenii ishodim iz shvarcshil'dovskoi funkcii
raspredeleniya
![]() . V etom sluchae dispersionnoe uravnenie (2.5.14) privoditsya
k vidu
. V etom sluchae dispersionnoe uravnenie (2.5.14) privoditsya
k vidu
Pri
gde
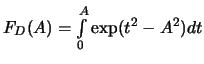 - integral Dosona. Netrudno videt', chto pri
- integral Dosona. Netrudno videt', chto pri
Dannye nablyudenii v okolosolnechnoi okrestnosti Galaktiki ne
protivorechat ocenke (2.5.18) -- soglasno [53,56,57] v srednem po
ne slishkom molodym zvezdam
![]() . Takim obrazom, v
solnechnoi okrestnosti Galaktiki zvezdnyi disk ustoichiv
[soglasno (2.5.18) -- s zapasom] otnositel'no izgibnyh vozmushenii
promezhutochnyh masshtabov
. Takim obrazom, v
solnechnoi okrestnosti Galaktiki zvezdnyi disk ustoichiv
[soglasno (2.5.18) -- s zapasom] otnositel'no izgibnyh vozmushenii
promezhutochnyh masshtabov
![]() (
(![]() - radius diska Galaktiki). To zhe samoe mozhno, po-vidimomu,
utverzhdat' i v otnoshenii zvezdnyh diskov drugih ploskih
galaktik [64,65]. Obsuzhdenie rezul'tatov chislennyh eksperimentov
mozhno naiti v razd. 3.4.
- radius diska Galaktiki). To zhe samoe mozhno, po-vidimomu,
utverzhdat' i v otnoshenii zvezdnyh diskov drugih ploskih
galaktik [64,65]. Obsuzhdenie rezul'tatov chislennyh eksperimentov
mozhno naiti v razd. 3.4.
2.5.3 Dinamika krupnomasshtabnyh izgibnyh vozmushenii diska, pogruzhennogo v massivnoe galo
Dlya izucheniya dinamiki zahvatyvayushih ves' disk ploskoi galaktiki krupnomasshtabnyh izgibnyh mod neobhodimo, ochevidno, uchityvat' strukturu diska i okruzhayushei ego sfericheskoi podsistemy v celom. Analiticheskoe reshenie takoi zadachi vozmozhno tol'ko na dostatochno prostyh modelyah, i v etom razdele my opishem pervye rezul'taty takogo tipa issledovanii [238].
Predstavim model' galaktiki v vide dvuhosnogo tverdotel'no
vrashayushegosya zvezdnogo ellipsoida odnorodnoi plotnosti s poluosyami
![]() ,
, ![]()
![]() , pogruzhennogo v protyazhennoe odnorodnoe sfericheskoe
galo. Ravnovesnyi gravitacionnyi potencial vnutri ellipsoida
(modeli diska) raven
, pogruzhennogo v protyazhennoe odnorodnoe sfericheskoe
galo. Ravnovesnyi gravitacionnyi potencial vnutri ellipsoida
(modeli diska) raven
Ogranichimsya izucheniem dinamiki treh naibolee krupnomasshtabnyh mod:
a) ![]() ("kupol")
("kupol")
v)
gde
Eti mody interesny prezhde vsego kak naibolee krupnomasshtabnye
i potomu, kak pravilo, samye opasnye s tochki zreniya poteri
ustoichivosti. Krome togo, sleduet ozhidat', chto povedenie podobnyh
mod, zahvatyvayushih celikom vsyu sistemu, opredelyaetsya nebol'shim
chislom ee "global'nyh" parametrov. Eto oznachaet, chto issledovanie
ustoichivosti rassmatrivaemoi modeli otnositel'no vozbuzhdeniya
perechislennyh vyshe mod ne potrebuet konkretizacii funkcii
raspredeleniya -- dostatochno lish' budet znat' neskol'ko glavnyh ee
momentov. Dlya rassmatrivaemoi modeli odnorodnogo ellipsoida
vyrazheniya dlya lineinyh i kvadratichnyh po skorostyam momentov
opredelyayutsya odnoznachno, esli tol'ko predpolozhit' izotropiyu v
raspredelenii skorostei v ploskosti vrasheniya. Upomyanutye momenty
imeyut vid
Metod issledovaniya ustoichivosti standarten [2,236]. Snachala
iz uravnenii dlya lagranzhevyh smeshenii ![]() eti velichiny
vyrazhayutsya cherez vozmushennyi potencial
eti velichiny
vyrazhayutsya cherez vozmushennyi potencial ![]() . Zatem vychislyayutsya
vozmusheniya plotnosti i normal'noe smeshenie granicy ellipsoida.
Reshaya zatem uravnenie Puassona i sravnivaya poluchivshiisya potencial
s ishodnym (2.5.20)-(2.5.22), prihodim k sisteme lineinyh
algebraicheskih uravnenii otnositel'no koefficientov, vhodyashih v
vyrazhenie dlya vozmushennogo potenciala. Priravnivaya, nakonec, nulyu
opredelitel' takoi sistemy, poluchaem iskomoe dispersionnoe
uravnenie.
. Zatem vychislyayutsya
vozmusheniya plotnosti i normal'noe smeshenie granicy ellipsoida.
Reshaya zatem uravnenie Puassona i sravnivaya poluchivshiisya potencial
s ishodnym (2.5.20)-(2.5.22), prihodim k sisteme lineinyh
algebraicheskih uravnenii otnositel'no koefficientov, vhodyashih v
vyrazhenie dlya vozmushennogo potenciala. Priravnivaya, nakonec, nulyu
opredelitel' takoi sistemy, poluchaem iskomoe dispersionnoe
uravnenie.
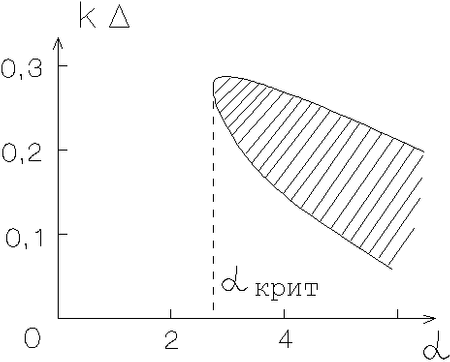
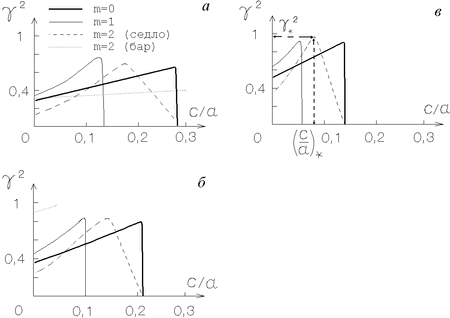 |
Ris. 2.10. Oblasti neustoichivosti izgibnyh mod (2.5.20)
|
Dispersionnye uravneniya dlya ukazannyh vyshe mod (2.5.20) ![]() (2.5.22) reshalis' chislenno (oni dovol'no gromozdki i zdes' ne
privodyatsya). Rezul'taty ih resheniya privedeny na ris. 2.10,a-v,
sootvetstvuyushih razlichnym znacheniyam parametra
(2.5.22) reshalis' chislenno (oni dovol'no gromozdki i zdes' ne
privodyatsya). Rezul'taty ih resheniya privedeny na ris. 2.10,a-v,
sootvetstvuyushih razlichnym znacheniyam parametra ![]() . Iz etih
risunkov vidno, chto v diskovom predele (
. Iz etih
risunkov vidno, chto v diskovom predele (
![]() ) kazhdaya iz mod
neustoichiva pri dostatochno bol'shoi dispersii skorostei zvezd
(oblasti pod krivymi). S uvelicheniem "tolshiny" ellipsoida oblast'
neustoichivosti po parametru
) kazhdaya iz mod
neustoichiva pri dostatochno bol'shoi dispersii skorostei zvezd
(oblasti pod krivymi). S uvelicheniem "tolshiny" ellipsoida oblast'
neustoichivosti po parametru ![]() snachala rastet (t.e. neustoichivymi
stanovyatsya vse bolee "holodnye" sistemy), a zatem dovol'no bystro
ischezaet.
snachala rastet (t.e. neustoichivymi
stanovyatsya vse bolee "holodnye" sistemy), a zatem dovol'no bystro
ischezaet.
Zametim, chto rezkii spad krivyh -- granic oblastei
neustoichivosti na ris. 2.10 proishodit pri takoi splyusnutosti
ellipsoida ![]() , dlya kotoroi v ispol'zuemoi odnorodnoi modeli
imeyutsya rezonansy mezhdu chastotami kolebanii zvezd poperek
ploskosti ellipsoida i v ploskosti ego vrasheniya. Dlya mod
, dlya kotoroi v ispol'zuemoi odnorodnoi modeli
imeyutsya rezonansy mezhdu chastotami kolebanii zvezd poperek
ploskosti ellipsoida i v ploskosti ego vrasheniya. Dlya mod ![]() i
i
![]() est' rezonans
est' rezonans
![]() , a dlya mody
, a dlya mody
![]() -- rezonans
-- rezonans
![]() .
Stol' sil'noe vliyanie etih rezonansov svyazano, ochevidno, s
idealizaciei modeli. Dlya real'nyh differencial'no vrashayushihsya
sistem eti krivye budut imet' bolee gladkii vid.
.
Stol' sil'noe vliyanie etih rezonansov svyazano, ochevidno, s
idealizaciei modeli. Dlya real'nyh differencial'no vrashayushihsya
sistem eti krivye budut imet' bolee gladkii vid.
Kak vidno iz ris. 2.10, moda ![]() (sedlo) sravnitel'no malo
podverzhena vliyaniyu rezonansa. Sushestvenno, odnako, chto imenno eta
moda obladaet samoi bol'shoi oblast'yu neustoichivosti po
(sedlo) sravnitel'no malo
podverzhena vliyaniyu rezonansa. Sushestvenno, odnako, chto imenno eta
moda obladaet samoi bol'shoi oblast'yu neustoichivosti po ![]() pri
pri
![]() . Vazhno takzhe otmetit', chto s uvelicheniem massy galo
oblast' neustoichivosti po parametru splyusnutosti ellipsoida
. Vazhno takzhe otmetit', chto s uvelicheniem massy galo
oblast' neustoichivosti po parametru splyusnutosti ellipsoida
![]() suzhaetsya (neustoichivymi ostayutsya tol'ko sil'no splyusnutye
sistemy). Odnako dlya mody
suzhaetsya (neustoichivymi ostayutsya tol'ko sil'no splyusnutye
sistemy). Odnako dlya mody ![]() dazhe pri ochen' bol'shih znacheniyah
massy galo (
dazhe pri ochen' bol'shih znacheniyah
massy galo (
![]() ) ellipsoid neustoichiv vplot' do
) ellipsoid neustoichiv vplot' do
![]() , t.e. znachenii, harakternyh dlya ploskih podsistem spiral'nyh
galaktik. Tem samym mozhno govorit' o vydelennosti sedloobraznoi
mody sredi drugih mod izgibnogo tipa. Zametim, chto analogichnoe
polozhenie imeet mesto i dlya vozmushenii, ne izgibayushih ploskost'
diska -- zdes' tozhe okazyvaetsya vydelennoi baropodobnaya moda
, t.e. znachenii, harakternyh dlya ploskih podsistem spiral'nyh
galaktik. Tem samym mozhno govorit' o vydelennosti sedloobraznoi
mody sredi drugih mod izgibnogo tipa. Zametim, chto analogichnoe
polozhenie imeet mesto i dlya vozmushenii, ne izgibayushih ploskost'
diska -- zdes' tozhe okazyvaetsya vydelennoi baropodobnaya moda
![]() .
.
V celom naibolee vazhnym rezul'tatom yavlyaetsya obnaruzhenie
zavisimosti polozheniya granic oblastei neustoichivosti ot massy
galo: pri dostatochno bol'shoi masse galo neustoichivymi mogut stat'
sistemy s maloi dispersiei skorostei v ploskosti ellipsoida
[s malym (![]() )]. V etom i sostoit destabiliziruyushaya rol' galo.
)]. V etom i sostoit destabiliziruyushaya rol' galo.
V to zhe vremya s rostom massy galo neobhodimaya dlya
gravitacionnoi ustoichivosti diska dispersiya skorostei zvezd v ego
ploskosti ubyvaet:
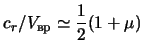 (sm. gl. 3 i ris. 3.8). Poetomu mozhet okazat'sya, chto destabiliziruyushaya
(po otnosheniyu k krupnomasshtabnym izgibnym vozmusheniyam) rol' massivnogo galo ne
proyavitsya. Issleduem etot vopros podrobnee [239,240].
(sm. gl. 3 i ris. 3.8). Poetomu mozhet okazat'sya, chto destabiliziruyushaya
(po otnosheniyu k krupnomasshtabnym izgibnym vozmusheniyam) rol' massivnogo galo ne
proyavitsya. Issleduem etot vopros podrobnee [239,240].
Predpolozhim, chto zvezdnyi disk obladaet zapasom gravitacionnoi ustoichivosti
![]() , kotoryi my opredelim kak otnoshenie nablyudaemoi
, kotoryi my opredelim kak otnoshenie nablyudaemoi ![]() k poluchaemoi
v chislennyh eksperimentah
k poluchaemoi
v chislennyh eksperimentah ![]() [polagaem, chto
[polagaem, chto ![]() sootvetstvuet granice gravitacionnoi ustoichivosti]. Togda vezde za predelami
central'noi chasti diska
sootvetstvuet granice gravitacionnoi ustoichivosti]. Togda vezde za predelami
central'noi chasti diska
gde
Sostoyanie s
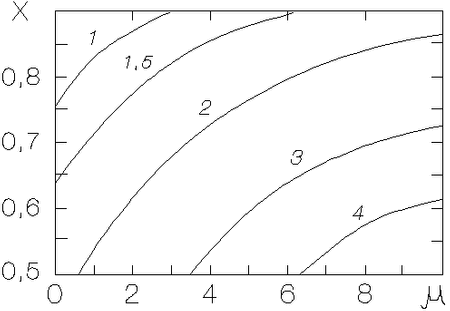 |
Ris. 2.11. Izolinii
parametra
|
Rezul'taty vychislenii velichiny
![]() privedeny na
ris. 2.11 [zametim, chto v ramkah rassmatrivaemoi modeli parametr
privedeny na
ris. 2.11 [zametim, chto v ramkah rassmatrivaemoi modeli parametr
![]() (sm. ris. 2.10) vyhodit pri
(sm. ris. 2.10) vyhodit pri ![]() na asimptoticheskoe
znachenie
na asimptoticheskoe
znachenie
![]() ]. Vidno, chto neustoichivymi okazyvayutsya tol'ko
periferiinye oblasti sistem s malym
]. Vidno, chto neustoichivymi okazyvayutsya tol'ko
periferiinye oblasti sistem s malym ![]() . V sistemah zhe s
. V sistemah zhe s
![]() krupnomasshtabnye izgibnye mody okazyvayutsya zastabilizirovannymi
[oblasti, blizkie k periferii ellipsoida (
krupnomasshtabnye izgibnye mody okazyvayutsya zastabilizirovannymi
[oblasti, blizkie k periferii ellipsoida (
![]() ), ne izuchalis',
poskol'ku v ramkah rassmatrivaemoi modeli v protivorechie s dannymi
nablyudenii oni slishkom holodny:
), ne izuchalis',
poskol'ku v ramkah rassmatrivaemoi modeli v protivorechie s dannymi
nablyudenii oni slishkom holodny: ![]() pri
pri
![]() ]. Takim
obrazom, sleduet ozhidat', chto v galaktikah s dostatochno massivnym galo
neustoichivost' krupnomasshtabnyh izgibnyh mod ne budet proyavlyat'sya.
]. Takim
obrazom, sleduet ozhidat', chto v galaktikah s dostatochno massivnym galo
neustoichivost' krupnomasshtabnyh izgibnyh mod ne budet proyavlyat'sya.
<< 2.4 Uslovie grav. ustoichivosti | Oglavlenie | 3. Modelirovanie zvezdnyh diskov >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |