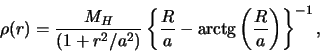<< 3. Modelirovanie zvezdnyh diskov | Oglavlenie | 3.2 Krupnomasshtabnaya struktura ... >>
- 3.1.1 Modeli tipa "chastica-chastica" (PP)
- 3.1.2 Princip postroeniya eksperimental'nyh modelei ploskih galaktik
- 3.1.3 Modeli tipa "chastica-setka" (PM)
- 3.1.4 Ierarhicheskie modeli (TREE-modeli)
3.1 Modeli
Metodov pryamogo laboratornogo modelirovaniya kollektivnyh processov v nepreryvnoi ili diskretnoi gravitiruyushei srede poka ne sushestvuet. Vryad li oni budut razrabotany i v obozrimom budushem. No poyavlenie dostatochno moshnyh EVM otkrylo unikal'nuyu vozmozhnost' chislennogo modelirovaniya takih yavlenii i tem samym sozdalo svoeobraznuyu eksperimental'nuyu bazu dlya fiziki kollektivnyh processov v gravitiruyushih sistemah. V prilozhenii k ploskim galaktikam takoe modelirovanie mozhet imet' cel'yu opredelenie tempa kollektivnyh relaksacionnyh processov i napravleniya evolyucionnyh izmenenii teh ili inyh parametrov diska, vyyasnenie prostranstvennoi struktury kvazistacionarnyh ploskih galaktik i otdel'nyh ih podsistem, a takzhe izuchenie teh processov, kotorye mogli by privesti k obrazovaniyu takih nablyudaemyh struktur, kak spiral'nye uzory, bary, osobennosti vo vzaimodeistvuyushih galaktikah i t.p.
Prakticheski ustoyavshimsya terminom dlya oboznacheniya chislennogo
modelirovaniya gravitiruyushih ![]() tel (kak, vprochem, i
gazodinamicheskih sistem) stalo slovosochetanie "chislennyi (ili
komp'yuternyi) eksperiment". Chislennyi eksperiment v poslednie gody
stanovitsya odnim iz osnovnyh instrumentov v rukah teoretikov pri
izuchenii dinamiki zvezdnyh sistem. Nablyudaetsya bukval'no "zolotaya
lihoradka", harakterizuyushayasya vzryvnym rostom chisla publikacii. V to zhe
vremya, poskol'ku chislo nereshennyh
eshe zadach sushestvenno bol'she rassmotrennyh, to v osnove poluchennyh
rezul'tatov lezhit obychno nebol'shaya seriya raschetov odnoi gruppy
issledovatelei. Kak predstavlyaetsya, imeetsya nasushnaya neobhodimost'
povtoreniya poluchennyh ranee rezul'tatov, chtoby s bol'shim doveriem
k nim otnosit'sya, kak eto i prinyato v eksperimental'noi fizike.
tel (kak, vprochem, i
gazodinamicheskih sistem) stalo slovosochetanie "chislennyi (ili
komp'yuternyi) eksperiment". Chislennyi eksperiment v poslednie gody
stanovitsya odnim iz osnovnyh instrumentov v rukah teoretikov pri
izuchenii dinamiki zvezdnyh sistem. Nablyudaetsya bukval'no "zolotaya
lihoradka", harakterizuyushayasya vzryvnym rostom chisla publikacii. V to zhe
vremya, poskol'ku chislo nereshennyh
eshe zadach sushestvenno bol'she rassmotrennyh, to v osnove poluchennyh
rezul'tatov lezhit obychno nebol'shaya seriya raschetov odnoi gruppy
issledovatelei. Kak predstavlyaetsya, imeetsya nasushnaya neobhodimost'
povtoreniya poluchennyh ranee rezul'tatov, chtoby s bol'shim doveriem
k nim otnosit'sya, kak eto i prinyato v eksperimental'noi fizike.
Obychno ispol'zuyut dva tipa chislennyh modelei zvezdnogo diska: model' "chastica-chastica" (PP); model' "chastica-setka" (PM) i ee razlichnye modifikacii [241,242].
3.1.1 Modeli tipa "chastica-chastica"
(PP)
V modelyah tipa "chastica-chastica" ispol'zuetsya nepreryvnoe
opisanie dvizheniya chastic i v nih uchityvaetsya gravitacionnoe
vzaimodeistvie vseh chastic drug s drugom. Takoi metod, osnovannyi
na pryamom integrirovanii uravnenii dvizheniya dlya sistemy iz
![]() chastic, yavlyaetsya dostatochno prostym dlya ponimaniya i realizacii,
odnako on trebuet bol'shih mashinnyh resursov. Poetomu v modelyah
takogo tipa chislo chastic, kak pravilo, ne prevyshaet
znachenii3.1
chastic, yavlyaetsya dostatochno prostym dlya ponimaniya i realizacii,
odnako on trebuet bol'shih mashinnyh resursov. Poetomu v modelyah
takogo tipa chislo chastic, kak pravilo, ne prevyshaet
znachenii3.1
![]() . Chislo arifmeticheskih deistvii,
neobhodimyh dlya integrirovaniya odnogo vremennogo shaga v ramkah modeli
PP, ravno
. Chislo arifmeticheskih deistvii,
neobhodimyh dlya integrirovaniya odnogo vremennogo shaga v ramkah modeli
PP, ravno
![]() . Netrudno ocenit', chto pri ispol'zovanii
EVM, dlya kotoroi neobhodima 1 mks
na vypolnenie odnoi operacii,
pri
. Netrudno ocenit', chto pri ispol'zovanii
EVM, dlya kotoroi neobhodima 1 mks
na vypolnenie odnoi operacii,
pri ![]() na odin vremennoi shag (a vsego ih trebuetsya, kak pravilo,
neskol'ko tysyach) zatrachivaetsya 10 s, a pri
na odin vremennoi shag (a vsego ih trebuetsya, kak pravilo,
neskol'ko tysyach) zatrachivaetsya 10 s, a pri ![]() bol'she sutok!
bol'she sutok!
Modeli PP ispol'zovalis' v eksperimentah [216-218,243-247] i
mnogih drugih. V etih modelyah, odnako, voznikaet
vopros o velichine masshtaba i haraktere "obrezaniya" gravitacionnogo
vzaimodeistviya chastic na malyh rasstoyaniyah. Delo v tom, chto pri
modelirovanii polnoi galaktiki, sostoyashei iz
![]() zvezd, neobhodimo sozdat' besstolknovitel'nuyu sistemu. Vremya dvoinogo
soudareniya v trehmernoi sisteme ravno [61]
zvezd, neobhodimo sozdat' besstolknovitel'nuyu sistemu. Vremya dvoinogo
soudareniya v trehmernoi sisteme ravno [61]
3.1.2 Princip postroeniya eksperimental'nyh modelei ploskih galaktik
Opishem zdes' dostatochno prostuyu model' s obosnovaniem vybora masshtaba "obrezaniya" gravitacionnogo vzaimodeistviya na malyh rasstoyaniyah.
1. Disk. Zvezdnyi disk polagaem sostoyashim iz N
chastic ravnoi massy. Ispol'zuem sistemu edinic, v kotoroi gravitacionnaya
postoyannaya ![]() , vse chasticy diska raspredeleny v nachal'nyi
moment vremeni vnutri sfery radiusom
, vse chasticy diska raspredeleny v nachal'nyi
moment vremeni vnutri sfery radiusom ![]() i massa diska
i massa diska
![]() (massa kazhdoi chasticy ravna
(massa kazhdoi chasticy ravna ![]() ).
).
Vybrav zakon izmeneniya poverhnostnoi plotnosti ![]() ,
razob'em disk na dostatochno uzkie kol'ca shirinoi
,
razob'em disk na dostatochno uzkie kol'ca shirinoi ![]() i po
zadannomu
i po
zadannomu ![]() vychislim chislo chastic
vychislim chislo chastic ![]() , popadayushih v
, popadayushih v ![]() -e
kol'co. Tak, v "standartnoi" modeli Ostraikera i Piblsa [216]
-e
kol'co. Tak, v "standartnoi" modeli Ostraikera i Piblsa [216]
![]() i chislo
i chislo
![]() , a v modeli
eksponencial'nogo diska [
, a v modeli
eksponencial'nogo diska [
![]() ] chislo chastic v kol'ce
ravno
] chislo chastic v kol'ce
ravno
Kazhdoe kol'co razdelim na ![]() ravnyh chastei v azimutal'nom
napravlenii i v kazhduyu poluchennuyu takim obrazom yacheiku pomestim
chasticu. Koordinaty chasticy vnutri yacheiki estestvenno opredelit' s
pomosh'yu dvukratnogo primeneniya generatora sluchainyh chisel (odin
raz -- v radial'nom napravlenii, vtoroi -- v azimutal'nom),
sopostavlyaya interval izmeneniya sluchainyh chisel (obychno -- [
ravnyh chastei v azimutal'nom
napravlenii i v kazhduyu poluchennuyu takim obrazom yacheiku pomestim
chasticu. Koordinaty chasticy vnutri yacheiki estestvenno opredelit' s
pomosh'yu dvukratnogo primeneniya generatora sluchainyh chisel (odin
raz -- v radial'nom napravlenii, vtoroi -- v azimutal'nom),
sopostavlyaya interval izmeneniya sluchainyh chisel (obychno -- [![]() ]) s
shirinoi kol'ca
]) s
shirinoi kol'ca ![]() i shirinoi sektora
i shirinoi sektora
![]() . Posle etogo v kazhdom kol'ce vychislyaem srednyuyu po
. Posle etogo v kazhdom kol'ce vychislyaem srednyuyu po ![]() chasticam radial'nuyu gravitacionnuyu silu
chasticam radial'nuyu gravitacionnuyu silu ![]() , deistvuyushuyu na kazhduyu
chasticu so storony vseh ostal'nyh chastic diska i staticheskogo galo (sm.
nizhe). I vsem chasticam rassmatrivaemogo kol'ca pridaem azimutal'nuyu
skorost'
, deistvuyushuyu na kazhduyu
chasticu so storony vseh ostal'nyh chastic diska i staticheskogo galo (sm.
nizhe). I vsem chasticam rassmatrivaemogo kol'ca pridaem azimutal'nuyu
skorost'
![]() . Yasno, chto prigotovlennyi takim
obrazom disk yavlyaetsya hotya i ravnovesnym, no "holodnym" i, sledovatel'no,
podverzhennym sil'noi gravitacionnoi neustoichivosti.
. Yasno, chto prigotovlennyi takim
obrazom disk yavlyaetsya hotya i ravnovesnym, no "holodnym" i, sledovatel'no,
podverzhennym sil'noi gravitacionnoi neustoichivosti.
Udovletvoritel'naya ravnovesnaya model' "goryachego" diska
konechnoi tolshiny mozhet byt' postroena na osnove shvarcshil'dovskoi
funkcii raspredeleniya (2.1.34). Dlya etogo dostatochno kakim-libo
obrazom zadat' raspredeleniya dvuh parametrov -- dispersii skorostei
chastic v radial'nom i perpendikulyarnom ploskosti diska
napravleniyah: ![]() ;
; ![]() . Opredelenie pervoi iz
nih estestvenno delat', ispol'zuya rezul'taty teorii gravitacionnoi
ustoichivosti zvezdnogo diska. Dlya etogo, opredeliv epiciklicheskuyu
chastotu3.4
. Opredelenie pervoi iz
nih estestvenno delat', ispol'zuya rezul'taty teorii gravitacionnoi
ustoichivosti zvezdnogo diska. Dlya etogo, opredeliv epiciklicheskuyu
chastotu3.4
![]() na zadannom nabore kolec, nahodim
na zadannom nabore kolec, nahodim
![]() -- dispersiyu radial'nyh skorostei zvezd, neobhodimuyu dlya
podavleniya neustoichivosti osesimmetrichnyh vozmushenii v tonkom diske. I zatem
zadaem velichinu
-- dispersiyu radial'nyh skorostei zvezd, neobhodimuyu dlya
podavleniya neustoichivosti osesimmetrichnyh vozmushenii v tonkom diske. I zatem
zadaem velichinu
![]() . Znachenie parametra
. Znachenie parametra ![]() dolzhno byt', ochevidno, obuslovleno celyami eksperimenta. Tak, v rabotah
[217,218]3.5
dolzhno byt', ochevidno, obuslovleno celyami eksperimenta. Tak, v rabotah
[217,218]3.5
![]() --
v etom sluchae velichina
--
v etom sluchae velichina ![]() primerno ravna
minimal'no neobhodimoi
primerno ravna
minimal'no neobhodimoi ![]() dlya podavleniya gravitacionnoi
neustoichivosti v odnorodnom differencial'no vrashayushemsya tonkom
diske. Opredelennaya takim obrazom velichina
dlya podavleniya gravitacionnoi
neustoichivosti v odnorodnom differencial'no vrashayushemsya tonkom
diske. Opredelennaya takim obrazom velichina ![]() mozhet okazat'sya
slishkom bol'shoi v central'noi chasti diska, gde lokal'nye kriterii
ustoichivosti (2.2.41), (2.4.21) ne primenimy. V etoi oblasti udobno prinyat'
mozhet okazat'sya
slishkom bol'shoi v central'noi chasti diska, gde lokal'nye kriterii
ustoichivosti (2.2.41), (2.4.21) ne primenimy. V etoi oblasti udobno prinyat'
![]() , vybrav
, vybrav
![]() .
.
V sootvetstvii s usloviem ravnovesiya (2.1.36) azimutal'nuyu dispersiyu
skorostei polagaem ravnoi
![]() , a
velichinu dispersii skorostei chastic poperek ploskosti diska
, a
velichinu dispersii skorostei chastic poperek ploskosti diska
![]() [sm. (2.5.18)].
[sm. (2.5.18)].
Dlya modelirovaniya funkcii raspredeleniya (2.1.44) v kazhdom iz treh
![]() napravlenii ishodim iz togo, chto
napravlenii ishodim iz togo, chto
Dlya kazhdoi chasticy generiruem sluchainoe chislo
nahodim
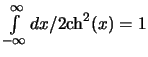 [sm. (2.1.45)]
opredelyaem
[sm. (2.1.45)]
opredelyaem
V rezul'tate vypolneniya vseh etih procedur poluchaem model'
"goryachego" zvezdnogo diska konechnoi tolshiny, v kotoroi neobhodimo
eshe skorrektirovat' koordinaty chastic i ih skorosti takim obrazom,
chtoby centr mass sistemy chastic v hode eksperimenta ostavalsya v
nachale koordinat. Krome togo, neobhodimo eshe skorrektirovat'
skorost' vrasheniya chastic. Deistvitel'no, uslovie radial'nogo
ravnovesiya goryachego diska ne svoditsya k vzaimnoi kompensacii
gravitacionnoi i centrobezhnoi sil. Ego netrudno poluchit',
integriruya s mnozhitelem ![]() stacionarnoe osesimmetrichnoe
(
stacionarnoe osesimmetrichnoe
(
![]() ,
,
![]() ) kineticheskoe uravnenie
(2.1.2) po prostranstvu skorostei:
) kineticheskoe uravnenie
(2.1.2) po prostranstvu skorostei:
2. Galo. Pri postanovke eksperimentov, v kotoryh pomimo diska
ploskoi galaktiki modeliruetsya i ee sfericheskaya podsistema (galo),
neobhodimo uchest', chto dispersiya skorostei zvezd galo znachitel'no
prevyshaet dispersiyu skorostei zvezd diska ([14,98], gl. 1). V to zhe
vremya velichina vozmushenii plotnosti vsyakoi podsistemy obratno
proporcional'na kvadratu ee dispersii skorostei ([197], p. 2.2.2).
Poetomu v processe evolyucii diska, ne menyayushei sushestvenno
raspredelenie mass v nem, galo mozhno schitat' nevozmushayushimsya i
modelirovat' potencialom ![]() , deistvuyushim na zvezdy diska. Eto
podtverdili i neposredstvennye chislennye eksperimenty, provedennye
Holom [248], Selvudom [249], v kotoryh modelirovalis' i disk i
galo. Bylo obnaruzheno, chto galo ostaetsya prakticheski statichnym.
, deistvuyushim na zvezdy diska. Eto
podtverdili i neposredstvennye chislennye eksperimenty, provedennye
Holom [248], Selvudom [249], v kotoryh modelirovalis' i disk i
galo. Bylo obnaruzheno, chto galo ostaetsya prakticheski statichnym.
Potencial ![]() v svoyu ochered' opredelyaetsya raspredeleniem
plotnosti veshestva
v svoyu ochered' opredelyaetsya raspredeleniem
plotnosti veshestva ![]() v galo. Vo mnogih modelyah,
uchityvayushih postoyanstvo skorosti vrasheniya veshestva diska na ego
periferii [29,30], polagayut
v galo. Vo mnogih modelyah,
uchityvayushih postoyanstvo skorosti vrasheniya veshestva diska na ego
periferii [29,30], polagayut
![]() . V sootvetstvii s etim
estestvenna model' galo s raspredeleniem ob'emnoi plotnosti
. V sootvetstvii s etim
estestvenna model' galo s raspredeleniem ob'emnoi plotnosti
V opisannoi vyshe modeli parametr
3. Vzaimodeistvie chastic v diske. Vzaimodeistvie chastic drug
s drugom dolzhno, ochevidno, modelirovat' osnovnye svoistva
zvezdnogo diska kak besstolknovitel'noi gravitiruyushei sistemy.
Konstruktivnoe v eksperimental'nom plane opredelenie
besstolknovitel'nosti diska mozhno sformulirovat' sleduyushim
obrazom: sila, deistvuyushaya na dannuyu chasticu so storony vseh
ostal'nyh chastic diska, dolzhna byt' zametno bol'she sily,
deistvuyushei na tu zhe chasticu so storony ee blizhaishei sosedki. Eto
opredelenie estestvennym obrazom privodit k neobhodimosti
"obrezaniya" gravitacionnogo vzaimodeistviya chastic na malyh
rasstoyaniyah, chto ispol'zovalos' vo vseh chislennyh eksperimentah. Dlya
ocenki velichiny sootvetstvuyushego parametra opredelim "radius
vzaimodeistviya"
![]() sootnosheniem
sootnosheniem
Po dannym nablyudenii v diskah galaktik
Predpolozhim teper', chto "obrezanie" gravitacionnogo vzaimodeistviya na malyh rasstoyaiyah my osushestvlyaem, vychislyaya silu, deistvuyushuyu na
gde
Odnako opisannyi vyshe algoritm vychisleniya sily vzaimodeistviya
mezhdu chasticami pri
![]() [216-218,250]
udovletvoritelen lish' pri izuchenii kollektivnyh processov v
ploskosti diska. Deistvitel'no, pri uslovii sohraneniya
geometricheskogo podobiya eksperimental'nyh modelei real'nym
galaktikam (
[216-218,250]
udovletvoritelen lish' pri izuchenii kollektivnyh processov v
ploskosti diska. Deistvitel'no, pri uslovii sohraneniya
geometricheskogo podobiya eksperimental'nyh modelei real'nym
galaktikam (
![]() ) mozhno nadeyat'sya, chto
pravil'noe modelirovanie kollektivnyh processov poperek ploskosti diska
budet imet' mesto tol'ko v tom sluchae, esli
) mozhno nadeyat'sya, chto
pravil'noe modelirovanie kollektivnyh processov poperek ploskosti diska
budet imet' mesto tol'ko v tom sluchae, esli
![]() . Poskol'ku
. Poskol'ku
![]() , to pri
, to pri
![]() dlya vypolneniya usloviya
dlya vypolneniya usloviya
![]() neobhodimo
neobhodimo
![]() chastic. Sleduet eshe otmetit', chto v
opisannyh vyshe modelyah
ploskih galaktik chislo chastic obychno neveliko. Poetomu poluchennye v hode
obrabotki rezul'tatov znacheniya lokal'nyh parametrov diska ispytyvayut
so vremenem dovol'no zametnye fluktuacii. Odnako esli cel'yu
eksperimenta yavlyaetsya izuchenie harakteristik stacionarnogo diska, to vliyanie
ukazannyh fluktuacii mozhet byt' sushestvenno umen'sheno, esli konechnye
rezul'taty poluchat' posredstvom usredneniya po dostatochno bol'shomu
promezhutku vremeni
chastic. Sleduet eshe otmetit', chto v
opisannyh vyshe modelyah
ploskih galaktik chislo chastic obychno neveliko. Poetomu poluchennye v hode
obrabotki rezul'tatov znacheniya lokal'nyh parametrov diska ispytyvayut
so vremenem dovol'no zametnye fluktuacii. Odnako esli cel'yu
eksperimenta yavlyaetsya izuchenie harakteristik stacionarnogo diska, to vliyanie
ukazannyh fluktuacii mozhet byt' sushestvenno umen'sheno, esli konechnye
rezul'taty poluchat' posredstvom usredneniya po dostatochno bol'shomu
promezhutku vremeni ![]() (poryadka vremeni oborota diska). Pri takom
podhode chislo chastic, effektivno uchastvuyushih v eksperimente,
dostigaet velichiny
(poryadka vremeni oborota diska). Pri takom
podhode chislo chastic, effektivno uchastvuyushih v eksperimente,
dostigaet velichiny ![]() , gde
, gde
![]() (
(![]() -- velichina shaga po vremeni pri integrirovanii sistemy uravnenii
dvizheniya chastic).
-- velichina shaga po vremeni pri integrirovanii sistemy uravnenii
dvizheniya chastic).
3.1.3 Modeli tipa "chastica-setka"
(PM)
V modelyah dannogo tipa konfiguracionnoe prostranstvo i, kak
pravilo, prostranstvo skorostei razbivayutsya na yacheiki, v kotoryh i
lokalizuyutsya chasticy. Neposredstvenno v modeli PM
vzaimodeistvie chastic, nahodyashihsya vnutri odnoi i toi zhe yacheiki
konfiguracionnogo prostranstva, ne uchityvaetsya, a vzaimodeistvie chastic,
nahodyashihsya v razlichnyh yacheikah, modeliruetsya n'yutonovskimi gravitacionnymi
silami, vychislyaemymi, kak pravilo, po koordinatam centrov yacheek.
Tem samym osushestvlyaetsya polnoe "vyklyuchenie" gravitacionnogo
vzaimodeistviya na rasstoyaniyah, men'shih razmera yacheiki (masshtab
"obrezaniya" tozhdestvenno raven razmeru yacheiki). Vzamen, poskol'ku
chislo yacheek ![]() mnogo men'she
mnogo men'she ![]() , imeem vyigrysh v skorosti rascheta,
chto pozvolyaet provodit' chislennye eksperimenty za priemlemoe
mashinnoe vremya s modelyami, soderzhashimi do
, imeem vyigrysh v skorosti rascheta,
chto pozvolyaet provodit' chislennye eksperimenty za priemlemoe
mashinnoe vremya s modelyami, soderzhashimi do
![]() chastic. Modeli etogo tipa podrobno opisany v rabotah [210-213,251-254] i v ryade drugih.
chastic. Modeli etogo tipa podrobno opisany v rabotah [210-213,251-254] i v ryade drugih.
Uchet vzaimodeistviya mezhdu centrami prostranstvennyh yacheek pri bol'shom chisle chastic v kazhdoi yacheike obychno osushestvlyaetsya s ispol'zovaniem diskretnogo analoga teoremy o svertke i algoritma bystrogo preobrazovaniya Fur'e. Principy ucheta sfericheskoi podsistemy (galo+baldzh) i zadaniya nachal'nogo sostoyaniya vpolne shodny dlya metodov PP i PM.
Mozhno postroit' modeli, kotorye otchasti soedinyayut v sebe
bystrotu rascheta metoda PM i uchet blizkodeistvuyushih
sil, kak v modelyah PP. Takogo roda modeli nazyvayut
"chastica-chastica - chastica-setka" (P![]() M) i v osnove ih lezhit
rassheplenie deistvuyushih mezhdu chasticami sil na dve chasti: bystro menyayushuyusya
korotkodeistvuyushuyu chast' i medlenno menyayushuyusya dal'nodeistvuyushuyu [241].
M) i v osnove ih lezhit
rassheplenie deistvuyushih mezhdu chasticami sil na dve chasti: bystro menyayushuyusya
korotkodeistvuyushuyu chast' i medlenno menyayushuyusya dal'nodeistvuyushuyu [241].
Estestvenno, ot postroennyh modelei neobhodimo trebovat' vypolneniya zakonov sohraneniya energii i momenta impul'sa. Na praktike obychno dostigayut tochnosti sohraneniya etih velichin poryadka neskol'kih procentov.
Metod PP s ispol'zovaniem vremennogo usredneniya vpolne prigoden dlya izucheniya global'noi kvazistacionarnoi struktury galaktik. Dlya issledovaniya evolyucionnyh processov bolee priemlemym yavlyaetsya metod PM.
3.1.4 Ierarhicheskie modeli (TREE-modeli)
Dannyi podhod k chislennomu resheniyu gravitacionnoi zadachi ![]() tel predlozhen ne tak davno [255,256]. V osnove metoda lezhit
formirovanie drevovidnoi (TREE) ierarhicheskoi sistemy setok.
Sistema takih setok raspolagaetsya v poryadke podrobnosti ot
naibolee melkih, gde uchityvayutsya naibolee blizkodeistvuyushie sily,
kotorye uchityvayutsya dostatochno tochno, ko vse bolee grubym, na
kotoryh uchityvayutsya dal'nodeistvuyushie sily. Drugimi slovami,
proizvoditsya regulyarizaciya kak dvoinyh sblizhenii, tak i sblizhenii
podsistem na raznyh urovnyah ierarhii. Algoritm trebuet poryadka
tel predlozhen ne tak davno [255,256]. V osnove metoda lezhit
formirovanie drevovidnoi (TREE) ierarhicheskoi sistemy setok.
Sistema takih setok raspolagaetsya v poryadke podrobnosti ot
naibolee melkih, gde uchityvayutsya naibolee blizkodeistvuyushie sily,
kotorye uchityvayutsya dostatochno tochno, ko vse bolee grubym, na
kotoryh uchityvayutsya dal'nodeistvuyushie sily. Drugimi slovami,
proizvoditsya regulyarizaciya kak dvoinyh sblizhenii, tak i sblizhenii
podsistem na raznyh urovnyah ierarhii. Algoritm trebuet poryadka
![]() vychislenii na kazhdom shage integrirovaniya.
vychislenii na kazhdom shage integrirovaniya.
Dostatochno detal'noe opisanie metoda s nekotorymi modifikaciyami dano Dzhernigamom i Porterom [257]. Sravnenie s izvestnymi model'nymi rezul'tatami pokazalo horoshee sootvetstvie, a takzhe podtverdilo preimushestva, svyazannye s zatratami mashinnogo vremeni. TREE-modeli pozvolyayut izuchat' slozhnye sistemy, vklyuchayushie tri vzaimodeistvuyushie komponenty: zvezdnyi i gazovyi diski, "zhivoe" galo [258,259].
Vvedenie v praktiku ierarhicheskih shem fakticheski podvodit
nas k estestvennomu predelu v postroenii chislennyh metodov [260]. V
poslednie gody razvitie poshlo po puti sozdaniya specializirovannyh
komp'yuterov dlya chislennogo resheniya gravitacionnoi zadachi ![]() tel, v
kotoryh vychislenie vzaimodeistviya mezhdu telami realizovano
apparatno [261]. Neposredstvennoe modelirovanie na takogo roda
komp'yuterah govorit ob ih bol'shih vozmozhnostyah [262].
tel, v
kotoryh vychislenie vzaimodeistviya mezhdu telami realizovano
apparatno [261]. Neposredstvennoe modelirovanie na takogo roda
komp'yuterah govorit ob ih bol'shih vozmozhnostyah [262].
Sravnitel'nyi obzor razlichnyyh metodov chislennogo
modelirovaniya ![]() gravitiruyushih tel mozhno naiti, naprimer, v [241,263,264].
gravitiruyushih tel mozhno naiti, naprimer, v [241,263,264].
<< 3. Modelirovanie zvezdnyh diskov | Oglavlenie | 3.2 Krupnomasshtabnaya struktura ... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |