<< 3.3 Gravitacionnaya ustoichivost' ... | Oglavlenie | 3.5 Postroenie ustoichivyh ... >>
- 3.4.1 Rasseyanie na GMO
- 3.4.2 Kollektivnye processy
- 3.4.3 Vliyanie gaza na razvitie bar-mody
- 3.4.4 Pochemu vstrechayutsya tonkie zvezdnye diski?
3.4 Relaksacionnye processy v zvezdnom diske
Obsuzhdeniyu prichin, kotorye mogli by ob'yasnit' nablyudaemuyu korrelyaciyu mezhdu vozrastom, dispersiei skorostei zvezd i ih shkaloi vysot, posvyasheno mnozhestvo rabot (sm., naprimer, monografiyu Marochnika i Suchkova [7] i ssylki tam; razd. 1.1). V dannom razdele obsudim rezul'taty tol'ko nekotoryh chislennyh eksperimentov, kotorye mogli by priblizit' nas k ponimaniyu prirody svyazi mezhdu kinematicheskimi parametrami i ih evolyuciei.
Nablyudeniya svidetel'stvuyut ob evolyucii funkcii raspredeleniya skorostei zvezd. V to zhe vremya zvezdno-zvezdnye sblizheniya v etom smysle zavedomo neeffektivny. Izmenenie skorosti zvezdy v rezul'tate rasseyaniya proporcional'no velichine rasseivayushei massy. Poetomu gigantskie molekulyarnye oblaka (GMO) mogut sluzhit' vazhnym faktorom, vliyayushim na dinamiku zvezdnogo diska. Bol'shie massy i razmery GMO (sm. razd. 1.2) pozvolyayut effektivno rasseivat'sya na nih zvezdam, chto privodit k relaksacionnym processam, uvelichivaya effektivnuyu temperaturu zvezdnogo naseleniya. Rasseyanie na massivnyh netochechnyh ob'ektah (naprimer, GMO) kak vozmozhnyi mehanizm izmeneniya raspredeleniya skorostei zvezd neodnokratno obsuzhdalsya [295-299]. Ego mozhno uslovno nazvat' mehanicheskim v otlichie ot opisannogo v razd. 2.5, gde uzhe rassmatrivalas' problema anizotropii v raspredelenii skorostei zvezd i s tochki zreniya kollektivnyh processov -- ustoichivosti otnositel'no izgibnyh mod. Nizhe obsudim eti dva mehanizma podrobnee.
3.4.1 Rasseyanie na GMO
Privedem nekotorye rezul'taty chislennogo modelirovaniya
dinamiki zvezdnogo diska s uchetom GMO, sleduya rabotam Vilumsena [244,245].
Rassmatrivalas' sleduyushaya model'. Raspredelenie plotnosti
zvezdnogo naseleniya diska vybiralos' v vide [sr. s (2.1.45)]
Raspredeleniyu plotnosti veshestva v GMO
sootvetstvuet potencial
Vzaimodeistvie mezhdu zvezdami i GMO uchityvalos', tol'ko esli rasstoyanie mezhdu nimi ne prevyshalo
kpk. GMO v nachal'nyi
moment obrazovyvali eksponencial'nyi disk s
. Znacheniya
parametrov vybiralis' v prilozhenii k Galaktike:
,
kpk, 
kpk,
, 
kpk, obshaya massa GMO --
. V raschetah var'irovalis' nachal'nye znacheniya
dispersii i parametry GMO. Chislo zvezd 
i GMO 
ne prevyshalo
4000 dlya kazhdoi iz podsistem, tak chto
.
 |
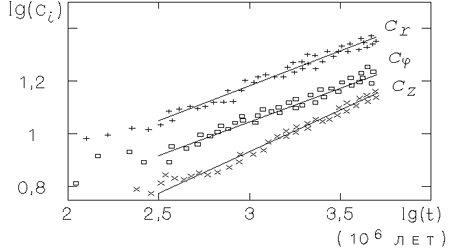Ris. 3.7. Approksimaciya
vremennoi zavisimosti
komponent (
|
)
dispersii skorostei po
rezul'tatam chislennogo
modelirovaniya Vilumsena [
Na ris. 3.7 pokazana dinamika treh komponent dispersii
skorostei zvezd. V konce modelirovaniya poluchaetsya sleduyushee
otnoshenie etih komponent dlya proizvol'noi radial'noi koordinaty:
) vsledstvie
stolknovenii s GMO:
gde
, 
-- poverhnostnaya koncentraciya GMO; 
-- izvestnaya funkciya. Tak kak
, to, sleduya Laseyu,
;
i dlya uslovii eksperimentov
Vilumsena
. Zapishem
reshenie (3.4.6):
Dlya polnoi eksperimental'noi dispersii skorostei (sm. ris. 3.7) i teoreticheskoi zavisimosti (3.4.7) v sluchae
mozhno zapisat'
V tabl.3.1 privedeny znacheniya teoreticheskoi velichiny
i
eksperimental'noi 
dlya raznyh 
[245] s uchetom togo, chto 
zavisit ot radial'noi koordinaty. Kak vidim, v srednem razlichie
mezhdu i sostavlyaet 50%.
| , kpk |
4.2 | 5.1 | 6.0 | 7.0 | 8.1 | 9.3 |
 |
-2.27 | -2.38 | -2.47 | -2.53 | -2.64 | -2.63 |
 |
-2.12 | -2.19 | -2.24 | -2.35 | -2.42 | -2.51 |
 |
1.41 | 1.55 | 1.70 | 1.51 | 1.66 | 1.32 |
V svyazi s nablyudaemoi zavisimost'yu tolshiny zvezdnogo diska ot
vozrasta zvezd upomyanem takzhe o vozrastanii so vremenem v
eksperimentah Vilumsena velichiny 
:
V modelyah Yasumotu i Fudzimoto [299] var'irovalis' v shirokih predelah parametry, opisyvayushie podsistemu GMO, pomimo kotoryh v rassmotrenie vklyuchalis' spiral'nye volny plotnosti. V nachale eksperimentov zvezdnye diski zadavalis' holodnymi i na pervom etape nablyudalsya rezkii rost dispersii skorostei, zatem, nachinaya s
let, nablyudalas' zavisimost' 
s 
. K momentu vremeni 
let v raznyh modelyah polucheno
c
km/s. Dlya
i spiral'noi volny
s uglom zakrutki 
dispersiya dostigala maksimal'nogo znacheniya
(
km/s). Polucheno, chto harakter prostranstvennogo raspredeleniya GMO
slabo vliyaet na temp rosta dispersii skorostei zvezd3.7.
Vremennaya zavisimost' dispersii v solnechnoi okrestnosti
Galaktiki, po dannym Vilena [54], imeet vid ,
(vyvod sdelan ishodya iz dannyh nablyudenii dlya razlichnyh
spektral'nyh klassov zvezd). Kak vidim, dostignutye v
eksperimentah znacheniya
men'she nablyudaemyh dlya
- i 
-tipov zvezd velichin 
km/s.
Sleduet skazat' o tom, chto eshe v 1961 g. Kuzminym [296] byli
polucheny ves'ma blizkie rezul'taty. V ramkah predpolozheniya, chto
gravitacionnoe vzaimodeistvie zvezd s oblakami diffuznoi materii
dolzhno privodit' k rostu kak radial'noi, tak i vertikal'noi
komponent dispersii skorostei zvezd, v ravnovesnom predele (
const) byla poluchena sleduyushaya velichina anizotropii:
, a v differencial'no vrashayushemsya, kak v okrestnosti Solnca
(
), diske dolzhno byt'
.
Itak, esli evolyuciya funkcii raspredeleniya skorostei zvezd
opredelyaetsya processom rasseyaniya zvezd na massivnyh oblakah gaza,
to dlya podsistemy naibolee staryh zvezd diska
. Sleduet, odnako, pomnit', chto rassmotrennye vyshe modeli dostatochno
grubo uchityvayut real'noe raspredelenie v prostranstve rasseivayushih
ob'ektov i ih dinamiku na vremenah, sravnimyh so vremenem zhizni
Galaktiki. V to zhe vremya nadezhnye nablyudaemye znacheniya velichiny
otnosyatsya tol'ko k dostatochno maloi okrestnosti Solnca.
3.4.2 Kollektivnye processy
V dannom punkte obsudim problemu anizotropii dispersii
skorostei zvezd bez privlecheniya massivnyh rasseivayushih ob'ektov.
My uzhe videli, chto soglasno usloviyu ustoichivosti otnositel'no
melkomasshtabnyh izgibnyh vozmushenii
(p. 2.5.2). Zametim, chto etot rezul'tat poluchen v ramkah
modeli odnorodnogo nevrashayushegosya zvezdnogo sloya bez ucheta vliyaniya
sfericheskoi podsistemy, a uchet etih faktorov trebuet chislennogo
modelirovaniya. Dlya izucheniya problemy anizotropii dispersii
skorostei byla postavlena seriya eksperimentov [300], v kotoryh
menyalis' nachal'noe otnoshenie i parametry galo 
i 
v
(3.1.5) s 
. Rassmatrivalos' "ryhloe" yadro sfericheskoi podsistemy (
) i "tochechnoe" yadro (
). V kachestve nachal'nyh uslovii
prinimalos' otnoshenie
, chto sootvetstvuet nablyudaemomu
v Galaktike po vsem zvezdam.
V sistemah s "ryhlym" yadrom galo v techenie pervogo
poluoborota proishodyat bystroe ubyvanie 
i medlennyi rost
, chto privodit issleduemye modeli na granicu ustoichivosti
diska otnositel'no izgibnyh vozmushenii. Uzhe posle pervogo oborota
diska vo vseh modelyah s velichina
. Pri etom okazyvaetsya v srednem blizhe k verhnei
iz ukazannyh granic v modelyah s ne ochen' massivnym galo (
) i blizhe k nizhnei v sisteme s 
. Eshe yarche eto razlichie
mezhdu modelyami s razlichnymi massami sfericheskih podsistem proyavilos' v
sluchae koncentrirovannogo yadra (). Tak, v modelyah s
v srednem vypolnyalos'
, prichem chem blizhe k centru diska i chem
galo malomassivnee, tem s bol'shim zapasom vypolnyaetsya kriterii
ustoichivosti. Otklonenie v bol'shuyu storonu velichiny ot
kriticheskogo znacheniya 
mozhet byt' svyazano s neodnorodnost'yu diska
po 
-koordinate. Deistvitel'no, kriterii (2.5.18) poluchen v modeli
odnorodnogo zvezdnogo sloya s rezkimi granicami. Poetomu pri priblizhenii
k 
vertikal'naya komponenta skorosti stremitsya k nulyu i
tem samym velichina -dispersii okazyvaetsya men'she, chem v modelyah
neodnorodnogo diska, v kotoryh
.
V protivopolozhnost' etomu uchet massy galo mozhet privesti k umen'sheniyu
marginal'nogo znacheniya .
Shodnye rezul'taty byli polucheny v [290], chislennyi
eksperiment kotoryh vklyuchal dostatochno massivnoe (
) i
"ryhloe" (
) galo. V bol'shei chasti diska (
) na protyazhenii vsego
eksperimenta
otnoshenie
ostavalos' prakticheski postoyannym. V to zhe
vremya na dalekoi periferii nablyudalos' nekotoroe umen'shenie dannogo
parametra, vplot' do
.
Poslednii effekt, po-vidimomu, obuslovlen tem, chto v etoi oblasti (
) poverhnostnaya plotnost'
izmenyaetsya ochen' rezko -- masshtab 
umen'shaetsya ot 
kpk do 
kpk. Takaya sil'naya neodnorodnost' diska trebuet
dlya stabilizacii gravitacionnoi neustoichivosti vysokih znachenii
dispersii radial'nyh skorostei 
, tak chto velichina v oblasti
kpk prakticheski perestaet padat' s rostom .
3.4.3 Vliyanie gaza na razvitie bar-mody
V gazovom samogravitiruyushem diske, kak i v zvezdnom, mozhet
razvivat'sya bar-moda3.8. Odnako iz-za stolknovitel'nosti gaza
neustoichivost' (a ona imeet gravitacionnuyu prirodu) proshe
stabilizirovat', v otlichie ot besstolknovitel'nogo zvezdnogo diska
[sm. (3.2.4)] dostatochno vypolneniya
[287]. Vandervoort
[303] v ramkah lineinogo analiza ustoichivosti tverdotel'no
vrashayushegosya odnorodnogo zvezdno-gazovogo sferoida pokazal, chto
kriticheskoe znachenie 
lezhit v predelah
v
zavisimosti ot parametrov modeli i prezhde vsego ot doli massy gaza v sisteme
.
Kak my znaem, galakticheskii gaz yavlyaetsya sil'no neodnorodnoi
na malyh masshtabah sredoi. Nablyudaetsya celaya ierarhiya gazovyh
oblakov, razlichayushihsya svoimi razmerami i massami. V predydushih
punktah my uzhe videli, chto na massivnyh gazovyh oblakah (GMO i
bolee krupnomasshtabnyh obrazovaniyah -- associaciyah) proishodit
effektivnoe rasseyanie, perevodyashee orbital'noe dvizhenie zvezd i
gaza v teplovoe. Takim obrazom, oblachnaya struktura gaza yavlyaetsya
vazhnym faktorom stabilizacii global'nyh mod. Harakternye vremena
obrazovaniya i zhizni oblakov sravnimy so vremenem obrazovaniya bara
(
let). Poetomu dlya vyyasneniya roli gaza v podavlenii
bar-mody neobhodimo detal'noe rassmotrenie processov obrazovaniya
oblakov, ih dinamiku i zvezdoobrazovaniya. Vklad v nagrev diska
daet i dinamicheskoe trenie: pri dvizhenii tyazhelyh gazovyh oblakov
legkie zvezdy ispytyvayut gravitacionnuyu fokusirovku, obrazuya
povyshennuyu koncentraciyu za oblakom.
Nedavnie chislennye eksperimenty, uchityvayushie
vysheperechislennye effekty, naglyadno prodemonstrirovali chrezvychaino
vazhnuyu rol' gaza v dinamike zvezdnogo diska [304,305]. Okazalos',
chto gaz mozhet stabilizirovat' bar-modu, esli on sostavlyaet vsego
neskol'ko procentov ot obshei massy. Razumeetsya, kriticheskoe
znachenie velichiny
zavisit ot mnogochislennyh parametrov
modeli, odnako, po-mneniyu avtorov vysheperechislennyh rabot, dlya
tipichnyh galaktik mozhno prinyat'
(zdes'
sleduet uchityvat' gaz i zvezdy, nahodyashiesya v oblasti formirovaniya bara).
Obsudim podrobnee etot rezul'tat. Dlya raspredeleniya
poverhnostnoi plotnosti v diske
kriterii
ustoichivosti po poryadku velichiny mozhno zapisat' v vide [306]
zdes'
,
,
--
srednyaya skorost' vrasheniya, -- dispersiya radial'nyh skorostei na
radiuse, gde
dostigaet maksimuma. Uchet stolknovitel'nosti gaza
effektivno umen'shaet massu diska 
na velichinu 
. Odnako bolee
sushestvennym faktorom yavlyaetsya razogrev zvezdnoi komponenty na massivnyh
gazovyh oblakah, chto privodit k rostu parametra
so
vremenem v sootvetstvii s formuloi (3.4.7). Harakternyi razmer
gigantskih gazovyh oblakov 
opredelyaetsya gravitacionnoi
neustoichivost'yu i velichina proporcional'na poverhnostnoi
plotnosti gazovogo diska 
(sm. p. 4.3.1). Uchityvaya, chto massa
oblaka
, dlya parametra 
mozhno zapisat'
Kak vidim, nagrev zvezdnoi podsistemy ves'ma sil'no zavisit ot plotnosti gazovogo diska i, kak pokazyvayut chislennye eksperimenty, v sluchae
krupnomasshtabnaya gravitacionnaya
neustoichivost' polnost'yu stabiliziruetsya. Sleduet ne zabyvat', chto
k takomu rezul'tatu privodit sovokupnoe samosoglasovannoe deistvie
fragmentacii gaza, zvezdoobrazovaniya i vseh relaksacionnyh
processov.
3.4.4 Pochemu vstrechayutsya tonkie zvezdnye diski?
Kak otmechalos' v p. 1.1.2, tipichnye znacheniya polutolshiny
zvezdnogo diska sostavlyayut
kpk. Prichem dostatochno
mnogochislenny nablyudaemye s rebra galaktiki s otnosheniem vidimyh
poluosei
. Otnositel'nuyu tolshinu zvezdnogo diska
estestvenno opredelit' otnosheniem
. V sluchae
raspredeleniya ob'emnoi plotnosti
(sm. razd. 1.1) mozhno prinyat'
[104].
Tem samym dlya tonkih zvezdnyh diskov (
) schitaem
. Sleduya rabote [104], opredelim usloviya, pri kotoryh stacionarnye
zvezdnye diski mogut imet' takuyu tolshinu.
Stacionarnaya sistema dolzhna byt', vo-pervyh, gravitacionno
ustoichiva otnositel'no vozmushenii, lezhashih v ploskosti diska, chto
nakladyvaet ogranicheniya na dispersiyu radial'nyh skorostei
V svoyu ochered' polutolshina diska
zavisit ot velichiny 
[sm.
(2.1.42)]. Schitaya, chto sistema nahoditsya na granice ustoichivosti,
iz (3.4.10), (3.4.11), (2.1.41) i (2.2.42) poluchaem
Krugovaya skorost'
v diske opredelyaetsya raspredeleniem
veshestva v ploskoi i sfericheskoi podsistemah, poetomu zapishem
Dlya eksponencial'nogo profilya plotnosti (1.1.2) massa diska
, i v oblasti
skorost'
vrasheniya blizka k svoemu maksimal'nomu znacheniyu
. Primem, chto
(massa galo
nahoditsya vnutri
). V rezul'tate dlya skorosti vrasheniya imeem
Dlya ploskoi krivoi vrasheniya
i
dlya otnositel'noi tolshiny diska mozhem zapisat' [104]
gde
-- chislennyi koefficient (
),
.
Prezhde vsego zametim, chto dlya
parametr
v oblasti
slabo zavisit ot radiusa,
chto ne protivorechit nablyudeniyam.
 |
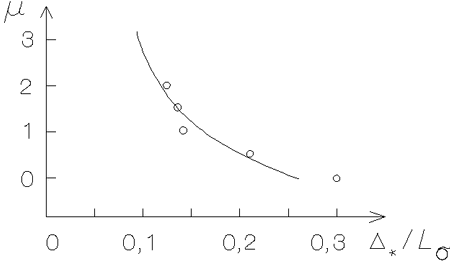Ris. 3.8. Svyaz' mezhdu
otnositel'noi tolshinoi
stacionarnogo zvezdnogo
diska |
v chislennyh eksperimentah.
Liniya sootvetstvuet
zavisimosti
, normirovannoi
po tochke 
.
Iz (3.4.15) vidno, chto s uvelicheniem massy galo polutolshina
zvezdnogo diska umen'shaetsya. Dlya utochneniya dannogo sootnosheniya
obratimsya k rezul'tatam chislennyh eksperimentov, predstavlennym na
ris. 3.8 [104]. Otlichie zavisimosti (3.4.15) ot eksperimental'noi
dlya 
, po-vidimomu, svyazano s plohim vypolneniem epiciklicheskogo
priblizheniya (
), kotoroe lezhit v osnove kriteriya
ustoichivosti, a sledovatel'no, sootnosheniya (3.4.15).
Kak vidim, disk bez galo () imeet
. Dlya
sushestvovaniya tonkih galaktik (
) neobhodimo prisutstvie
sfericheskoi komponenty s 
. Dlya naibolee tonkih
("igloobraznyh") galaktik s
imeem 
.
<< 3.3 Gravitacionnaya ustoichivost' ... | Oglavlenie | 3.5 Postroenie ustoichivyh ... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
