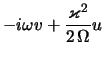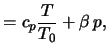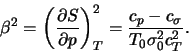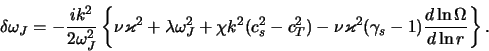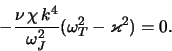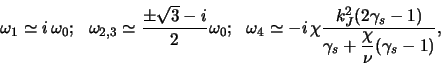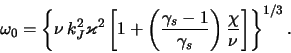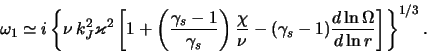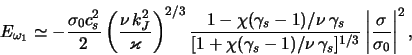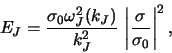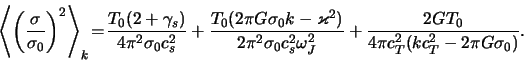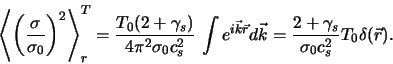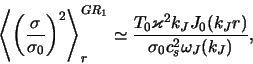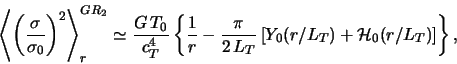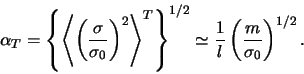---

<< 4.3 Neustoichivosti gazovogo grav... | Oglavlenie | 4.5 Gidrodinamicheskie neustoichivosti ... >>

Razdely

• 4.4.1 Vliyanie dissipacii na gravitacionnye i entropiinye vozmusheniya
• 4.4.2 Bystraya dissipativnaya neustoichivost'
• 4.4.3 Ravnovesnye fluktuacii v gazovom diske

---

4.4 Dissipativnye effekty

Pri reshenii voprosa o gravitacionnoi ustoichivosti gazovogo diska i opredelenii spektra kolebanii v ego ploskosti uchet dissipativnyh chlenov v pervom priblizhenii nesushestven. Eto mozhno proillyustrirovat' sleduyushei ocenkoi. Velichina harakternoi "vyazkoi" chastoty s po parametram gazovogo diska Galaktiki v okrestnosti Solnca (zdes' -- molekulyarnaya kinematicheskaya vyazkost'). V to zhe vremya epiciklicheskaya chastota s .

Tem ne menee issledovanie effektov, svyazannyh s uchetom dissipativnyh chlenov, mozhet privesti k vazhnym rezul'tatam. Vo-pervyh, potomu, chto nekotorye tipy vozmushenii v ploskosti gazovogo diska mogut obladat' otricatel'noi energiei [2] i, sledovatel'no, byt' dissipativno neustoichivymi dazhe v gravitacionno ustoichivom diske. Vo-vtoryh, uchet dissipativnyh chlenov pozvolyaet v principe opredelit' uroven' ravnovesnyh fluktuacii, pol'zuyas' fluktuacionno-dissipativnoi teoremoi [221,339]. Hakonec, melkomasshtabnuyu tupbulentnost' mozhno uchityvat' v pamkah dissipativnoi modeli s effektivnoi (tupbulentnoi) vyazkost'yu (sm. p. 5.1.1).

4.4.1 Vliyanie dissipacii na gravitacionnye i entropiinye vozmusheniya

Ispol'zuem priblizhenie tonkogo diska i ogranichimsya izucheniem korotkovolnovyh osesimmetrichnyh vozmushenii. Dlya takih vozmushenii fur'e-garmoniki linearizovannyh uravnenii gazodinamiki s uchetom dissipativnyh chlenov imeyut vid [329] [sp. s (4.2.14)-(4.2.17)]

gde ; , -- pervaya i vtoraya kinematicheskie vyazkosti, -- vozmushenie entpopii, -- koefficient temperaturoprovodnosti, -- udel'naya teploemkost' pri postoyannoi plotnosti.

Sistema (4.4.1)-(4.4.4) dolzhna byt' dopolnena uravneniem Puassona, korotkovolnovoe reshenie kotorogo imeet vid , i dvumya termodinamicheskimi sootnosheniyami

gde -- udel'naya teploemkost' pri postoyannom davlenii i

Reshaya privedennuyu vyshe sistemu algebraicheskih uravnenii, poluchim dispersionnoe uravnenie, opisyvayushee svoistva rassmatrivaemyh vozmushenii

gde ; . V bezdissipativnom priblizhenii iz (4.4.8) poluchaem dispersionnoe uravnenie osesimmetrichnyh gravitacionnyh vozmushenii

Vyyasnim teper' vliyanie dissipacii na eti vozmusheniya. V sootvetstvii s privedennymi vyshe ocenkami polagaem , gde . Togda v lineinom po dissipativnym koefficientam priblizhenii poluchaem ( ; )

Poskol'ku , i v diskah ploskih galaktik , to v gravitacionno ustoichivom diske ( ) dzhinsovskie vozmusheniya zatuhayut, a v gravitacionno neustoichivom diske ( ) ispytyvayut dopolnitel'nuyu destabilizaciyu iz-za dissipativnyh effektov. Etot rezul'tat kazhetsya estestvennym, tak kak dzhinsovskie vozmusheniya predstavlyayut soboi zvukovye () vozmusheniya s uchetom giroskopicheskih effektov () i samosoglasovannyh vozmushenii gravitacionnogo potenciala ( ). Zvukovye zhe vozmusheniya zatuhayut [327]

i etot rezul'tat netrudno poluchit' iz (4.4.9) v predele korotkovolnovyh () vozmushenii.

Obshee dispersionnoe uravnenie (4.4.8) -- uravnenie chetvertoi stepeni po . V bezdissipativnom priblizhenii iz nego sleduet, chto krome dzhinsovskih , sushestvuet eshe dva (entropiinyh) tipa vozmushenii s . S uchetom dissipacii, polagaya , dlya etih vozmushenii iz (4.4.8) poluchaem uproshennoe (kvadratnoe po ) dispersionnoe uravnenie

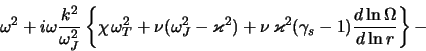
Esli prenebrech' teploprovodnost'yu ( ) i schitat' disk tverdotel'no vrashayushimsya, to iz (4.4.11) sleduyut rezul'taty rabot [340,341]

i, sledovatel'no, v gravitacionno ustoichivom ( ) gazovom diske mozhet razvivat'sya dissipativnaya neustoichivost' v oblasti dlin voln ^4.3. Uchet konechnoi teploprovodnosti rasshiryaet interval dissipativno neustoichivyh dlin voln [329] do

Etot rezul'tat kachestvenno soglasuetsya s poluchennym Kumarom [342] dlya modeli gravitiruyushego cilindra.

4.4.2 Bystraya dissipativnaya neustoichivost'

Iz dispersionnogo uravneniya (4.4.11) sleduet, chto inkrement dissipativnoi neustoichivosti po poryadku velichiny raven . Netrudno takzhe videt', chto uchet differencial'nosti vrasheniya diska ne menyaet poryadok velichiny etogo rezul'tata. Eti rezul'taty, odnako, mozhno schitat' korrektnymi tol'ko v tom sluchae, esli harakternoe vremya nestacionarnosti diska mnogo bol'she obratnogo inkrementa. Harakternoe vremya dinamicheskoi nestacionarnosti , a harakternoe vremya teplovoi nestacionarnosti (eta ocenka vytekaet iz uravneniya balansa tepla). V obshem sluchae inkrement dissipativnyh vozmushenii poryadka i . Otsyuda netrudno videt', chto . Takim obrazom, harakternye vremena teplovoi nestacionarnosti diska i razvitiya dissipativnoi neustoichivosti okazyvayutsya odnogo poryadka.

V svyazi so skazannym vyshe obratim vnimanie na sleduyushee obstoyatel'stvo [343]. Inkrement dissipativnoi neustoichivosti (ravno kak i dekrement zatuhaniya gravitacionnyh vozmushenii) po poryadku velichiny raven za predelami dovol'no uzkoi zony volnovyh chisel, lezhashei v okrestnosti . No dlya blizkogo k granice gravitacionnoi ustoichivosti diska v predelah ukazannoi zony volnovyh chisel inkrement dissipativnoi neustoichivosti okazyvaetsya poryadka . Yasno, chto v takom diske vozmozhno , ili inache

i, sledovatel'no, privedennye vyshe rezul'taty v maloi okrestnosti budut neprimenimy. V etom sluchae termin "gravitacionnye vozmusheniya" teryaet smysl i dispersionnye svoistva vseh chetyreh tipov vozmushenii dolzhny opredelyat'sya iz obshego dispersionnogo uravneniya (4.4.8), resheniya kotorogo pri i imeyut vid (bez ucheta differencial'nosti vrasheniya diska)

gde

Iz etogo spektra reshenii neustoichivymi yavlyayutsya tol'ko vozmusheniya s i ih inkrement

a ostal'nye resheniya sootvetstvuyut zatuhayushim vozmusheniyam.

Uchityvaya tot fakt, chto po poryadku velichiny i ( -- dlina svobodnogo probega chastic), netrudno videt', chto . Poetomu dissipativnaya neustoichivost' (4.4.14) yavlyaetsya bystroi i dlya dinamicheskih processov, opredelyaemyh etoi neustoichivost'yu, teplovaya nestacionarnost' diska nesushestvenna.

Netrudno obobshit' rezul'tat (4.4.14) i na sluchai differencial'no vrashayushegosya diska. V predele iz ishodnogo dispersionnogo uravneniya (4.4.8) poluchaem

Poskol'ku i dlya astrofizicheskih diskov , to netrudno videt', chto po poryadku velichiny inkrement (4.4.16) okazyvaetsya takim zhe, kak v sluchae tverdotel'nogo vrasheniya. Takim obrazom, uchet differencial'nosti vrasheniya diska ne vnosit nichego principial'no novogo v dinamiku dissipativnoi neustoichivosti.

V naibolee korotkovolnovom predele [sm. (4.4.12)] dissipativnaya neustoichivost' ne imeet mesta. Eto estestvennym obrazom navodit na mysl', chto dissipativnaya raskachka vozmushenii v gravitacionno ustoichivom diske obuslovlena vliyaniem vozmushenii gravitacionnogo polya, sushestvennym v oblasti dlin voln . Kak pokazali Fridman i Polyachenko [2], eto vliyanie proyavlyaetsya v tom, chto plotnost' energii dissipativno neustoichivyh vozmushenii yavlyaetsya otricatel'noi ( ). V etom sluchae dissipaciya energii vozmushenii ( ) ekvivalentna rostu ee absolyutnoi velichiny i, sledovatel'no, rostu amplitudy vozmusheniya. Deistvitel'no, dlya dissipativno neustoichivyh vozmushenii (4.4.14) s chastotoi [343]

gde -- vozmushennaya poverhnostnaya plotnost' diska.

Analogichnye vychisleniya plotnosti energii gravitacionnyh vozmushenii pri privodyat k sleduyushemu rezul'tatu:

otkuda vidno, chto . Poetomu dzhinsovskie vozmusheniya s uchetom dissipativnyh faktorov v gravitacionno ustoichivom diske zatuhayut i dopolnitel'no neustoichivy v gravitacionno neustoichivom diske [sm. (4.4.9)].

4.4.3 Ravnovesnye fluktuacii v gazovom diske

Dlya vychisleniya urovnya ravnovesnyh shumov v gravitiruyushem gazovom diske ispol'zuem fluktuacionno-dissipativnuyu teoremu [221] i gidrodinamicheskuyu teoriyu fluktuacii [339]. Dlya prostoty ogranichimsya model'yu odnorodnogo tverdotel'no vrashayushegosya ( ) diska i, rassmatrivaya korotkovolnovye vozmusheniya, orientiruem os' "" vdol' napravleniya volnovogo vektora . Fur'e-garmoniki gazodinamicheskih uravnenii s uchetom storonnih sil, vvodimyh dlya vychisleniya tenzora obobshennoi vospriimchivosti vo vrashayusheisya vmeste s diskom sisteme otscheta, imeyut vid [344]

gde , , . Eta sistema dolzhna byt' dopolnena termodinamicheskimi sootnosheniyami (4.4.5), (4.4.6) i uravneniem Puassona ( ). Uchet dissipativnyh chlenov v (4.4.19)-(4.4.22) neobhodim dlya obhoda polyusov v kompleksnoi -ploskosti pri obratnom fur'e-preobrazovanii spektral'noi plotnosti shumov. V okonchatel'nyi otvet -- velichinu urovnya shumov -- dissipativnye koefficienty ne voidut, poskol'ku . Poetomu dlya uprosheniya vychislenii polozhim .

Dissipaciya energii v gazovom diske pod deistviem storonnih sil opredelyaetsya vyrazheniem

gde integrirovanie provoditsya po poverhnosti diska, a , -- obobshennye koordinaty i storonnie sily, spektral'naya svyaz' mezhdu kotorymi opredelyaetsya sootnosheniem [221]

gde -- tenzor obobshennoi vospriimchivosti.

V kachestve obobshennyh koordinat vyberem velichiny , , . Togda (). Ispol'zuya eti opredeleniya i reshaya privedennuyu vyshe sistemu, mozhno poluchit' komponenty tenzora obobshennoi vospriimchivosti. Ispol'zuya osnovnuyu formulu fluktuacionno-dissipativnoi teoremy [221], zapisannuyu dlya ploskogo sluchaya

spektral'nyi uroven' fluktuacii poverhnostnoi plotnosti mozhno predstavit' v vide [344]

Zdes' ne zavisyashii ot volnovogo chisla pervyi chlen -- spektral'naya plotnost' termodinamicheskih shumov, a vtoroi i tretii chleny mozhno nazvat' spektral'noi plotnost'yu "gravitacionno-vrashatel'nyh" shumov. Vychislyaya korrelyacionnuyu funkciyu termodinamicheskih shumov, poluchaem

Otsutstvie prostranstvennoi korrelyacii termodinamicheskih shumov sleduet rassmatrivat' kak ukazanie na to, chto harakternyi razmer korrelyacii v etom sluchae okazyvaetsya poryadka minimal'no vozmozhnogo v gidrodinamike razmera -- dliny svobodnogo probega chastic . Takim obrazom, v (4.4.27) sleduet polagat' .

Spektral'naya plotnost' "gravitacionno-vrashatel'nyh" shumov, predstavlennaya vtorym v (4.4.26) chlenom, v diske, blizkom k granice gravitacionnoi ustoichivosti [ ], imeet rezkii maksimum v okrestnosti , gde . S uchetom etogo obstoyatel'stva poluchaem

gde -- funkciya Besselya pervogo roda. Nakonec, integrirovanie poslednego v (4.4.26) chlena daet

gde , , -- funkcii Neimana i Struve sootvetstvenno.

Poluchim sootnosheniya dlya ocenok urovnya shumov. Poskol'ku , gde -- harakternaya massa "chastic" diska, to dlya termodinamicheskih shumov (4.4.27) s uchetom togo, chto , poluchaem

Dlya netermodinamicheskih fluktuacii (4.4.28) harakternyi prostranstvennyi masshtab , a ih intensivnost' v masshtabah s uchetom rezul'tata (4.4.14) mozhet byt' ocenena kak

Nakonec, harakternyi masshtab netermodinamicheskih shumov (4.4.29) poryadka , a ih maksimal'naya intensivnost' (pri )

V kachestve primera primeneniya izlozhennoi vyshe teorii ocenim uroven' ravnovesnyh shumov v solnechnoi okrestnosti gazovoi podsistemy Galaktiki. Budem schitat', chto dispersiya skorostei gazovyh oblakov -- "makroatomov" diska km/s, ih harakternye radius i massa ravny pk i M sootvetstvenno. Ispol'zuya takzhe dannye o parametrah gazovogo diska v okrestnosti Solnca: s; M/pk; pk, poluchaem pk, chislo oblakov v edinice ob'ema pk. Poskol'ku gazovye oblaka -- otnyud' ne tverdye sfery, schitaem, chto effektivnyi (stolknovitel'nyi) radius srednego oblaka neskol'ko men'she nablyudaemogo (pust' ). Togda sechenie vzaimodeistviya oblakov pk, a dlina svobodnogo probega pk. V rezul'tate poluchaem

Vysokii uroven' shumov, predskazyvaemyi etimi ocenkami, oznachaet, chto fluktuacionnye struktury v gazovoi podsisteme Galaktiki mogut byt' v principe nablyudaemymi. Harakternye razmery naibolee intensivnyh iz etih struktur (termodinamicheskih) okazyvayutsya poryadka dliny svobodnogo probega oblakov (neskol'kih mezhoblachnyh rasstoyanii), i takie kompleksy mogut soderzhat' do neskol'kih desyatkov oblakov. Neskol'ko menee intensivnye netermodinamicheskie fluktuacii imeyut harakternye razmery (po parametram gazovoi podsistemy v okrestnosti Solnca eto kpk i mogut, po-vidimomu, obespechit' zatravochnye vozmusheniya dlya teh ili inyh osobennostei spiral'nogo uzora (otvetvleniya ot spiralei i t.p.).

---

<< 4.3 Neustoichivosti gazovogo grav... | Oglavlenie | 4.5 Gidrodinamicheskie neustoichivosti ... >>

Publikacii s klyuchevymi slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Sm. takzhe: Akkrecionnyi disk chernoi dyry: vizualizaciya Dvazhdy iskrivlennyi mir dvoinyh chernyh dyr Spiral'nyi disk vokrug chernoi dyry V centre spiral'noi galaktiki NGC 3521 Massivnaya chernaya dyra razryvaet proletayushuyu zvezdu Ul'trafioletovye kol'ca M31 Blizkaya massivnaya spiral'naya galaktika NGC 2841 Vse publikacii na tu zhe temu >>