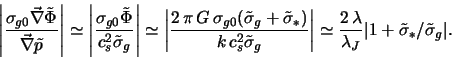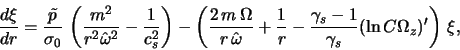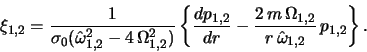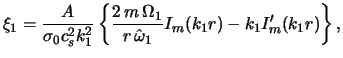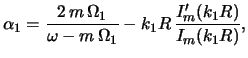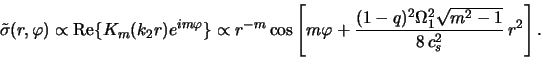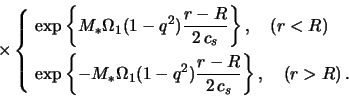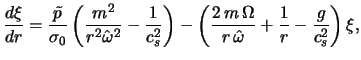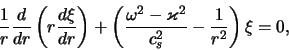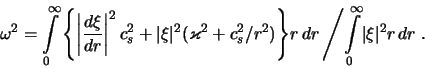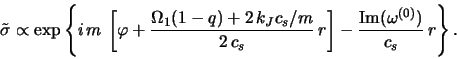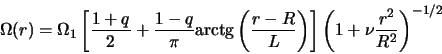<< 4.4 Dissipativnye effekty | Oglavlenie | 4.6 Neosesimmetrichnyi potencial >>
- 4.5.1 Dispersionnoe uravnenie vozmushenii razryva uglovoi skorosti
- 4.5.2 Neustoichivost' Kel'vina-Gel'mgol'ca
- 4.5.3 Centrobezhnaya neustoichivost'
- 4.5.4 Neustoichivost' skachka skorosti vrasheniya konechnoi shiriny
- 4.5.5 Skachok plotnosti
- 4.5.6 Neodnorodnye gazovye diski s dvugorbymi krivymi vrasheniya
- 4.5.7 Nizkochastotnaya centrobezhnaya neustoichivost'
4.5 Gidrodinamicheskie neustoichivosti gazovogo diska
V predydushih razdelah etoi glavy my uzhe rassmotreli ryad gidrodinamicheskih neustoichivostei gazovogo gravitiruyushego diska, imeyushih, po-vidimomu, otnoshenie k proishozhdeniyu teh ili inyh nablyudaemyh struktur ili nalagayushih ogranicheniya na znacheniya nekotoryh parametrov galakticheskih gazovyh podsistem. Eto prezhde vsego gravitacionnaya (ili gravitacionno-gradientnaya) neustoichivost', opredelyayushaya minimal'nuyu "temperaturu" diska, neobhodimuyu dlya predotvrasheniya razbieniya ego na gravitacionno svyazannye sgustki dzhinsovskogo masshtaba. Drugoi klass neustoichivostei, obuslovlennyh radial'noi neodnorodnost'yu plotnosti i temperatury diska, vliyaet na otnoshenie radial'nyh gradientov ukazannyh velichin i, vozmozhno, mozhet privodit' k vozbuzhdeniyu anticiklonicheskih vihrevyh struktur tipa solitonov Rossbi. Bystraya dissipativnaya neustoichivost' mozhet igrat' rol' v reshenii problemy turbulentnoi vyazkosti.
Odnako sredi perechislennyh vyshe neustoichivostei net
neustoichivosti, obuslovlennoi neposredstvenno differencial'nost'yu
vrasheniya diska. Neustoichivosti takogo tipa mogut vozbuzhdat'sya v
teh chastyah diska, gde stepen' differencial'nosti vrasheniya veshestva
prevyshaet nekotoryi predel -- naprimer, v oblasti rezkogo ubyvaniya
![]() snaruzhi ot vnutrennego gorba
snaruzhi ot vnutrennego gorba
![]() v galaktikah
s dvugorbymi krivymi vrasheniya (sm. ris. 1.1).
v galaktikah
s dvugorbymi krivymi vrasheniya (sm. ris. 1.1).
Po krainei mere v nashei Galaktike v etoi zhe oblasti (
![]() kpk) nablyudaetsya zametnaya depressiya v poverhnostnoi plotnosti
gazovogo diska. Pryamaya ocenka po dannym nablyudenii [70]
dzhinsovskogo masshtaba v etoi chasti gazovoi podsistemy Galaktiki
privodit k sleduyushemu rezul'tatu:
kpk) nablyudaetsya zametnaya depressiya v poverhnostnoi plotnosti
gazovogo diska. Pryamaya ocenka po dannym nablyudenii [70]
dzhinsovskogo masshtaba v etoi chasti gazovoi podsistemy Galaktiki
privodit k sleduyushemu rezul'tatu:
![]() kpk, chto bol'she masshtabov nablyudaemyh
struktur. Kakovy zhe sledstviya etogo rezul'tata?
kpk, chto bol'she masshtabov nablyudaemyh
struktur. Kakovy zhe sledstviya etogo rezul'tata?
Dinamika vozmushenii v gazovom diske opredelyaetsya summoi dvuh
sil:
![]() , gde
, gde
![]() ,
, ![]() -- vozmushennye davlenie i
gravitacionnyi potencial. Ocenim ih otnositel'nuyu intensivnost'
-- vozmushennye davlenie i
gravitacionnyi potencial. Ocenim ih otnositel'nuyu intensivnost'
Ocenki, provedennye v sootvetstvii s rezul'tatami p. 4.1.2 po
dannym nablyudenii ravnovesnyh parametrov zvezdnoi i gazovoi
ploskih podsistem v rassmatrivaemoi oblasti Galaktiki, pokazyvayut,
chto vklad zvezdnogo diska v vozmushennyi gravitacionnyi potencial
ne prevyshaet vklad gazovogo (sm. razd. 6.2). Poetomu esli kakaya-libo gidrodinamicheskaya neustoichivost' privodit k raskachke
vozmushenii s
![]() , to v uravneniyah, opisyvayushih dinamiku
gazovogo diska, vozmushennoi gravitacionnoi siloi (
, to v uravneniyah, opisyvayushih dinamiku
gazovogo diska, vozmushennoi gravitacionnoi siloi (
![]() )
v pervom priblizhenii mozhno prenebrech' po sravneniyu s vozmushennoi
gidrodinamicheskoi siloi (
)
v pervom priblizhenii mozhno prenebrech' po sravneniyu s vozmushennoi
gidrodinamicheskoi siloi (
![]() ). Etot vyvod poluchil
obosnovannoe podtverzhdenie v podrobno opisannyh Fridmanom i Polyachenko
[2] rabotah [345-348]. Poetomu dalee v etom razdele (krome
p. 4.5.4) my ne budem uchityvat' vklad vozmushennogo gravitacionnogo
potenciala v dinamiku vozmushenii gazovogo diska. Podpobnoe obsuzhdenie
etogo vopposa mozhno naiti v pabote [349].
). Etot vyvod poluchil
obosnovannoe podtverzhdenie v podrobno opisannyh Fridmanom i Polyachenko
[2] rabotah [345-348]. Poetomu dalee v etom razdele (krome
p. 4.5.4) my ne budem uchityvat' vklad vozmushennogo gravitacionnogo
potenciala v dinamiku vozmushenii gazovogo diska. Podpobnoe obsuzhdenie
etogo vopposa mozhno naiti v pabote [349].
4.5.1 Dispersionnoe uravnenie vozmushenii razryva uglovoi skorosti
Issleduem dinamiku vozmushenii v odnorodnom gazovom diske,
vrashayushemsya s razryvom uglovoi skorosti [predel'naya model'
dvugorboi krivoi vrasheniya s uzkoi oblast'yu rezkogo ubyvaniya ![]() snaruzhi ot vnutrennego gorba
snaruzhi ot vnutrennego gorba
![]() ]:
]:
pri
V ramkah modeli s nepreryvnym raspredeleniem ![]() iz
linearizovannyh uravnenii gazodinamiki (4.2.14)
iz
linearizovannyh uravnenii gazodinamiki (4.2.14) ![]() (4.2.17) dlya
vozmushenii tipa (4.2.13) s uchetom nesushestvennosti vozmushenii
gravitacionnogo potenciala poluchaem sistemu uravnenii
(4.2.17) dlya
vozmushenii tipa (4.2.13) s uchetom nesushestvennosti vozmushenii
gravitacionnogo potenciala poluchaem sistemu uravnenii
gde
Perehodya k modeli razryva ![]() (4.5.2), budem iskat' resheniya
sistemy (4.5.4), (4.5.5) otdel'no po obe storony ot razryva (
(4.5.2), budem iskat' resheniya
sistemy (4.5.4), (4.5.5) otdel'no po obe storony ot razryva (![]() ,
, ![]() ), polagaya sootvetstvenno
), polagaya sootvetstvenno
![]() . Pri
etom sistema uravnenii (4.5.4), (4.5.5) svoditsya k odnomu dlya
. Pri
etom sistema uravnenii (4.5.4), (4.5.5) svoditsya k odnomu dlya
![]() :
:
Resheniya etih uravnenii dolzhny byt' sshity na razryve (pri
Vtoroe iz etih granichnyh uslovii vyglyadit
neobychnym4.5. Poyasnim poetomu ego fizicheskuyu sushnost'. Radial'noe
ravnovesie gazovyh galakticheskih diskov obuslovleno balansom gradienta
davleniya, centrobezhnoi i gravitacionnoi sil:
![]() , gde shtrih oznachaet differencirovanie po radial'noi koordinate.
Vklad gradienta davleniya v eto uslovie mal po sravneniyu s vkladom
gravitacionnoi sily
, gde shtrih oznachaet differencirovanie po radial'noi koordinate.
Vklad gradienta davleniya v eto uslovie mal po sravneniyu s vkladom
gravitacionnoi sily
![]() . Poetomu dovol'no rezkii perepad
. Poetomu dovol'no rezkii perepad ![]() v rassmatrivaemoi
nami oblasti diska obuslovlen v osnovnom v toi zhe mere rezkim
gradientom
v rassmatrivaemoi
nami oblasti diska obuslovlen v osnovnom v toi zhe mere rezkim
gradientom ![]() , sozdavaemym raspredeleniem veshestva v massivnoi
zvezdnoi podsisteme. I v predel'no idealizirovannoi modeli razryva
, sozdavaemym raspredeleniem veshestva v massivnoi
zvezdnoi podsisteme. I v predel'no idealizirovannoi modeli razryva
![]() velichina
velichina ![]() dolzhna byt', ochevidno, razryvnoi. V to zhe
vremya polnoe sovokupnoe "davlenie"
dolzhna byt', ochevidno, razryvnoi. V to zhe
vremya polnoe sovokupnoe "davlenie"
![]() dolzhno byt'
nepreryvnym na iskrivlennoi blagodarya vozmusheniyam
dolzhno byt'
nepreryvnym na iskrivlennoi blagodarya vozmusheniyam ![]() poverhnosti
razryva, a ravnovesnoe
poverhnosti
razryva, a ravnovesnoe
![]() -- nepreryvnym na
nevozmushennom razryve. Razlozhim etu velichinu v ryad po stepenyam amplitudy
vozmushenii, ogranichivayas' lineinymi chlenami i prenebregaya v sootvetstvii s
ocenkoi (4.5.1) vozmushennym gravitacionnym potencialom:
-- nepreryvnym na
nevozmushennom razryve. Razlozhim etu velichinu v ryad po stepenyam amplitudy
vozmushenii, ogranichivayas' lineinymi chlenami i prenebregaya v sootvetstvii s
ocenkoi (4.5.1) vozmushennym gravitacionnym potencialom:
otkuda sleduet, chto nepreryvnoi na razryve
Resheniya uravnenii (4.5.6), (4.5.7) dolzhny byt' ogranicheny pri
![]() i
i
![]() . S uchetom etih granichnyh
uslovii oni imeyut vid
. S uchetom etih granichnyh
uslovii oni imeyut vid
gde
Sshivaya zatem resheniya (4.5.10)-(4.5.13) na razryve ![]() soglasno granichnym usloviyam (4.5.8), (4.5.9), poluchaem iskomoe
dispersionnoe uravnenie [351]:
soglasno granichnym usloviyam (4.5.8), (4.5.9), poluchaem iskomoe
dispersionnoe uravnenie [351]:
Dlya naglyadnosti predstavleniya rezul'tatov budem opisyvat'
resheniya dispersionnogo uravneniya (4.5.15) s pomosh'yu dvuh
bezrazmernyh parametrov
![]() i
i
![]() .
.
4.5.2 Neustoichivost' Kel'vina-Gel'mgol'ca
Poluchim reshenie dispersionnogo uravneniya (4.5.15) v predele
"slabogo" (![]() ) razryva. Netrudno videt', chto v etom sluchae
soglasno (4.5.14)
) razryva. Netrudno videt', chto v etom sluchae
soglasno (4.5.14)
![]() . Poetomu, ispol'zuya
predstavleniya funkcii Besselya v vide ryadov po stepenyam ih argumentov,
iz (4.5.15) poluchaem (
. Poetomu, ispol'zuya
predstavleniya funkcii Besselya v vide ryadov po stepenyam ih argumentov,
iz (4.5.15) poluchaem (![]() )
)
gde
Poskol'ku v prenebrezhenii gradientami ravnovesnyh plotnosti i
davleniya gazovoi podsistemy vozmushennye poverhnostnye plotnost' ![]() i davlenie
i davlenie ![]() svyazany sootnosheniem
svyazany sootnosheniem
![]() ,
netrudno opredelit' prostranstvennuyu zavisimost'
,
netrudno opredelit' prostranstvennuyu zavisimost'
![]() .
Naprimer, v oblasti
.
Naprimer, v oblasti ![]() pri
pri ![]() , ispol'zuya rezul'tat
(4.5.18) i sootnoshenie (4.5.14), uchityvaya, chto fizicheskii smysl
imeyut deistvitel'nye chasti kompleksnyh amplitud, poluchaem
, ispol'zuya rezul'tat
(4.5.18) i sootnoshenie (4.5.14), uchityvaya, chto fizicheskii smysl
imeyut deistvitel'nye chasti kompleksnyh amplitud, poluchaem
4.5.3 Centrobezhnaya neustoichivost'
V spiral'nyh galaktikah, kak pravilo, znachenie
![]() na
vnutrennem gorbe krivoi vrasheniya namnogo bol'she skorosti zvuka v
gazovoi podsisteme i, takim obrazom, osushestvlyaetsya drugoi
predel'nyi sluchai:
na
vnutrennem gorbe krivoi vrasheniya namnogo bol'she skorosti zvuka v
gazovoi podsisteme i, takim obrazom, osushestvlyaetsya drugoi
predel'nyi sluchai: ![]() . V etom predele, ispol'zuya
asimptoticheskie predstavleniya funkcii Besselya pri
. V etom predele, ispol'zuya
asimptoticheskie predstavleniya funkcii Besselya pri
![]() , iz (4.5.15) v glavnom poryadke ukazannyh asimptotik poluchaem [351]
, iz (4.5.15) v glavnom poryadke ukazannyh asimptotik poluchaem [351]
V rassmotrennom predele (![]() ) neustoichivost' (4.5.21) uzhe
ne pohozha na neustoichivost' tangencial'nogo razryva (4.5.18). Vo-pervyh, potomu, chto ona razvivaetsya tol'ko v tom sluchae, kogda
vnutrennyaya chast' diska vrashaetsya bystree vneshnei:
) neustoichivost' (4.5.21) uzhe
ne pohozha na neustoichivost' tangencial'nogo razryva (4.5.18). Vo-pervyh, potomu, chto ona razvivaetsya tol'ko v tom sluchae, kogda
vnutrennyaya chast' diska vrashaetsya bystree vneshnei: ![]() . Vo-vtoryh, potomu, chto ee inkrement prakticheski ne zavisit ot
volnovogo chisla
. Vo-vtoryh, potomu, chto ee inkrement prakticheski ne zavisit ot
volnovogo chisla
![]() [sr. s (4.5.18)]4.6. V-tret'ih, potomu, chto neustoichivost' (4.5.21) v
protivopolozhnost' klassicheskoi neustoichivosti tangencial'nogo razryva
ne stabiliziruetsya pri
[sr. s (4.5.18)]4.6. V-tret'ih, potomu, chto neustoichivost' (4.5.21) v
protivopolozhnost' klassicheskoi neustoichivosti tangencial'nogo razryva
ne stabiliziruetsya pri
![]() ,
a imeet mesto pri skol' ugodno bol'shom
,
a imeet mesto pri skol' ugodno bol'shom
![]() i bolee
togo, inkrement neustoichivosti (4.5.21) rastet prakticheski lineino s
rostom
i bolee
togo, inkrement neustoichivosti (4.5.21) rastet prakticheski lineino s
rostom ![]() [o stabilizacii klassicheskoi neustoichivosti tangencial'nogo
razryva v dvumernoi gazodinamike sm. v knige Landau i Lifshica [327];
etot effekt legko poluchit' iz formuly (5.3.18)].
[o stabilizacii klassicheskoi neustoichivosti tangencial'nogo
razryva v dvumernoi gazodinamike sm. v knige Landau i Lifshica [327];
etot effekt legko poluchit' iz formuly (5.3.18)].
Dlya vyyasneniya prirody neustoichivosti (4.5.21) rassmotrim
dinamiku vozmusheniya granicy razryva, imeyushego, naprimer, formu
vystupa v oblast' ![]() . Veshestvo, soderzhasheesya v etom vystupe,
prodolzhaet vrashat'sya s uglovoi skorost'yu
. Veshestvo, soderzhasheesya v etom vystupe,
prodolzhaet vrashat'sya s uglovoi skorost'yu ![]() i na nego deistvuet
(prihodyashaya na edinicu massy) centrobezhnaya sila
i na nego deistvuet
(prihodyashaya na edinicu massy) centrobezhnaya sila
![]() . No etot vystup uzhe nahoditsya v oblasti, gde soglasno usloviyu
radial'nogo ravnovesiya gravitacionnaya sila
. No etot vystup uzhe nahoditsya v oblasti, gde soglasno usloviyu
radial'nogo ravnovesiya gravitacionnaya sila
![]() (pri
(pri
![]() ).
Voznikayushaya pri etom napravlennaya naruzhu sila
).
Voznikayushaya pri etom napravlennaya naruzhu sila
![]() uvelichivaet amplitudu vystupa
i tem samym privodit k neustoichivosti. V sluchae
uvelichivaet amplitudu vystupa
i tem samym privodit k neustoichivosti. V sluchae
![]() voznikayushaya sila napravlena k centru diska i, sledovatel'no,
stremitsya umen'shit' amplitudu vystupa -- eto ob'yasnyaet prichinu ustoichivosti
v sluchae
voznikayushaya sila napravlena k centru diska i, sledovatel'no,
stremitsya umen'shit' amplitudu vystupa -- eto ob'yasnyaet prichinu ustoichivosti
v sluchae ![]() (
(
![]() ). Privedennye vyshe dovody korrektny,
esli vklad davleniya v uslovie radial'nogo ravnovesiya gazovogo diska
prenebrezhimo mal, a eto mozhet imet' mesto lish' v tom sluchae, kogda
). Privedennye vyshe dovody korrektny,
esli vklad davleniya v uslovie radial'nogo ravnovesiya gazovogo diska
prenebrezhimo mal, a eto mozhet imet' mesto lish' v tom sluchae, kogda
![]() (
(![]() ). Analogichnye rassuzhdeniya v sluchae
vozmusheniya granicy razryva
). Analogichnye rassuzhdeniya v sluchae
vozmusheniya granicy razryva ![]() , imeyushei formu "vmyatiny" v oblast'
, imeyushei formu "vmyatiny" v oblast'
![]() , takzhe privodyat k vyvodu o neustoichivosti tol'ko pri
, takzhe privodyat k vyvodu o neustoichivosti tol'ko pri
![]() (
(![]() ). Poetomu ne yavlyaetsya
udivitel'nym tot fakt, chto inkrement neustoichivosti (4.5.21)
proporcionalen razryvu deistvuyushei na edinicu massy centrobezhnoi
sily. V svyazi s etim neustoichivost' (4.5.21) estestvenno nazyvat'
centrobezhnoi.
). Poetomu ne yavlyaetsya
udivitel'nym tot fakt, chto inkrement neustoichivosti (4.5.21)
proporcionalen razryvu deistvuyushei na edinicu massy centrobezhnoi
sily. V svyazi s etim neustoichivost' (4.5.21) estestvenno nazyvat'
centrobezhnoi.
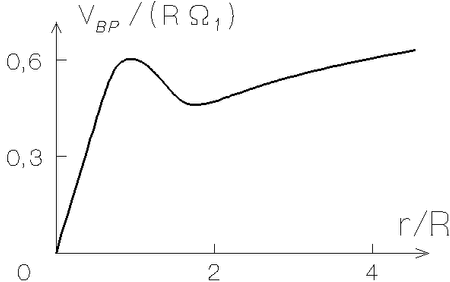
 |
Ris. 4.8. Zavisimost' inkrementa neustoichivosti,
opisyvaemoi dispersionnym uravneniem (4.5.15), ot parametra
|
Razlichie mezhdu neustoichivostyami Kel'vina-Gel'mgol'ca [NKG --
(4.5.18)] i centrobezhnoi [CBN -- (4.5.21)] horosho vidno na ris. 4.8,
gde izobrazhena zavisimost' inkrementa neustoichivosti, opisyvaemoi
dispersionnym uravneniem (4.5.15) pri znacheniyah parametra
![]() i
i ![]() dlya mody
dlya mody ![]() . Vidno,
chto pri
. Vidno,
chto pri ![]() inkrementy v oboih sluchayah (
inkrementy v oboih sluchayah (![]() ;
;
![]() ) blizki drug k drugu, no pri
) blizki drug k drugu, no pri
![]() ih
razlichie okazyvaetsya ves'ma sushestvennym: pri
ih
razlichie okazyvaetsya ves'ma sushestvennym: pri ![]() vozbuzhdaetsya
tol'ko NKG, a pri
vozbuzhdaetsya
tol'ko NKG, a pri ![]() osnovnoi vklad v inkrement
neustoichivosti daet mehanizm CBN.
osnovnoi vklad v inkrement
neustoichivosti daet mehanizm CBN.
Rassmotrim teper' vopros o prostranstvennoi strukture
vozmushenii plotnosti, vozbuzhdaemyh centrobezhnoi neustoichivost'yu. S
uchetom togo, chto eta neustoichivost' imeet mesto pri ![]() ,
ispol'zuem v (4.5.10), (4.5.11) asimptoticheskie predstavleniya
funkcii Besselya. V rezul'tate poluchaem
,
ispol'zuem v (4.5.10), (4.5.11) asimptoticheskie predstavleniya
funkcii Besselya. V rezul'tate poluchaem
Otsyuda vidno, chto neustoichivye po (4.5.21) vozmusheniya plotnosti imeyut formu otstayushih spiralei. Shag takoi spirali v radial'nom napravlenii opredelyaetsya sootnosheniem
a uglovaya skorost' ee vrasheniya
V to zhe vremya amplituda etih vozmushenii dovol'no bystro ubyvaet s udaleniem ot razryva -- soglasno (4.5.23) harakternyi masshtab ubyvaniya amplitudy
i pri
Summiruem poluchennye rezul'taty. Centrobezhnaya neustoichivost'
harakterizuetsya bol'shim inkrementom i vozbuzhdaemye eyu vozmusheniya
plotnosti predstavlyayut soboi otstayushie spirali. Poslednee
obstoyatel'stvo vyglyadit ves'ma zamanchivym s tochki zreniya
vozmozhnogo resheniya problemy proishozhdeniya spiral'nogo uzora
galaktik4.7. Odnako v ramkah rassmotrennoi nami idealizirovannoi
modeli razryva ![]() centrobezhnaya neustoichivost' generiruet slishkom
korotkie otrezki spiralei (
centrobezhnaya neustoichivost' generiruet slishkom
korotkie otrezki spiralei (![]() ) i ne vydelyaet po velichine
inkrementa kakuyu-libo konkretnuyu modu. V to zhe vremya yasno, chto
issledovanie bolee realistichnyh modelei s razmazannym "razryvom"
) i ne vydelyaet po velichine
inkrementa kakuyu-libo konkretnuyu modu. V to zhe vremya yasno, chto
issledovanie bolee realistichnyh modelei s razmazannym "razryvom" ![]() vydelit kak naibolee neustoichivye nizshie mody (vysshie mody s
vydelit kak naibolee neustoichivye nizshie mody (vysshie mody s
![]() , gde
, gde ![]() -- shirina razmazki "razryva"
-- shirina razmazki "razryva" ![]() , ne budut "vosprinimat'"
oblast' rezkogo izmeneniya
, ne budut "vosprinimat'"
oblast' rezkogo izmeneniya ![]() kak razryv i, sledovatel'no, ne budut
vozbuzhdat'sya). S drugoi storony, obshee umen'shenie inkrementa
neustoichivosti s rostom shiriny razmazki "razryva" dolzhno uvelichit'
radial'nuyu protyazhennost' vozbuzhdaemoi struktury [sm. (4.5.26)].
Poetomu podrobnoe issledovanie centrobezhnoi neustoichivosti na
bolee realistichnyh modelyah predstavlyaetsya ves'ma aktual'nym.
kak razryv i, sledovatel'no, ne budut
vozbuzhdat'sya). S drugoi storony, obshee umen'shenie inkrementa
neustoichivosti s rostom shiriny razmazki "razryva" dolzhno uvelichit'
radial'nuyu protyazhennost' vozbuzhdaemoi struktury [sm. (4.5.26)].
Poetomu podrobnoe issledovanie centrobezhnoi neustoichivosti na
bolee realistichnyh modelyah predstavlyaetsya ves'ma aktual'nym.
4.5.4 Neustoichivost' skachka skorosti vrasheniya konechnoi shiriny
Opredelim vliyanie "razmazki" razryva uglovoi skorosti ![]() na
poluchennye vyshe rezul'taty. V pervom priblizhenii polagaem, chto v
oblasti
na
poluchennye vyshe rezul'taty. V pervom priblizhenii polagaem, chto v
oblasti
![]() s dostatochno malym
s dostatochno malym
![]() osushestvlyaetsya plavnyi perehod ot znacheniya
osushestvlyaetsya plavnyi perehod ot znacheniya
![]() do
do
![]() . Ispol'zuem takzhe tot fakt,
chto v naibolee interesnom dlya nas sluchae
. Ispol'zuem takzhe tot fakt,
chto v naibolee interesnom dlya nas sluchae ![]() struktura
neustoichivyh vozmushenii v radial'nom napravlenii yavlyaetsya korotkovolnovoi
[
struktura
neustoichivyh vozmushenii v radial'nom napravlenii yavlyaetsya korotkovolnovoi
[
![]() ,
,
![]() ]. Dlya lineinoi
approksimacii
]. Dlya lineinoi
approksimacii ![]() v perehodnoi oblasti v glavnom poryadke po maloi
velichine
v perehodnoi oblasti v glavnom poryadke po maloi
velichine
gde
Otsyuda vidno, chto v priblizhenii (4.5.27) velichina
![]() ,
opredelyayushaya stepen' zakrutki spiralei [sm. (4.5.24)], ne
izmenyaetsya. Odnako inkrement neustoichivosti
,
opredelyayushaya stepen' zakrutki spiralei [sm. (4.5.24)], ne
izmenyaetsya. Odnako inkrement neustoichivosti
![]() umen'shaetsya
dovol'no rezko. Eto privodit k dvum vazhnym sledstviyam. Vo-pervyh,
vozmusheniya s malym chislom spiralei okazyvayutsya bolee
neustoichivymi, chem vozmusheniya s
umen'shaetsya
dovol'no rezko. Eto privodit k dvum vazhnym sledstviyam. Vo-pervyh,
vozmusheniya s malym chislom spiralei okazyvayutsya bolee
neustoichivymi, chem vozmusheniya s ![]() . Vo-vtoryh, obshee (i
osnovnoe iz-za
. Vo-vtoryh, obshee (i
osnovnoe iz-za ![]() ) umen'shenie inkrementa v sootvetstvii s
(4.5.26) uvelichivaet harakternyi masshtab
) umen'shenie inkrementa v sootvetstvii s
(4.5.26) uvelichivaet harakternyi masshtab ![]() ubyvaniya amplitudy vozmushenii v radial'nom napravlenii, chto
rasshiryaet oblast' lokalizacii generiruemogo spiral'nogo uzora.
ubyvaniya amplitudy vozmushenii v radial'nom napravlenii, chto
rasshiryaet oblast' lokalizacii generiruemogo spiral'nogo uzora.
V real'nyh spiral'nyh galaktikah s dvugorbymi krivymi
vrasheniya "razmazka" razryva ![]() zametno bol'she, chem dopuskaet
uslovie (4.5.27). Poetomu, rassmatrivaya poluchennye vyshe rezul'taty
v modeli so slaboi "razmazkoi" s tochki zreniya opredeleniya
tendencii v izmenenii
zametno bol'she, chem dopuskaet
uslovie (4.5.27). Poetomu, rassmatrivaya poluchennye vyshe rezul'taty
v modeli so slaboi "razmazkoi" s tochki zreniya opredeleniya
tendencii v izmenenii
![]() , sleduet vse zhe vychislyat' poslednyuyu
[kak i
, sleduet vse zhe vychislyat' poslednyuyu
[kak i
![]() ] na modelyah s krivymi vrasheniya, blizkimi k real'nym.
V kachestve takoi modeli ispol'zuem krivuyu vrasheniya (4.5.3),
obladayushuyu tem svoistvom, chto v predele
] na modelyah s krivymi vrasheniya, blizkimi k real'nym.
V kachestve takoi modeli ispol'zuem krivuyu vrasheniya (4.5.3),
obladayushuyu tem svoistvom, chto v predele
![]() eta funkciya
perehodit v issledovannyi vyshe razryv
eta funkciya
perehodit v issledovannyi vyshe razryv ![]() . S takoi krivoi vrasheniya
sistemu uravnenii (4.5.4), (4.5.5) mozhno reshat' chislenno na EVM
kak zadachu tipa Shturma-Liuvillya (opredelyat' sobstvennye funkcii
. S takoi krivoi vrasheniya
sistemu uravnenii (4.5.4), (4.5.5) mozhno reshat' chislenno na EVM
kak zadachu tipa Shturma-Liuvillya (opredelyat' sobstvennye funkcii ![]() ,
, ![]() i sobstvennye znacheniya
i sobstvennye znacheniya ![]() ) pri granichnyh usloviyah
) pri granichnyh usloviyah
Yasno, chto, polagaya radial'noe smeshenie
Opishem kratko rezul'taty v naibolee interesnoi s tochki zreniya
prilozhenii oblasti parametrov
![]() ;
;
![]() [353,354,356].
[353,354,356].
- Vysshie mody (
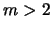 ) stabiliziruyutsya polnost'yu pri
) stabiliziruyutsya polnost'yu pri
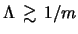 . Moda
. Moda 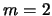 stabiliziruetsya pri
stabiliziruetsya pri
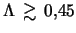 (v predele
(v predele
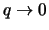 ). Etot rezul'tat netrudno ponyat': vo vrashayusheisya
neszhimaemoi zhidkosti dlya raskachki vozmushenii s
). Etot rezul'tat netrudno ponyat': vo vrashayusheisya
neszhimaemoi zhidkosti dlya raskachki vozmushenii s 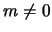 neobhodimo, chtoby
zavihrennost'
neobhodimo, chtoby
zavihrennost'
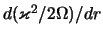 izmenyala znak pri konechnom
izmenyala znak pri konechnom
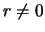 [357]. Dlya
[357]. Dlya 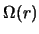 (4.5.3) tochki izmeneniya znaka upomyanutoi
velichiny sushestvuyut pri
(4.5.3) tochki izmeneniya znaka upomyanutoi
velichiny sushestvuyut pri
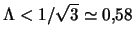 . Otklonenie
granicy ustoichivosti v nashem sluchae v men'shuyu storonu po parametru
. Otklonenie
granicy ustoichivosti v nashem sluchae v men'shuyu storonu po parametru
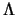 obuslovleno, po-vidimomu, stabiliziruyushim vliyaniem szhimaemosti
sredy.
obuslovleno, po-vidimomu, stabiliziruyushim vliyaniem szhimaemosti
sredy.
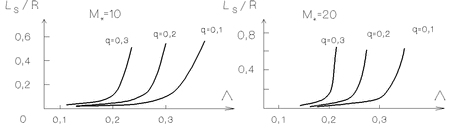
Ris. 4.9. Oblasti dominirovaniya razlichnyh mod (
 ) po
inkrementu v ploskosti
parametrov
) po
inkrementu v ploskosti
parametrov
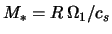 ;
;
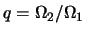 : a -- pri
: a -- pri
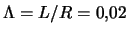 ; b -- pri
; b -- pri
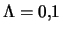 . Chisla
v granichnyh tochkah krivyh --
inkrementy v edinicah
. Chisla
v granichnyh tochkah krivyh --
inkrementy v edinicah 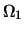 .
. - V oblasti parametrov
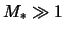 ,
, 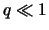 naibolee
neustoichivymi (bez ucheta mod
naibolee
neustoichivymi (bez ucheta mod 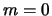 i
i 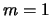 -- ob etom sm. nizhe)
okazyvayutsya dvuhrukavnye (
-- ob etom sm. nizhe)
okazyvayutsya dvuhrukavnye (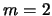 ) vozmusheniya. Etot rezul'tat
illyustriruet ris. 4.9, gde v ploskosti parametrov
) vozmusheniya. Etot rezul'tat
illyustriruet ris. 4.9, gde v ploskosti parametrov 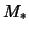 ,
, 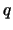 izobrazheny
oblasti dominirovaniya po inkrementu mod
izobrazheny
oblasti dominirovaniya po inkrementu mod 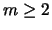 pri
pri
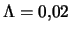 i
i
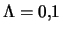 . Vidno, chto s rostom parametra
. Vidno, chto s rostom parametra 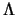 oblast'
dominirovaniya mody
oblast'
dominirovaniya mody 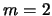 bystro rasshiryaetsya.
bystro rasshiryaetsya.
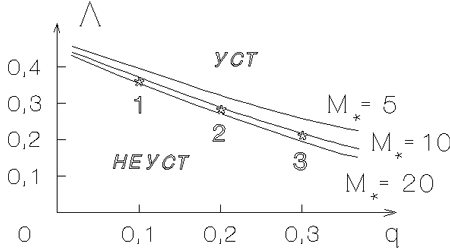
Ris. 4.10. Krivye marginal'noi ustoichivosti mody
 , kazhdaya tochka
kotoryh [para znachenii
(
, kazhdaya tochka
kotoryh [para znachenii
( )] opredelyaet profil'
krivoi vrasheniya (4.5.3),
dlya kotorogo
)] opredelyaet profil'
krivoi vrasheniya (4.5.3),
dlya kotorogo
 pri
sootvetstvuyushem znachenii
parametra
pri
sootvetstvuyushem znachenii
parametra 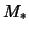 . Profili
. Profili
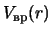 , sootvetstvuyushie
tochkam
, sootvetstvuyushie
tochkam  --
--  , -- sm. ris. 4.11.
, -- sm. ris. 4.11.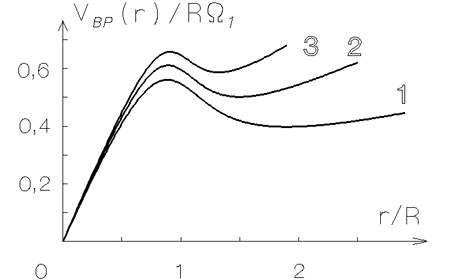
Ris. 4.11. Krivye vrasheniya (okrestnost' vnutrennego gorba), dopuskayushie vozbuzhdenie dvuhrukavnogo spiral'nogo uzora s malym inkrementom (sm. ris. 4.10) pri
 . Sovokupnost' parametrov
. Sovokupnost' parametrov

 dlya
etih krivyh imeet sleduyushie znacheniya:
1 --
dlya
etih krivyh imeet sleduyushie znacheniya:
1 --
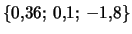 ;
2 --
;
2 --
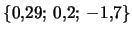 ;
3 --
;
3 --
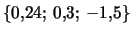 .
.
- Dlya dvuhrukavnyh vozmushenii oblast' neustoichivosti v
ploskosti parametrov
 ,
, 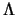 dovol'no velika (ris. 4.10) i ee razmery
slabo zavisyat ot velichiny
dovol'no velika (ris. 4.10) i ee razmery
slabo zavisyat ot velichiny 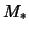 pri
pri 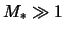 . Na ris. 4.11 dlya primera
privedeny tri krivye vrasheniya (4.5.3) (v okrestnosti vnutrennego
gorba), harakterizuemye parametrami, obespechivayushimi vozbuzhdenie
dvuhrukavnoi spirali v modeli s
. Na ris. 4.11 dlya primera
privedeny tri krivye vrasheniya (4.5.3) (v okrestnosti vnutrennego
gorba), harakterizuemye parametrami, obespechivayushimi vozbuzhdenie
dvuhrukavnoi spirali v modeli s 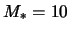 s malym inkrementom. Vidno,
chto dlya vozbuzhdeniya spiral'nogo uzora s pomosh'yu izuchaemogo nami
mehanizma ploskoi galaktike dostatochno obladat' krivoi vrasheniya
dazhe so slabo vyrazhennoi dvugorbost'yu. Takie krivye vrasheniya
rasprostraneny dovol'no shiroko [29-31,45-48].
s malym inkrementom. Vidno,
chto dlya vozbuzhdeniya spiral'nogo uzora s pomosh'yu izuchaemogo nami
mehanizma ploskoi galaktike dostatochno obladat' krivoi vrasheniya
dazhe so slabo vyrazhennoi dvugorbost'yu. Takie krivye vrasheniya
rasprostraneny dovol'no shiroko [29-31,45-48].
- S rostom parametra
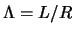 proishodit nekotoroe umen'shenie
proishodit nekotoroe umen'shenie
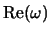 . Pri dostatochno malom
. Pri dostatochno malom
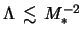 [sm. uslovie (4.5.27)] otlichie
[sm. uslovie (4.5.27)] otlichie
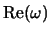 ot znachenii (4.5.21)
ne prevyshaet 1% v sootvetstvii s rezul'tatom (4.5.28). No pri konechnyh
ot znachenii (4.5.21)
ne prevyshaet 1% v sootvetstvii s rezul'tatom (4.5.28). No pri konechnyh
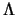 etot effekt stanovitsya zametnym4.8i privodit k sootvetstvuyushim rostu shaga spirali [sm.(4.5.21)] i umen'sheniyu
uglovoi skorosti ee vrasheniya
etot effekt stanovitsya zametnym4.8i privodit k sootvetstvuyushim rostu shaga spirali [sm.(4.5.21)] i umen'sheniyu
uglovoi skorosti ee vrasheniya
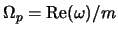 [sm.(4.5.25)].
[sm.(4.5.25)].
- Vo vsei issledovannoi oblasti parametrov
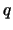 ,
, 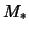 ,
, 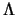 harakternyi masshtab ubyvaniya amplitudy vozmushennoi plotnosti
harakternyi masshtab ubyvaniya amplitudy vozmushennoi plotnosti 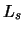 s
udaleniem ot "razryva" v oblast'
s
udaleniem ot "razryva" v oblast'  udovletvoritel'no
opisyvaetsya sootnosheniem [sr. s (4.5.26)]
udovletvoritel'no
opisyvaetsya sootnosheniem [sr. s (4.5.26)]
 |
Ris. 4.12. Zavisimost' masshtaba radial'nogo ubyvaniya amplitudy
vozmushennoi plotnosti |
Takim obrazom, sushestvennoe umen'shenie inkrementa neustoichivosti s
rostom parametra ![]() privodit k ves'ma zametnomu rasshireniyu oblasti
lokalizacii generiruemogo spiral'nogo uzora. Etot effekt
illyustriruet ris. 4.12 [zavisimost'
privodit k ves'ma zametnomu rasshireniyu oblasti
lokalizacii generiruemogo spiral'nogo uzora. Etot effekt
illyustriruet ris. 4.12 [zavisimost' ![]() ] i ris. 4.13, na kotorom
izobrazheny primery sobstvennyh funkcii vozmushennoi plotnosti
] i ris. 4.13, na kotorom
izobrazheny primery sobstvennyh funkcii vozmushennoi plotnosti
![]() .
.
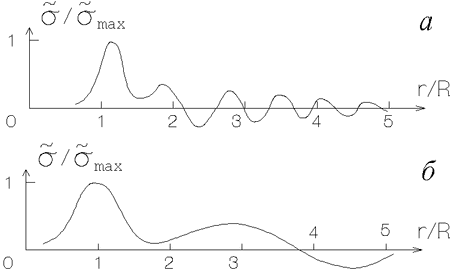 |
Ris. 4.13. Vozmushennaya
poverhnostnaya
plotnost'
|
Vazhnym takzhe yavlyaetsya vopros o zavisimosti privedennyh vyshe
rezul'tatov ot haraktera krivoi vrasheniya za predelami zony
"razmazki" razryva ![]() . Deistvitel'no, real'nye krivye vrasheniya
galaktik v oblasti
. Deistvitel'no, real'nye krivye vrasheniya
galaktik v oblasti ![]() obychno harakterizuyutsya zakonom vrasheniya
obychno harakterizuyutsya zakonom vrasheniya
![]() s
s ![]() , chto sushestvenno otlichaetsya ot zakona
vrasheniya (4.5.3):
, chto sushestvenno otlichaetsya ot zakona
vrasheniya (4.5.3):
![]() const pri
const pri ![]() . Da i
v oblasti
. Da i
v oblasti ![]() vrashenie real'nyh galaktik zametno otlichaetsya ot
tverdotel'nogo. S cel'yu vyyasneniya vliyaniya etih faktorov byl proveden
sravnitel'nyi raschet ustoichivosti vrasheniya gaza v galaktike M81 i v
model'noi galaktike s zakonom vrasheniya (4.5.3) s prakticheski sovpadayushimi
uchastkami
vrashenie real'nyh galaktik zametno otlichaetsya ot
tverdotel'nogo. S cel'yu vyyasneniya vliyaniya etih faktorov byl proveden
sravnitel'nyi raschet ustoichivosti vrasheniya gaza v galaktike M81 i v
model'noi galaktike s zakonom vrasheniya (4.5.3) s prakticheski sovpadayushimi
uchastkami
![]() mezhdu vnutrennim gorbom i sleduyushim za nim
minimumom
mezhdu vnutrennim gorbom i sleduyushim za nim
minimumom
![]() . Nablyudaemye chasti krivoi vrasheniya v oblastyah
. Nablyudaemye chasti krivoi vrasheniya v oblastyah ![]() kpk [41] i
kpk [41] i ![]() kpk [73] byli sshity polinomom tret'ei
stepeni v oblasti
kpk [73] byli sshity polinomom tret'ei
stepeni v oblasti
![]() . Raspredelenie
. Raspredelenie
![]() takzhe bralos' iz nablyudenii [73], a
takzhe bralos' iz nablyudenii [73], a ![]() polagalas' monotonno
ubyvayushei ot
polagalas' monotonno
ubyvayushei ot
![]() km/s do
km/s do
![]() km/s.
Vychisleniya byli provedeny dlya mody
km/s.
Vychisleniya byli provedeny dlya mody ![]() na osnove uravnenii, uchityvayushih
neodnorodnost'
na osnove uravnenii, uchityvayushih
neodnorodnost' ![]() i
i ![]() [sr. s (4.5.4),(4.5.5)]:
[sr. s (4.5.4),(4.5.5)]:
gde
Rassmotrim teper' vopros o vozbuzhdenii mod ![]() i
i ![]() .
Isklyuchim iz (4.5.4), (4.5.5) vozmushennoe davlenie, v rezul'tate dlya
.
Isklyuchim iz (4.5.4), (4.5.5) vozmushennoe davlenie, v rezul'tate dlya
![]() poluchim
poluchim
Otsyuda vidno, chto neustoichivost' mody ![]() (
(![]() ) mozhet
imet' mesto tol'ko v tom sluchae, esli sushestvuet interval
) mozhet
imet' mesto tol'ko v tom sluchae, esli sushestvuet interval
![]() , vnutri kotorogo (
, vnutri kotorogo (![]() ) velichina
) velichina
![]() otricatel'na. Poslednee mozhet imet' mesto, esli
otricatel'na. Poslednee mozhet imet' mesto, esli
Dlya bol'shinstva galaktik s dvugorbymi krivymi vrasheniya ![]() i moda
i moda ![]() v nih vozbuzhdat'sya ne mozhet (v Galaktike
v nih vozbuzhdat'sya ne mozhet (v Galaktike
![]() po krivym vrasheniya Hauda [35] i Klemensa [358]).
V to zhe vremya moda
po krivym vrasheniya Hauda [35] i Klemensa [358]).
V to zhe vremya moda ![]() neustoichiva i pri
neustoichiva i pri ![]() , chto pokazali
raschety [352,353,356] (sm. ris. 4.11).
, chto pokazali
raschety [352,353,356] (sm. ris. 4.11).
Issleduya osesimmetrichnyi mehanizm vozbuzhdeniya spiralei v
izolirovannoi galaktike, my dolzhny isklyuchit' iz rassmotreniya modu
![]() , poskol'ku raskachka takih vozmushenii sdvigaet centr mass
gazovoi podsistemy otnositel'no centra mass zvezdnoi [
, poskol'ku raskachka takih vozmushenii sdvigaet centr mass
gazovoi podsistemy otnositel'no centra mass zvezdnoi [
![]() ].
Poslednee vozmozhno, po-vidimomu, tol'ko pri nalichii vneshnih
vozdeistvii na rassmatrivaemuyu sistemu.
].
Poslednee vozmozhno, po-vidimomu, tol'ko pri nalichii vneshnih
vozdeistvii na rassmatrivaemuyu sistemu.
V zaklyuchenie rassmotrim vopros o vliyanii vozmushenii
gravitacionnogo potenciala na parametry generiruemoi spiral'noi
struktury s uchetom privedennoi vo vvedenii k dannomu razdelu
ocenki: ![]() . Dlya etogo v ramkah rassmotrennoi vyshe modeli
razryva
. Dlya etogo v ramkah rassmotrennoi vyshe modeli
razryva ![]() (pri
(pri ![]() ) zamenim vozmushennoe davlenie
) zamenim vozmushennoe davlenie
![]() na
na
![]() , gde
, gde
![]() ,
a velichinu
,
a velichinu ![]() (4.5.30) na
(4.5.30) na ![]() , opredelyaemuyu iz sootnosheniya
, opredelyaemuyu iz sootnosheniya
![]()
![]() . Reshaya ispravlennoe s uchetom etoi zameny
dispersionnoe uravnenie (4.5.15) metodom vozmushenii (
. Reshaya ispravlennoe s uchetom etoi zameny
dispersionnoe uravnenie (4.5.15) metodom vozmushenii (
![]() ), nahodim [353]
), nahodim [353]
Otsyuda vidno, chto, nesmotrya na destabiliziruyushee vliyanie
(dovol'no slaboe) vozmushenii gravitacionnogo potenciala, masshtab
ubyvaniya amplitudy vozmushennoi plotnosti ne izmenyaetsya. Eto
svyazano s tem, chto naryadu s poyavleniem popravki k
![]() (4.5.37) izmenyaetsya i opredelenie
(4.5.37) izmenyaetsya i opredelenie ![]() cherez chastotu. V
rezul'tate oba effekta vzaimno kompensiruyutsya. Umen'shaetsya lish' shag
spirali [sr. s (4.5.24)]:
cherez chastotu. V
rezul'tate oba effekta vzaimno kompensiruyutsya. Umen'shaetsya lish' shag
spirali [sr. s (4.5.24)]:
4.5.5 Skachok plotnosti
(Dannyi razdel napisan sovmestno s V.V. Muscevym.)
Issleduem teper' vopros o vliyanii rezkogo izmeneniya plotnosti
gazovogo diska v okrestnosti "razryva" ![]() na parametry centrobezhnoi
neustoichivosti i vozbuzhdaemyh struktur. Prezhde vsego zametim, chto
rassmotrennye vyshe odnorodnye modeli s TR uglovoi skorosti byli
izentropicheskimi (
na parametry centrobezhnoi
neustoichivosti i vozbuzhdaemyh struktur. Prezhde vsego zametim, chto
rassmotrennye vyshe odnorodnye modeli s TR uglovoi skorosti byli
izentropicheskimi (
![]() ). Pri nalichii skachka plotnosti
neobhodimo ishodit' iz neizentropicheskih
modelei. Deistvitel'no, dlya razryvnoi modeli s (4.5.2) i
). Pri nalichii skachka plotnosti
neobhodimo ishodit' iz neizentropicheskih
modelei. Deistvitel'no, dlya razryvnoi modeli s (4.5.2) i
Zapishem usloviya sshivki dlya vozmushennyh velichin ![]() i
i ![]() ,
ishodya iz (4.5.32), (4.5.33):
,
ishodya iz (4.5.32), (4.5.33):
dlya
Nizhe ogranichimsya sluchaem
 .
Deistvuya v duhe p. 4.5.1, poluchim dispersionnoe uravnenie
.
Deistvuya v duhe p. 4.5.1, poluchim dispersionnoe uravnenie
gde
V predele ![]() poluchaem
poluchaem
4.5.6 Neodnorodnye gazovye diski s dvugorbymi krivymi vrasheniya
Vyshe my rassmotreli predel'nyi sluchai sovmeshennyh razryvov v
raspredeleniyah
![]() i
i ![]() . Yasno, chto predpolozheniya o
razryvnosti opredelyayushih neustoichivost' ravnovesnyh parametrov i
sovmeshennosti etih razryvov sushestvenno idealiziruyut nablyudaemye
raspredeleniya. Krome togo, po krainei mere v Galaktike ne
vypolnyaetsya uslovie
. Yasno, chto predpolozheniya o
razryvnosti opredelyayushih neustoichivost' ravnovesnyh parametrov i
sovmeshennosti etih razryvov sushestvenno idealiziruyut nablyudaemye
raspredeleniya. Krome togo, po krainei mere v Galaktike ne
vypolnyaetsya uslovie ![]() const.
const.
Sleduet otmetit' eshe odno obstoyatel'stvo. Pri chislennom
modelirovanii processa vozbuzhdeniya spiral'nogo uzora v galaktike s
dvugorboi krivoi vrasheniya vyyasnilos', chto v odnorodnom (v
nachal'nyi moment) gazovom diske raskachka neustoichivosti privodit k
vozniknoveniyu v okrestnosti vnutrennego maksimuma
![]() rezkogo
gradienta plotnosti, napominayushego nablyudaemyi v Galaktike4.9 [361]. Poetomu ves'ma aktual'no issledovanie vliyaniya
skachka plotnosti na parametry vozbuzhdaemogo uzora.
rezkogo
gradienta plotnosti, napominayushego nablyudaemyi v Galaktike4.9 [361]. Poetomu ves'ma aktual'no issledovanie vliyaniya
skachka plotnosti na parametry vozbuzhdaemogo uzora.
Rassmotrim klass modelei, v kotorom raspredeleniya ravnovesnyh
termodinamicheskih velichin opredeleny sootnosheniem
Takim obrazom, po raspredeleniyu
Vyberem konkretnoe raspredelenie ![]() v vide centrirovannoi
na
v vide centrirovannoi
na ![]() i "razmazannoi" na oblast' shirinoi
i "razmazannoi" na oblast' shirinoi
![]() stupen'ki:
stupen'ki:
obespechivaet vyhod na "plato" pri dostatochnom udalenii ot centra (
Budem ishodit' iz uravnenii (4.5.32), (4.5.33). Dannaya
sistema dolzhna sluzhit' dlya opredeleniya kak sobstvennyh funkcii
![]() ,
, ![]() , tak i sobstvennogo znacheniya -- chastoty
, tak i sobstvennogo znacheniya -- chastoty
![]() . Prostoi analiz uravnenii (4.5.32) i (4.5.33) v predele
. Prostoi analiz uravnenii (4.5.32) i (4.5.33) v predele
![]() pokazyvaet, chto
pokazyvaet, chto
![]() ,
,
![]() . Asimptotika reshenii pri
. Asimptotika reshenii pri
![]() s uchetom svoistv nashei modeli imeet vid
s uchetom svoistv nashei modeli imeet vid
![]() . V etoi
asimptotike vybor znaka pered mnimoi edinicei v eksponente
obespechivaet ubyvanie amplitudy neustoichivyh (
. V etoi
asimptotike vybor znaka pered mnimoi edinicei v eksponente
obespechivaet ubyvanie amplitudy neustoichivyh (
![]() ) vozmushenii s udaleniem ot oblasti skachka
) vozmushenii s udaleniem ot oblasti skachka ![]() . Takim obrazom,
estestvennye granichnye usloviya dlya sistemy (4.5.32), (4.5.33) v
sluchae vozmushenii s
. Takim obrazom,
estestvennye granichnye usloviya dlya sistemy (4.5.32), (4.5.33) v
sluchae vozmushenii s ![]() imeyut sleduyushii vid:
imeyut sleduyushii vid:
Vliyanie vida krivoi
![]() na parametry neustoichivosti bylo
izucheno v p. 4.5.4. Poetomu zdes' zafiksiruem krivuyu vrasheniya:
na parametry neustoichivosti bylo
izucheno v p. 4.5.4. Poetomu zdes' zafiksiruem krivuyu vrasheniya: ![]() ;
;
![]() ;
;
![]() [vid
[vid
![]() pri
takih znacheniyah parametrov pokazan na ris. 4.14]. Chislo spiralei budem
polagat' ravnym dvum (
pri
takih znacheniyah parametrov pokazan na ris. 4.14]. Chislo spiralei budem
polagat' ravnym dvum (![]() ). Sosredotochim nashe vnimanie na parametrah
modeli gazovogo diska. K nim prezhde vsego otnositsya velichina
skachka poverhnostnoi plotnosti gaza
). Sosredotochim nashe vnimanie na parametrah
modeli gazovogo diska. K nim prezhde vsego otnositsya velichina
skachka poverhnostnoi plotnosti gaza ![]() . V Galaktike
. V Galaktike
![]() [70]. Parametr
[70]. Parametr ![]() [sm. (4.5.45)], opredelyayushii
velichinu radial'nogo gradienta davleniya, otnositsya, po-vidimomu,
k chislu trudnonablyudaemyh. Parametrom
[sm. (4.5.45)], opredelyayushii
velichinu radial'nogo gradienta davleniya, otnositsya, po-vidimomu,
k chislu trudnonablyudaemyh. Parametrom
![]() udobno opisyvat'
smeshenie centrov skachkov
udobno opisyvat'
smeshenie centrov skachkov ![]() i
i ![]() . Dlya znachenii parametrov
. Dlya znachenii parametrov
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() chislennoe reshenie postavlennoi vyshe zadachi tipa
Shturma-Liuvillya pokazyvaet, chto pri vseh znacheniyah rassmatrivaemyh
parametrov imeet mesto neustoichivost', privodyashaya k vozbuzhdeniyu
dvuhrukavnoi spirali [
chislennoe reshenie postavlennoi vyshe zadachi tipa
Shturma-Liuvillya pokazyvaet, chto pri vseh znacheniyah rassmatrivaemyh
parametrov imeet mesto neustoichivost', privodyashaya k vozbuzhdeniyu
dvuhrukavnoi spirali [
![]() ] [356]. Takaya rastushaya po
amplitude proporcional'no
] [356]. Takaya rastushaya po
amplitude proporcional'no
![]() spiral' vrashaetsya s
uglovoi skorost'yu
spiral' vrashaetsya s
uglovoi skorost'yu
![]() . Po povedeniyu sobstvennyh
funkcii
. Po povedeniyu sobstvennyh
funkcii ![]() v principe vozmozhno opredelenie dliny volny
spiral'nogo uzora
v principe vozmozhno opredelenie dliny volny
spiral'nogo uzora ![]() na izvestnom rasstoyanii ot centra diska. Eta
velichina, konechno, lokal'naya. V sluchae odnorodnogo diska rassmatrivaemaya
model' dlya
na izvestnom rasstoyanii ot centra diska. Eta
velichina, konechno, lokal'naya. V sluchae odnorodnogo diska rassmatrivaemaya
model' dlya ![]() ,
, ![]() daet
daet
![]() . Otklonenie
. Otklonenie ![]() ot velichiny
ot velichiny
![]() pochti na vsei ploskosti
pochti na vsei ploskosti
![]() neznachitel'no.
Tol'ko v oblasti parametrov gazovogo diska
neznachitel'no.
Tol'ko v oblasti parametrov gazovogo diska ![]() ,
,
![]() vozmozhno zametnoe uvelichenie uglovoi skorosti vrasheniya spiral'nogo uzora
vozmozhno zametnoe uvelichenie uglovoi skorosti vrasheniya spiral'nogo uzora
![]() po sravneniyu s
po sravneniyu s
![]() . Raschety pokazyvayut, chto
velichina
. Raschety pokazyvayut, chto
velichina ![]() takzhe slabo zavisit ot vseh parametrov modeli, krome
parametra
takzhe slabo zavisit ot vseh parametrov modeli, krome
parametra ![]() :
:
![]() pri
pri ![]() i
i
![]() pri
pri ![]() .
.
Takim obrazom, uchet real'nyh (konechnoi shiriny) skachkov
plotnosti v gazovom diske ne mozhet v ramkah lineinoi teorii
privesti k sushestvennomu izmeneniyu osnovnogo dinamicheskogo
parametra spiral'nogo uzora ![]() .
.
Mogut li kakie-nibud' drugie fizicheskie faktory privesti k
zametnomu umen'sheniyu velichiny ![]() ? Analogovoe modelirovanie
spiral'nogo uzora (sm. razd. 6.2) pokazyvaet razlichie mezhdu
predskazyvaemoi lineinoi teoriei velichinoi
? Analogovoe modelirovanie
spiral'nogo uzora (sm. razd. 6.2) pokazyvaet razlichie mezhdu
predskazyvaemoi lineinoi teoriei velichinoi
![]() i
ee eksperimental'nym znacheniem
i
ee eksperimental'nym znacheniem
![]() (
(
![]() )4.10. Pri etom shiriny skachkov uglovoi skorosti
)4.10. Pri etom shiriny skachkov uglovoi skorosti ![]() i
tolshiny sloya "melkoi vody"
i
tolshiny sloya "melkoi vody" ![]() -- analoga
-- analoga ![]() -- v eksperimentah
byli pochti odinakovymi, a sami skachki -- prakticheski sovmeshennymi.
Po-vidimomu, obsuzhdaemoe razlichie mezhdu
-- v eksperimentah
byli pochti odinakovymi, a sami skachki -- prakticheski sovmeshennymi.
Po-vidimomu, obsuzhdaemoe razlichie mezhdu
![]() i
i
![]() obuslovleno nelineinost'yu eksperimenta. Eto podtverzhdaetsya tem, chto
vysokomodovye vozmusheniya (chislo spiralei
obuslovleno nelineinost'yu eksperimenta. Eto podtverzhdaetsya tem, chto
vysokomodovye vozmusheniya (chislo spiralei ![]() ) obladayut maloi
amplitudoi i dlya nih razlichie eksperimental'nogo i teoreticheskogo
znachenii
) obladayut maloi
amplitudoi i dlya nih razlichie eksperimental'nogo i teoreticheskogo
znachenii ![]() sushestvenno men'she, chem v sluchae vozbuzhdeniya mody
sushestvenno men'she, chem v sluchae vozbuzhdeniya mody
![]() , obladayushei sravnitel'no bol'shei amplitudoi. V svyazi s
vysheskazannym osobuyu rol' v dal'neishem razvitii gidrodinamicheskoi
koncepcii proishozhdeniya spiral'nogo uzora budut, veroyatno, igrat'
sovershenstvovanie metodiki nablyudatel'nogo opredeleniya parametra
, obladayushei sravnitel'no bol'shei amplitudoi. V svyazi s
vysheskazannym osobuyu rol' v dal'neishem razvitii gidrodinamicheskoi
koncepcii proishozhdeniya spiral'nogo uzora budut, veroyatno, igrat'
sovershenstvovanie metodiki nablyudatel'nogo opredeleniya parametra
![]() i razvitie chislennogo eksperimenta.
i razvitie chislennogo eksperimenta.
4.5.7 Nizkochastotnaya centrobezhnaya neustoichivost'
Provedennoe vyshe rassmotrenie vyyavilo odnu neustoichivuyu modu,
podderzhivaemuyu pri
![]() centrobezhnym mehanizmom, a pri
centrobezhnym mehanizmom, a pri
![]() -- mehanizmom neustoichivosti Kel'vina-Gel'mgol'ca. V to zhe
vremya sushestvovanie naryadu s osnovnoi neustoichivoi modoi i ee
vysshih garmonik v ploskoparallel'nyh sverhzvukovyh potokah gaza --
horosho izvestnyi fakt (sm. [364-367], p. 5.3.2). V
osesimmetrichnyh sverhzvukovyh techeniyah s differencial'nym
vrasheniem vysshie neustoichivye garmoniki byli otkryty ne tak davno
v sistemah so stepennoi zavisimost'yu skorosti vrasheniya ot radiusa
vida
-- mehanizmom neustoichivosti Kel'vina-Gel'mgol'ca. V to zhe
vremya sushestvovanie naryadu s osnovnoi neustoichivoi modoi i ee
vysshih garmonik v ploskoparallel'nyh sverhzvukovyh potokah gaza --
horosho izvestnyi fakt (sm. [364-367], p. 5.3.2). V
osesimmetrichnyh sverhzvukovyh techeniyah s differencial'nym
vrasheniem vysshie neustoichivye garmoniki byli otkryty ne tak davno
v sistemah so stepennoi zavisimost'yu skorosti vrasheniya ot radiusa
vida
![]() ,
, ![]() (sm. [368-370], p. 5.3.3).
(sm. [368-370], p. 5.3.3).
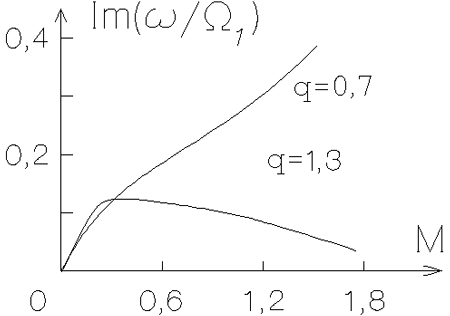
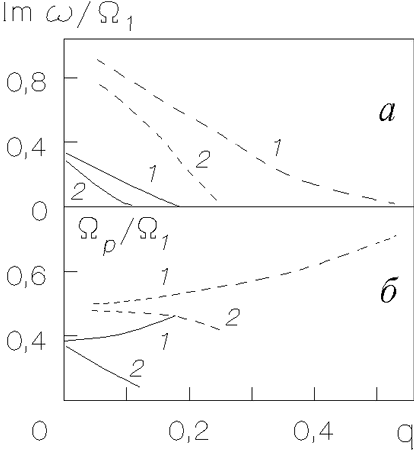 |
Ris. 4.15. Zavisimosti
bezrazmernogo inkrementa
|
V rabote [371] v ramkah modeli, opisyvaemoi uravneniyami
(4.5.32), (4.5.33), s krivoi vrasheniya (4.5.3), harakternoi dlya
gazovyh diskov galaktik, bylo pokazano nalichie vtoroi neustoichivoi
mody. Eta novaya dlya nas moda otlichaetsya ot rassmotrennoi vyshe
men'shimi znacheniyami kak
![]() , tak i
, tak i
![]() (ris. 4.15).
(ris. 4.15).
V sootvetstvii s etim osnovnuyu modu centrobezhnoi
neustoichivosti dalee budem nazyvat' vysokochastotnoi, a vtoruyu --
nizkochastotnoi. Krome togo, chto vysokochastotnaya moda obladaet
bol'shim inkrementom vo vsei rassmotrennoi oblasti znachenii
parametrov (sm. ris. 4.15), vozmusheniya etoi mody mogut narastat' v
teh diapazonah parametrov, gde nizkochastotnaya moda
stabiliziruetsya, a imenno pri men'shem skachke skorosti vrasheniya i
pri malyh chislah Maha (
![]() ). Razvitie vozmushenii obeih mod
privodit k generacii otstayushih logarifmicheskih spiral'nyh voln. V
dostatochno shirokoi oblasti znachenii parametrov zavisimosti
). Razvitie vozmushenii obeih mod
privodit k generacii otstayushih logarifmicheskih spiral'nyh voln. V
dostatochno shirokoi oblasti znachenii parametrov zavisimosti
![]() i
i
![]() ot
ot ![]() dlya obeih mod priblizitel'no
parallel'ny, prichem imeyutsya uchastki, gde razlichie ne prevyshaet 10
dlya obeih mod priblizitel'no
parallel'ny, prichem imeyutsya uchastki, gde razlichie ne prevyshaet 10
![]() 30 % [371]. Takim obrazom, pri opredelennyh usloviyah vozmozhno
ih odnovremennoe vozbuzhdenie.
30 % [371]. Takim obrazom, pri opredelennyh usloviyah vozmozhno
ih odnovremennoe vozbuzhdenie.
Morozov i Muscevoi [372] vyskazali predpolozhenie o
sushestvovanii analogichnyh vysokochastotnoi i nizkochastotnoi mod dlya
vozmushenii s ![]() dlya galakticheskih krivyh vrasheniya vida (4.5.3),
(4.5.48) (po
krainei mere, v modelyah so stepennymi zavisimostyami skorosti
vrasheniya ot
dlya galakticheskih krivyh vrasheniya vida (4.5.3),
(4.5.48) (po
krainei mere, v modelyah so stepennymi zavisimostyami skorosti
vrasheniya ot ![]() obnaruzhivaetsya celyi ryad neustoichivyh otrazhatel'nyh
garmonik dlya razlichnyh
obnaruzhivaetsya celyi ryad neustoichivyh otrazhatel'nyh
garmonik dlya razlichnyh ![]() (sm. p. 5.3.3)).
(sm. p. 5.3.3)).
Fizicheskii mehanizm raskachki nizkochastotnoi mody nosit
smeshannyi centrobezhno-rezonansnyi harakter, poetomu rassmotrennyi
sluchai imeet shodstvo so sluchaem modelei so stepennym zakonom
vrasheniya, gde neustoichivost' razvivaetsya iz-za rezonansnogo
izlucheniya energii na radiuse korotacii (na kotorom imeetsya
sinhronnoe vrashenie volnovogo uzora s veshestvom diska) i
vzaimodeistviya voln protivopolozhnyh znakov energii
(sverhotrazheniya). Vazhnost' centrobezhnyh effektov dlya podderzhaniya
nizkochastotnoi mody ochevidna, tak kak ona stabiliziruetsya pri
![]() . Na rezonansnyi harakter etoi mody ukazyvaet, v chastnosti, ee
stabilizaciya pri
. Na rezonansnyi harakter etoi mody ukazyvaet, v chastnosti, ee
stabilizaciya pri
![]() 4.11, poskol'ku dlya usileniya iz-za
rezonansnogo vzaimodeistviya volny s potokom neobhodimo nalichie
kriticheskogo sloya konechnoi tolshiny vblizi radiusa korotacii, gde
profil' skorosti yavlyaetsya monotonnym. Drugim dovodom yavlyaetsya ee
sushestvenno sverhzvukovoi harakter -- nizkochastotnaya moda
stabiliziruetsya pri umen'shenii chisla Maha do
4.11, poskol'ku dlya usileniya iz-za
rezonansnogo vzaimodeistviya volny s potokom neobhodimo nalichie
kriticheskogo sloya konechnoi tolshiny vblizi radiusa korotacii, gde
profil' skorosti yavlyaetsya monotonnym. Drugim dovodom yavlyaetsya ee
sushestvenno sverhzvukovoi harakter -- nizkochastotnaya moda
stabiliziruetsya pri umen'shenii chisla Maha do ![]() , chto sovpadaet
s porogovym znacheniem dlya sverhotrazheniya, kogda rezonansnoe
usilenie stanovitsya nevozmozhnym (sm. ris. 4.15) [327,373,374] (sm.
razd. 5.3).
, chto sovpadaet
s porogovym znacheniem dlya sverhotrazheniya, kogda rezonansnoe
usilenie stanovitsya nevozmozhnym (sm. ris. 4.15) [327,373,374] (sm.
razd. 5.3).
Sleduet otmetit', chto dlya raskachki nizkochastotnoi mody
principial'no neobhodimo libo vypolnenie usloviya
![]() , no ne
, no ne
![]() , t.e. nalichie konechnoi "razmazki" skachka skorosti,
libo pri
, t.e. nalichie konechnoi "razmazki" skachka skorosti,
libo pri
![]() nalichie vnutrennei otnositel'no razryva
skorosti otrazhayushei poverhnosti (tverdoi stenki ili skachka plotnosti),
raspolozhennoi na takom radiuse
nalichie vnutrennei otnositel'no razryva
skorosti otrazhayushei poverhnosti (tverdoi stenki ili skachka plotnosti),
raspolozhennoi na takom radiuse ![]() , chto ne imeet mesta uslovie
, chto ne imeet mesta uslovie
![]() (vypisannoe zdes' sootnoshenie
(vypisannoe zdes' sootnoshenie
![]() analogichno
usloviyu, pri kotorom mozhet byt' neustoichiv ploskii sloi sdviga:
analogichno
usloviyu, pri kotorom mozhet byt' neustoichiv ploskii sloi sdviga:
![]() , gde
, gde ![]() -- volnovoe chislo vozmushenii vdol' sloya,
-- volnovoe chislo vozmushenii vdol' sloya, ![]() --
ego harakternaya tolshina; poslednee utverzhdenie ochevidno, esli uchest', chto
velichina
--
ego harakternaya tolshina; poslednee utverzhdenie ochevidno, esli uchest', chto
velichina ![]() imeet smysl azimutal'nogo volnovogo chisla). Iz skazannogo
yasno, chto spiral'nye uzory, obuslovlennye nizkochastotnoi modoi, ne mogli
nablyudat'sya v eksperimentah s "melkoi vodoi" (gl. 6), poskol'ku v nih,
voobshe govorya, ne vypolnyalos' ni odno iz ukazannyh uslovii.
imeet smysl azimutal'nogo volnovogo chisla). Iz skazannogo
yasno, chto spiral'nye uzory, obuslovlennye nizkochastotnoi modoi, ne mogli
nablyudat'sya v eksperimentah s "melkoi vodoi" (gl. 6), poskol'ku v nih,
voobshe govorya, ne vypolnyalos' ni odno iz ukazannyh uslovii.
<< 4.4 Dissipativnye effekty | Oglavlenie | 4.6 Neosesimmetrichnyi potencial >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |