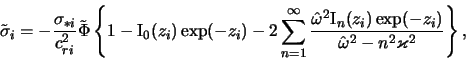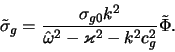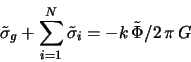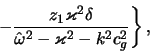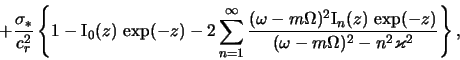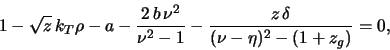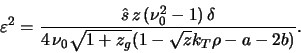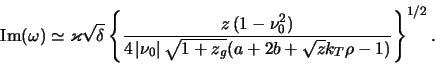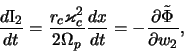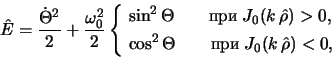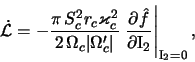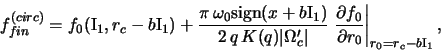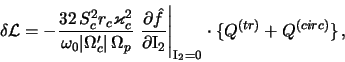<< 6. Priroda spiral'nogo uzora | Oglavlenie | 6.2 Gidrodinamicheskaya koncepciya ... >>
- 6.1.1 Mehanizm gravitacionnoi neustoichivosti na periferii bogatogo gazom diska
- 6.1.2 Rol' zvezdoobrazovaniya
- 6.1.3 Rezonans radial'nogo potoka gaza s gravitacionnoi spiral'noi volnoi
- 6.1.4 Nelineinoe nasyshenie rezonansnogo usileniya spiral'nyh voln na korotacionnom radiuse
6.1 Problemy vozbuzhdeniya gravitacionnyh voln plotnosti
6.1.1 Mehanizm gravitacionnoi neustoichivosti na periferii bogatogo gazom diska
Naselenie diskov galaktik neodnorodno po svoim dinamicheskim harakteristikam -- parcial'nym vkladam v polnuyu poverhnostnuyu plotnost' diska i dispersiyam skorostei sostavlyayushih ego ob'ektov. Tak, podsistemy dovol'no molodyh zvezd rannih spektral'nyh klassov (O, B, A) harakterizuyutsya maloi poverhnostnoi plotnost'yu i malymi dispersiyami skorostei, v to vremya kak podsistemy staryh zvezd gorazdo bolee massivny i dispersii ih radial'nyh skorostei veliki [53]. Otnositel'nyi zhe vklad gazovoi podsistemy v polnuyu plotnost' diska rastet s udaleniem ot centra pri prakticheski postoyannoi dispersii skorostei gazovyh oblakov (mnogo men'shei dispersii skorostei staryh zvezd).
Issleduem dinamiku malyh vozmushenii gravitacionnogo tipa v
ploskosti takogo mnogokomponentnogo diska, prenebregaya v pervom
priblizhenii radial'noi neodnorodnost'yu ego ravnovesnyh parametrov
(![]() , gde
, gde ![]() -- volnovoe chislo,
-- volnovoe chislo, ![]() -- masshtab radial'noi
neodnorodnosti diska). Eto
priblizhenie pozvolyaet isklyuchit' iz rassmotreniya vetvi
gradientnogo tipa i tem samym izuchit' nezavisimo vazhnye dlya teorii
Lina i Shu [196,197] dispersionnye svoistva gravitacionnyh
spiral'nyh voln plotnosti.
Eta zadacha byla vpervye postavlena Linom
i Shu [197] (imi byl issledovan dvuhkomponentnyi zvezdno-gazovyi
disk s
-- masshtab radial'noi
neodnorodnosti diska). Eto
priblizhenie pozvolyaet isklyuchit' iz rassmotreniya vetvi
gradientnogo tipa i tem samym izuchit' nezavisimo vazhnye dlya teorii
Lina i Shu [196,197] dispersionnye svoistva gravitacionnyh
spiral'nyh voln plotnosti.
Eta zadacha byla vpervye postavlena Linom
i Shu [197] (imi byl issledovan dvuhkomponentnyi zvezdno-gazovyi
disk s
![]() ), a izlagaemye nizhe
rezul'taty polucheny v [486].
), a izlagaemye nizhe
rezul'taty polucheny v [486].
Ravnovesnye funkcii raspredeleniya zvezd polagaem
shvarcshil'dovskimi (sm. p. 2.1.2) s parcial'nymi
poverhnostnymi plotnostyami zvezdnyh podsistem
![]()
![]() i sootvetstvuyushimi dispersiyami radial'nyh
skorostei
i sootvetstvuyushimi dispersiyami radial'nyh
skorostei ![]() . Gazovuyu podsistemu harakterizuem analogichnymi
parametrami
. Gazovuyu podsistemu harakterizuem analogichnymi
parametrami ![]() ,
, ![]() . V prinyatom priblizhenii vozmushennaya plotnost'
. V prinyatom priblizhenii vozmushennaya plotnost'
![]() -i zvezdnoi podsistemy
-i zvezdnoi podsistemy
![]() svyazana s vozmushennym
gravitacionnym potencialom
svyazana s vozmushennym
gravitacionnym potencialom ![]() sootnosheniem (sm. p. 2.2.2)
sootnosheniem (sm. p. 2.2.2)
Podstavlyaya zatem v uravnenie Puassona dlya mnogokomponentnogo diska
vyrazheniya (6.1.1), (6.1.2), poluchim iskomoe dispersionnoe uravnenie
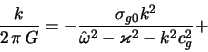
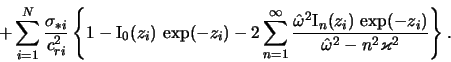
Dal'neishii analiz provedem v ramkah modeli dvuhkomponentnogo zvezdnogo diska
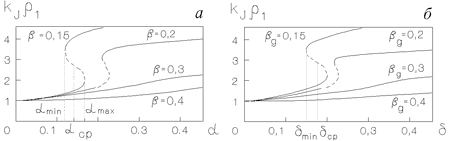 |
Ris. 6.1. Zavisimost' obratnogo
dzhinsovskogo masshtaba |
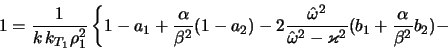
gde
Granica gravitacionnoi ustoichivosti rassmatrivaemoi modeli
diska opredelyaetsya iz usloviya
![]() v minimume dispersionnoi
krivoi
v minimume dispersionnoi
krivoi
![]() . Uslovie
. Uslovie
![]() poluchaem neposredstvenno iz (6.1.5):
poluchaem neposredstvenno iz (6.1.5):
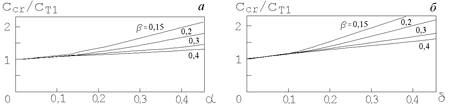 |
Ris. 6.2. Zavisimost'
neobhodimoi dlya marginal'noi
ustoichivosti diska kak celogo
dispersii radial'nyh skorostei
v massivnoi podsisteme staryh
zvezd (
|
Sovmestnoe reshenie sistemy (6.1.6), (6.1.7) opredelyaet
dzhinsovskii masshtab
![]() (masshtab marginal'no ustoichivyh
vozmushenii) i uslovie marginal'noi ustoichivosti diska. V
chastnosti, dlya odnokomponentnogo zvezdnogo diska (
(masshtab marginal'no ustoichivyh
vozmushenii) i uslovie marginal'noi ustoichivosti diska. V
chastnosti, dlya odnokomponentnogo zvezdnogo diska (
![]() ) iz
etoi sistemy vytekaet izvestnyi rezul'tat Toomre [202]
) iz
etoi sistemy vytekaet izvestnyi rezul'tat Toomre [202]
V kachestve pervogo primera rassmotrim model', v kotoroi disk-I
predstavlyaet soboi massivnuyu i "goryachuyu" podsistemu
staryh zvezd, disk-II -- malomassivnuyu i "holodnuyu"
podsistemu molodyh zvezd (![]() ,
, ![]() ), a gazovoi podsistemy
net (
), a gazovoi podsistemy
net (![]() ). Rezul'taty resheniya sistemy (6.1.6), (6.1.7) v ramkah
etoi modeli predstavleny na ris. 6.1,a i 6.2,a. Iz
ris. 6.1,a vidno, chto pri
). Rezul'taty resheniya sistemy (6.1.6), (6.1.7) v ramkah
etoi modeli predstavleny na ris. 6.1,a i 6.2,a. Iz
ris. 6.1,a vidno, chto pri
![]() zavisimost'
zavisimost'
![]() odnoznachna, i s rostom
odnoznachna, i s rostom
![]() i umen'sheniem
i umen'sheniem
![]() granica ustoichivosti diska smeshaetsya v korotkovolnovuyu oblast',
no neznachitel'no. Pri perehode k men'shim znacheniyam
granica ustoichivosti diska smeshaetsya v korotkovolnovuyu oblast',
no neznachitel'no. Pri perehode k men'shim znacheniyam
![]() proishodit kachestvennoe izmenenie -- zavisimost'
proishodit kachestvennoe izmenenie -- zavisimost'
![]() stanovitsya neodnoznachnoi: v nekotoroi oblasti po parametru
stanovitsya neodnoznachnoi: v nekotoroi oblasti po parametru ![]() [
[
![]() ] uravnenie (6.1.7)
imeet tri veshestvennyh kornya. Dva iz nih sootvetstvuyut dvum minimumam na
dispersionnoi krivoi
] uravnenie (6.1.7)
imeet tri veshestvennyh kornya. Dva iz nih sootvetstvuyut dvum minimumam na
dispersionnoi krivoi
![]() , a tretii -- maksimumu
mezhdu nimi (na ris. 6.1,a -- punktirom). Dlinnovolnovyi minimum
obuslovlen massivnoi podsistemoi staryh zvezd, i on opredelyaet marginal'nuyu
ustoichivost' diska s
, a tretii -- maksimumu
mezhdu nimi (na ris. 6.1,a -- punktirom). Dlinnovolnovyi minimum
obuslovlen massivnoi podsistemoi staryh zvezd, i on opredelyaet marginal'nuyu
ustoichivost' diska s
![]() (sm. ris. 6.1,a). Korotkovolnovyi
zhe minimum sozdaetsya "holodnoi" podsistemoi molodyh zvezd. Pri
(sm. ris. 6.1,a). Korotkovolnovyi
zhe minimum sozdaetsya "holodnoi" podsistemoi molodyh zvezd. Pri
![]() dispersionnaya krivaya
dispersionnaya krivaya
![]() vnov' imeet odin minimum, lezhashii uzhe v korotkovolnovoi oblasti i
obuslovlennyi malomassivnoi "holodnoi" podsistemoi zvezd.
vnov' imeet odin minimum, lezhashii uzhe v korotkovolnovoi oblasti i
obuslovlennyi malomassivnoi "holodnoi" podsistemoi zvezd.
Ris. 6.1,a yarko demonstriruet interesnuyu osobennost' sostavnoi
(dvuhkomponentnoi) modeli gravitiruyushego diska: esli odna iz
podsistem dostatochno "holodna" (
![]() ), to dazhe buduchi
ves'ma malomassivnoi (
), to dazhe buduchi
ves'ma malomassivnoi (
![]() ) imenno ona
opredelyaet velichinu dzhinsovskogo masshtaba
) imenno ona
opredelyaet velichinu dzhinsovskogo masshtaba ![]() i
ustoichivost' diska v celom. V svyazi s
etim sleduet otmetit', chto esli obe podsistemy budut v dostatochnoi
mere "ohlazhdennymi", to v oboih minimumah dispersionnoi krivoi
mozhet okazat'sya
i
ustoichivost' diska v celom. V svyazi s
etim sleduet otmetit', chto esli obe podsistemy budut v dostatochnoi
mere "ohlazhdennymi", to v oboih minimumah dispersionnoi krivoi
mozhet okazat'sya
![]() . Takim obpazom mogut voznikat'
dve izolipovannye
. Takim obpazom mogut voznikat'
dve izolipovannye ![]() -oblasti (dva kol'ca na
-oblasti (dva kol'ca na ![]() -ploskosti) neustoichivyh
vozmushenii. Eto oznachaet, chto v takom diske smogut vozbuzhdat'sya
struktury s dvumya sil'no razlichayushimisya prostranstvennymi
masshtabami (
-ploskosti) neustoichivyh
vozmushenii. Eto oznachaet, chto v takom diske smogut vozbuzhdat'sya
struktury s dvumya sil'no razlichayushimisya prostranstvennymi
masshtabami (
![]() ). V obshem zhe
sluchae
). V obshem zhe
sluchae ![]() -komponentnogo diska pri opredelennyh ogranicheniyah na
znacheniya parametrov podsistem mogut vozniknut'
-komponentnogo diska pri opredelennyh ogranicheniyah na
znacheniya parametrov podsistem mogut vozniknut' ![]() izolirovannyh
izolirovannyh
![]() -oblastei gravitacionno neustoichivyh vozmushenii [355].
-oblastei gravitacionno neustoichivyh vozmushenii [355].
Znachenie velichiny
![]() , neobhodimoi dlya marginal'noi
ustoichivosti diska kak celogo pri fiksirovannom
, neobhodimoi dlya marginal'noi
ustoichivosti diska kak celogo pri fiksirovannom
![]() ,
yavlyaetsya, ochevidno, takoi funkciei parametra
,
yavlyaetsya, ochevidno, takoi funkciei parametra ![]() , chto
, chto
![]() . Eta funkcional'naya
zavisimost' izobrazhena na ris. 6.2,a. Vidno, chto v oblasti
parametrov
. Eta funkcional'naya
zavisimost' izobrazhena na ris. 6.2,a. Vidno, chto v oblasti
parametrov
![]() eta zavisimost' okazyvaetsya dostatochno slaboi:
eta zavisimost' okazyvaetsya dostatochno slaboi:
![]() , t.e. v sootvetstvii s
rezul'tatom Toomre [202] velichina
, t.e. v sootvetstvii s
rezul'tatom Toomre [202] velichina
![]() .
Odnako esli odna iz podsistem dostatochno "holodna" (
.
Odnako esli odna iz podsistem dostatochno "holodna" (
![]() ),
to v oblasti
),
to v oblasti
![]() velichina
velichina ![]() rastet gorazdo
bystree s uvelicheniem parametra
rastet gorazdo
bystree s uvelicheniem parametra ![]() . Tem ne menee vazhno otmetit',
chto ustoichivost' diska s dovol'no massivnoi holodnoi podsistemoi II
(
. Tem ne menee vazhno otmetit',
chto ustoichivost' diska s dovol'no massivnoi holodnoi podsistemoi II
(
![]() ) mozhet byt' obespechena dostatochno goryachei podsistemoi
staryh zvezd.
) mozhet byt' obespechena dostatochno goryachei podsistemoi
staryh zvezd.
Rassmotrim teper' druguyu sostavnuyu model' -- dvuhkomponentnyi
zvezdno-gazovyi disk, sostoyashii iz podsistemy staryh zvezd
(
![]() ) i gazovoi podsistemy (
) i gazovoi podsistemy (
![]() ;
;
![]() ). Na pervyi
vzglyad mozhet pokazat'sya, chto rezul'taty issledovaniya takoi modeli
budut identichny rezul'tatam, poluchennym dlya dvuhkomponentnogo
zvezdnogo diska, s tochnost'yu do pereoboznachenii
). Na pervyi
vzglyad mozhet pokazat'sya, chto rezul'taty issledovaniya takoi modeli
budut identichny rezul'tatam, poluchennym dlya dvuhkomponentnogo
zvezdnogo diska, s tochnost'yu do pereoboznachenii
![]() ,
,
![]() . Odnako eto ne tak, poskol'ku dinamika
vozmushenii v gazovom diske opisyvaetsya gidrodinamicheskimi uravneniyami, a
v zvezdnom -- besstolknovitel'nym kineticheskim uravneniem, i kak raz v
oblasti dlin voln
. Odnako eto ne tak, poskol'ku dinamika
vozmushenii v gazovom diske opisyvaetsya gidrodinamicheskimi uravneniyami, a
v zvezdnom -- besstolknovitel'nym kineticheskim uravneniem, i kak raz v
oblasti dlin voln
![]() (ili
(ili
![]() )
eti sposoby opisaniya ne ekvivalentny. Poslednee obstoyatel'stvo okazyvaetsya
sushestvennym, potomu chto dazhe dlya naibolee "holodnyh" podsistem molodyh zvezd
i gaza
)
eti sposoby opisaniya ne ekvivalentny. Poslednee obstoyatel'stvo okazyvaetsya
sushestvennym, potomu chto dazhe dlya naibolee "holodnyh" podsistem molodyh zvezd
i gaza
![]() (zdes'
(zdes'
![]() ;
;
![]() -- dlina volny spiral'nogo uzora).
-- dlina volny spiral'nogo uzora).
Rezul'taty vychislenii v modeli zvezdno-gazovogo diska
izobrazheny na ris. 6.1,b, 6.2,b. Kachestvenno eti rezul'taty ne
otlichayutsya ot opisannyh vyshe dlya modeli dvuhkomponentnogo
zvezdnogo diska. Kolichestvennye zhe razlichiya sostoyat v sleduyushem.
Vo-pervyh, poyavlenie korotkovolnovogo minimuma proishodit pri
bol'shei otnositel'noi dole "holodnoi" (gazovoi) podsistemy:
![]() (sr.
ris. 6.1,a i
6.1,b). Vo-vtoryh, velichina neobhodimoi dlya marginal'noi
ustoichivosti diska
kak celogo
(sr.
ris. 6.1,a i
6.1,b). Vo-vtoryh, velichina neobhodimoi dlya marginal'noi
ustoichivosti diska
kak celogo
![]() s rostom parametra
s rostom parametra ![]() uvelichivaetsya sushestvenno bystree, chem s rostom parametra
uvelichivaetsya sushestvenno bystree, chem s rostom parametra
![]() v modeli dvuhkomponentnogo zvezdnogo diska
(sr. ris. 6.2,a i 6.2,b).
v modeli dvuhkomponentnogo zvezdnogo diska
(sr. ris. 6.2,a i 6.2,b).
Prezhde chem pereiti k konkretnym ocenkam v prilozhenii k
Galaktike, ostanovimsya eshe na trehkomponentnoi modeli diska
(starye zvezdy ![]() molodye zvezdy
molodye zvezdy ![]() gaz) i roli konechnoi tolshiny
podsistem. Budem schitat', chto legkaya podsistema molodyh zvezd (O,
V -- spektral'nyh tipov) obladaet toi zhe velichinoi dispersii
radial'nyh skorostei, chto i gaz, t.e.
gaz) i roli konechnoi tolshiny
podsistem. Budem schitat', chto legkaya podsistema molodyh zvezd (O,
V -- spektral'nyh tipov) obladaet toi zhe velichinoi dispersii
radial'nyh skorostei, chto i gaz, t.e.
![]() [53,70]. Togda rassmatrivaemaya model' harakterizuetsya tremya
parametrami:
[53,70]. Togda rassmatrivaemaya model' harakterizuetsya tremya
parametrami: ![]() ,
, ![]() ,
, ![]() . Rezul'taty issledovaniya etoi
modeli v naibolee interesnom predele
. Rezul'taty issledovaniya etoi
modeli v naibolee interesnom predele
![]() mozhno predstavit' v
sleduyushem vide. Zavisimost' obratnogo (normirovannogo) dzhinsovskogo
masshtaba
mozhno predstavit' v
sleduyushem vide. Zavisimost' obratnogo (normirovannogo) dzhinsovskogo
masshtaba ![]() ot parametrov modeli prakticheski sootvetstvuet
izobrazhennoi na ris. 6.1,b, esli po gorizontal'noi osi otkladyvat' ne
ot parametrov modeli prakticheski sootvetstvuet
izobrazhennoi na ris. 6.1,b, esli po gorizontal'noi osi otkladyvat' ne
![]() , a summu
, a summu
![]() . Velichina
. Velichina
![]() blizka k izobrazhennoi na ris. 6.2,b,
no neskol'ko men'she.
blizka k izobrazhennoi na ris. 6.2,b,
no neskol'ko men'she.
Odnako naibolee sushestvennoe vliyanie na privedennye vyshe
rezul'taty okazyvaet uchet konechnoi tolshiny podsistem diska. Sposob
ucheta etih velichin izvesten (sm. pp. 2.3.2, 4.2.2), i
sootvetstvuyushie vychisleniya [487] pokazali, chto pri razumnyh
znacheniyah
![]() i
i
![]() velichina
velichina
![]() (korotkovolnovyi minimum stanovitsya glubzhe
dlinnovolnovogo, i imenno on opredelyaet granicu gravitacionnoi
ustoichivosti diska pri
(korotkovolnovyi minimum stanovitsya glubzhe
dlinnovolnovogo, i imenno on opredelyaet granicu gravitacionnoi
ustoichivosti diska pri
![]() ). Blizkie
rezul'taty byli takzhe polucheny Dzhogom i Solomonom [488], issledovavshimi
gravitacionnuyu neustoichivost' dvuhkomponentnoi modeli diska, v kotoroi i
zvezdnaya, i gazovaya podsistemy opisyvalis' v ramkah
gidrodinamicheskogo priblizheniya.
). Blizkie
rezul'taty byli takzhe polucheny Dzhogom i Solomonom [488], issledovavshimi
gravitacionnuyu neustoichivost' dvuhkomponentnoi modeli diska, v kotoroi i
zvezdnaya, i gazovaya podsistemy opisyvalis' v ramkah
gidrodinamicheskogo priblizheniya.
Na osnovanii etih rezul'tatov sdelaem predvaritel'nye ocenki
dlya Galaktiki v okrestnosti Solnca (gde i byl sformulirovan
"paradoks Toomre":
![]() -- sm. vvedenie k nastoyashei
glave. Po dannym naibolee pravdopodobnoi modeli Galaktiki [24],
-- sm. vvedenie k nastoyashei
glave. Po dannym naibolee pravdopodobnoi modeli Galaktiki [24],
![]() M
M![]() /pk
/pk![]() ;
; ![]() kpk;
kpk;
![]() (km/s)/kpk i, sledovatel'no, tol'ko po
starym zvezdam
(km/s)/kpk i, sledovatel'no, tol'ko po
starym zvezdam
![]() kpk
(otlichie ot ocenki Toomre
kpk
(otlichie ot ocenki Toomre
![]() kpk svyazano v
osnovnom s tem, chto im ispol'zovalas' model' Shmidta [291], v kotoroi
kpk svyazano v
osnovnom s tem, chto im ispol'zovalas' model' Shmidta [291], v kotoroi
![]() M
M![]() /pk
/pk![]() ). Plotnost' gaza [70]
). Plotnost' gaza [70]
![]() M
M![]() /pk
/pk![]() . Otsyuda
. Otsyuda
![]() ,
a
,
a
![]() (zdes' parametr
(zdes' parametr ![]() uchityvaet tol'ko O,V -- zvezdy s
uchityvaet tol'ko O,V -- zvezdy s
![]() km/s). Po starym zvezdam
km/s). Po starym zvezdam
![]() km/s [53], a po gazu
km/s [53], a po gazu
![]() km/s [84].
Takim obrazom, nizhnyaya ocenka
km/s [84].
Takim obrazom, nizhnyaya ocenka
![]() ,
i soglasno ris. 6.2,b
,
i soglasno ris. 6.2,b
![]() , a iz
ris. 6.1,b sleduet,
chto naibolee blizkii k granice ustoichivosti minimum dispersionnoi
krivoi
, a iz
ris. 6.1,b sleduet,
chto naibolee blizkii k granice ustoichivosti minimum dispersionnoi
krivoi
![]() -- dlinnovolnovyi s
-- dlinnovolnovyi s
![]() . Otsyuda poluchaem staryi rezul'tat
. Otsyuda poluchaem staryi rezul'tat
![]() km/s i "paradoks Toomre" v
okrestnosti Solnca ne snimaetsya. Analogichnye ocenki ne pozvolyayut
nadeyat'sya na preodolenie "paradoksa Toomre" i v oblasti
km/s i "paradoks Toomre" v
okrestnosti Solnca ne snimaetsya. Analogichnye ocenki ne pozvolyayut
nadeyat'sya na preodolenie "paradoksa Toomre" i v oblasti ![]() .
Takim obrazom, dlya vozbuzhdeniya spiral'nyh voln plotnosti
korotkovolnovoi gravitacionnoi neustoichivost'yu v Galaktike net
neobhodimoi doli "holodnyh" (gaza i molodyh zvezd) podsistem.
Podobnyi vyvod budet, po-vidimomu, spravedliv i dlya bol'shinstva
drugih ne slishkom bogatyh gazom galaktik.
.
Takim obrazom, dlya vozbuzhdeniya spiral'nyh voln plotnosti
korotkovolnovoi gravitacionnoi neustoichivost'yu v Galaktike net
neobhodimoi doli "holodnyh" (gaza i molodyh zvezd) podsistem.
Podobnyi vyvod budet, po-vidimomu, spravedliv i dlya bol'shinstva
drugih ne slishkom bogatyh gazom galaktik.
6.1.2 Rol' zvezdoobrazovaniya
Dlya dostatochno bogatyh gazom ploskih galaktik rassmotrennaya
vyshe korotkovolnovaya gravitacionnaya neustoichivost' mozhet,
po-vidimomu, vozbuzhdat' struktury, harakternye masshtaby kotoryh
poryadka dliny volny spiral'nogo uzora. Neyasnym, odnako, ostaetsya
mehanizm vozbuzhdeniya neustoichivosti, poskol'ku gravitacionnaya
neustoichivost' imeet tendenciyu k dostatochno bystromu
samopodavleniyu [189]. Obsudim s etoi tochki zreniya vozmozhnost'
vozbuzhdeniya gravitacionnoi neustoichivosti processom
zvezdoobrazovaniya. Vpervye na etu vozmozhnost' ukazal Kato
[489]. Im, v chastnosti, bylo pokazano, chto v modeli dvuhkomponentnogo
zvezdno-gazovogo diska s
![]() i
i
![]() rozhdenie zvezd iz gaza privodit
k raskachke gravitacionnoi neustoichivosti, inkrement kotoroi maksimalen dlya
vozmushenii dzhinsovskogo masshtaba (
rozhdenie zvezd iz gaza privodit
k raskachke gravitacionnoi neustoichivosti, inkrement kotoroi maksimalen dlya
vozmushenii dzhinsovskogo masshtaba (
![]() ).
).
Issleduem etot vopros v ramkah rassmotrennoi vyshe
trehkomponentnoi modeli zvezdno-gazovogo diska. Predpolozhim, chto v
nachal'nyi moment vremeni disk byl marginal'no ustoichiv, t.e.
![]() . Zatem v techenie promezhutka vremeni
. Zatem v techenie promezhutka vremeni ![]() chast' gaza prevratilas' v molodye zvezdy s
chast' gaza prevratilas' v molodye zvezdy s ![]() , t.e.
, t.e. ![]() i
i
![]() poluchili prirasheniya, svyazannye sootnosheniem
poluchili prirasheniya, svyazannye sootnosheniem
V sisteme s izmenennymi ![]() i
i ![]() dolzhna smestit'sya granica
ustoichivosti po dline volny na
dolzhna smestit'sya granica
ustoichivosti po dline volny na ![]() ot
ot ![]() i
i ![]() izmenit'sya na
velichinu
izmenit'sya na
velichinu ![]() . Esli pri
. Esli pri ![]() okazhetsya
okazhetsya ![]() , to sistema
v celom stanet neustoichivoi, tak kak
, to sistema
v celom stanet neustoichivoi, tak kak
![]() . Takim obrazom,
obuslovlennaya zvezdoobrazovaniem neustoichivost' voznikaet, esli
. Takim obrazom,
obuslovlennaya zvezdoobrazovaniem neustoichivost' voznikaet, esli
Takim obrazom, process zvezdoobrazovaniya privodit k raskachke gravitacionnoi neustoichivosti v pervonachal'no ustoichivom mnogokomponentnom galakticheskom diske. Pri etom, po-vidimomu, v diske galaktiki budut protekat' relaksacionnye processy, uvelichivayushie dispersii skorostei ob'ektov sostavlyayushih disk podsistem i, sledovatel'no, stremyashiesya vozvratit' sistemu k ustoichivomu sostoyaniyu. Odnako prodolzhayushiesya zvezdoobrazovanie i zapazdyvanie relaksacionnyh processov budut podderzhivat' takuyu "tleyushuyu" neustoichivost' vplot' do vyhoda diska na takoe stacionarnoe sostoyanie, v kotorom processy zvezdoobrazovaniya i razrusheniya zvezd okazhutsya vzaimno skompensirovannymi. Takim obrazom, process zvezdoobrazovaniya okazyvaetsya postoyanno deistvuyushim generatorom struktur dzhinsovskogo masshtaba v mnogokomponentnom diske. Velichina dzhinsovskogo masshtaba zavisit ot doli "holodnyh" podsistem v diske i ih "temperatury".
6.1.3 Rezonans radial'nogo potoka gaza s gravitacionnoi spiral'noi volnoi
Interesnym mehanizmom vozbuzhdeniya gravitacionnyh spiral'nyh
voln plotnosti mozhet byt' mehanizm, obuslovlennyi neustoichivostyami
v sisteme s otnositel'nym dvizheniem ee podsistem. Neustoichivosti
etogo tipa obychno nazyvayut puchkovymi. Vpervye, po-vidimomu, takoi
mehanizm byl izuchen [490] v gidrodinamicheskih modelyah
mnogokomponentnogo diska s vrashayushimisya s sushestvenno razlichnymi
uglovymi skorostyami podsistemami. Pozdnee Kato [491] rassmotrel
bolee realistichnuyu model' zvezdno-gazovogo diska, v kotorom gaz
pomimo uchastiya v obshem vrashenii diska ispytyvaet eshe
makroskopicheskoe dvizhenie v radial'nom napravlenii. Dispersionnoe
uravnenie etoi modeli imeet vid [sr. s (6.1.4)]
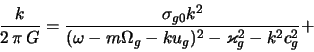
gde
Dispersionnoe uravnenie (6.1.10) bylo resheno Kato [491] chislenno lish' pri neskol'kih znacheniyah vhodyashih v nego parametrov, chto ne pozvolyaet ispol'zovat' poluchennye rezul'taty dlya vyyasneniya roli puchkovogo mehanizma v vozbuzhdenii spiral'nogo uzora razlichnyh galaktik. Privedem analiticheskoe issledovanie uravneniya (6.1.10) i sdelaem sootvetstvuyushie ocenki dlya Galaktiki [492].
Budem schitat', chto
![]() . Togda
. Togda
i tem samym mozhno polozhit'
gde
V sootvetstvii s dannymi nablyudenii polagaem
Tak kak
![]() i v ustoichivom po Toomre [202] diske
i v ustoichivom po Toomre [202] diske
![]() , iskomaya rezonansnaya puchkovaya
neustoichivost' (
, iskomaya rezonansnaya puchkovaya
neustoichivost' (
![]() ) imeet mesto pri
) imeet mesto pri
![]() (
(![]() ). Uslovie raskachki etoi neustoichivosti (uslovie rezonansa) imeet vid
). Uslovie raskachki etoi neustoichivosti (uslovie rezonansa) imeet vid
Dlya ocenki neobhodimoi dlya vozbuzhdeniya nablyudaemoi v
Galaktike spiral'noi struktury velichiny radial'noi skorosti
gazovogo potoka ![]() ispol'zuem privedennye v p. 6.1.1 dannye
nablyudenii i polagaem
ispol'zuem privedennye v p. 6.1.1 dannye
nablyudenii i polagaem
![]() kpk [493]. Schitaya spiral'
otstayushei i dvuhrukavnoi (
kpk [493]. Schitaya spiral'
otstayushei i dvuhrukavnoi (![]() ,
, ![]() ), iz (6.1.12) poluchaem
), iz (6.1.12) poluchaem
![]() (znak
(znak ![]() vybran v sootvetstvii s teoriei Lina i
Shu [482]), a iz (6.1.14) -- neobhodimuyu dlya vozbuzhdeniya spiralei
vybran v sootvetstvii s teoriei Lina i
Shu [482]), a iz (6.1.14) -- neobhodimuyu dlya vozbuzhdeniya spiralei
![]() km/s. Polagaya zatem
km/s. Polagaya zatem
![]() (sm. p. 6.1.1),
iz (6.1.15) poluchaem
(sm. p. 6.1.1),
iz (6.1.15) poluchaem
![]() . Takim obrazom, dazhe pri nalichii
neobhodimoi dlya raskachki issleduemoi neustoichivosti
. Takim obrazom, dazhe pri nalichii
neobhodimoi dlya raskachki issleduemoi neustoichivosti
![]() harakternoe vremya vozbuzhdeniya spiral'nogo uzora, ocenennoe
po maksimal'nomu inkrementu, ravno
harakternoe vremya vozbuzhdeniya spiral'nogo uzora, ocenennoe
po maksimal'nomu inkrementu, ravno ![]() oborotov diska, chto pochti v
dva raza prevyshaet vremya snosa volnovogo spiral'nogo paketa k
centru Galaktiki [453].
oborotov diska, chto pochti v
dva raza prevyshaet vremya snosa volnovogo spiral'nogo paketa k
centru Galaktiki [453].
Radial'nyh potokov gaza v okrestnosti Solnca s
![]() km/s, po-vidimomu, net. Otsyuda sleduet, chto mehanizm rezonansnoi
puchkovoi neustoichivosti radial'nogo potoka gaza v okrestnosti
km/s, po-vidimomu, net. Otsyuda sleduet, chto mehanizm rezonansnoi
puchkovoi neustoichivosti radial'nogo potoka gaza v okrestnosti ![]() ne mozhet byt' generatorom gravitacionnyh spiral'nyh voln
plotnosti. Otmetim takzhe, chto v ramkah teorii Lina i Shu
soglasno (6.1.14) rezonansnaya puchkovaya neustoichivost' mozhet imet'
mesto tol'ko v sluchae napravlennogo k centru Galaktiki radial'nogo
potoka gaza.
ne mozhet byt' generatorom gravitacionnyh spiral'nyh voln
plotnosti. Otmetim takzhe, chto v ramkah teorii Lina i Shu
soglasno (6.1.14) rezonansnaya puchkovaya neustoichivost' mozhet imet'
mesto tol'ko v sluchae napravlennogo k centru Galaktiki radial'nogo
potoka gaza.
Netrudno videt', chto minimal'no neobhodimaya dlya raskachki
rezonansnoi puchkovoi neustoichivost'yu gravitacionnyh spiral'nyh
voln plotnosti velichina
![]() mozhet byt' dostignuta na korotacionnom radiuse, gde
mozhet byt' dostignuta na korotacionnom radiuse, gde ![]() .
Absolyutnyi minimum
.
Absolyutnyi minimum
![]() dostigaetsya,
esli v etoi oblasti
dostigaetsya,
esli v etoi oblasti
![]() .
Takaya ocenka pokazyvaet, chto puchkovyi mehanizm
vryad li perspektiven kak mehanizm vozbuzhdeniya spiral'nogo uzora v
ploskih galaktikah.
.
Takaya ocenka pokazyvaet, chto puchkovyi mehanizm
vryad li perspektiven kak mehanizm vozbuzhdeniya spiral'nogo uzora v
ploskih galaktikah.
6.1.4 Nelineinoe nasyshenie rezonansnogo usileniya spiral'nyh voln na korotacionnom radiuse
Blagodarya differencial'nosti vrasheniya diska spiral'noi
galaktiki
![]() na nekotorom rasstoyanii ot ee centra
na nekotorom rasstoyanii ot ee centra
![]() uglovaya skorost' spiral'nogo uzora ravna
uglovaya skorost' spiral'nogo uzora ravna
![]() (velichinu
(velichinu ![]() nazyvayut korotacionnym radiusom).
Poetomu zvezdy diska,
lokalizovannye v okrestnosti korotacionnogo radiusa, okazyvayutsya v
rezonanse so spiral'noi volnoi. Linden-Bell i Kalnais [494]
pokazali, chto v ramkah lineinoi teorii takoe rezonansnoe
vzaimodeistvie volny so zvezdami diska privodit k usileniyu volny
(fizika etogo processa podrobno opisana Fridmanom i Polyachenko [2]).
nazyvayut korotacionnym radiusom).
Poetomu zvezdy diska,
lokalizovannye v okrestnosti korotacionnogo radiusa, okazyvayutsya v
rezonanse so spiral'noi volnoi. Linden-Bell i Kalnais [494]
pokazali, chto v ramkah lineinoi teorii takoe rezonansnoe
vzaimodeistvie volny so zvezdami diska privodit k usileniyu volny
(fizika etogo processa podrobno opisana Fridmanom i Polyachenko [2]).
Usilivayushayasya takim obrazom volna dolzhna okazyvat' vliyanie na dinamiku rezonansnyh zvezd, menyaya ih funkciyu raspredeleniya i tem samym usloviya usileniya volny. Poetomu yasno, chto issledovanie effektivnosti mehanizma rezonansnogo usileniya spiral'nyh gravitacionnyh voln na korotacionnom radiuse v nelineinom rezhime yavlyaetsya ves'ma aktual'nym. Provedem izuchenie etogo voprosa, sleduya rabote [495].
V sisteme otscheta, vrashayusheisya s uglovoi skorost'yu
spiral'nogo uzora ![]() , velichinu energii otdel'noi zvezdy mozhno
predstavit' v vide
, velichinu energii otdel'noi zvezdy mozhno
predstavit' v vide
gde
Uravneniya dvizheniya otdel'noi zvezdy vytekayut iz uravnenii
Gamil'tona:
![]() ;
;
![]() . Ogranichivayas' maloi okrestnost'yu korotacionnogo radiusa
. Ogranichivayas' maloi okrestnost'yu korotacionnogo radiusa
Iz (6.1.20), (6.1.22) vidno, chto uslovie rezonansa zvezdy v ploskosti (
Iz uravnenii (6.1.21), (6.1.22) sleduet, chto ![]() . Eto
obstoyatel'stvo pozvolyaet uprostit' zadachu, pereidya ot sistemy
(6.1.19)-(6.1.22), opisyvayushei dvizhenie otdel'noi zvezdy, k
uravneniyam, opisyvayushim dvizhenie centra ee epicikla. Takoi perehod
mozhet byt' vypolnen s pomosh'yu metoda usredneniya po "bystroi" faze
. Eto
obstoyatel'stvo pozvolyaet uprostit' zadachu, pereidya ot sistemy
(6.1.19)-(6.1.22), opisyvayushei dvizhenie otdel'noi zvezdy, k
uravneniyam, opisyvayushim dvizhenie centra ee epicikla. Takoi perehod
mozhet byt' vypolnen s pomosh'yu metoda usredneniya po "bystroi" faze
![]() , razrabotannogo Bogolyubovym i Mitropol'skim
[496]6.2. Dlya etogo
predstavim peremennye "deistvie-ugol" v vide
, razrabotannogo Bogolyubovym i Mitropol'skim
[496]6.2. Dlya etogo
predstavim peremennye "deistvie-ugol" v vide
![]() ;
;
![]() , gde
, gde
![]() ,
,
![]() opisyvayut "drozhatel'noe" dvizhenie s
bystroi fazoi
opisyvayut "drozhatel'noe" dvizhenie s
bystroi fazoi ![]() , a
, a ![]() ,
, ![]() -- plavnoe dvizhenie s
medlennoi fazoi
-- plavnoe dvizhenie s
medlennoi fazoi ![]() . Ostavlyaya v dal'neishih vychisleniyah dlya plavno menyayushihsya
velichin prezhnie oboznacheniya (bez znaka usredneniya), iz sistemy
(6.1.19)-(6.1.22) poluchim
. Ostavlyaya v dal'neishih vychisleniyah dlya plavno menyayushihsya
velichin prezhnie oboznacheniya (bez znaka usredneniya), iz sistemy
(6.1.19)-(6.1.22) poluchim
i, krome togo,
Predstavim gravitacionnyi potencial spiral'noi volny vo
vrashayusheisya s uglovoi skorost'yu ![]() sisteme otscheta v vide
sisteme otscheta v vide
gde velichina
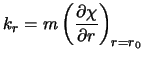 ;
;
Polagaya zatem bez ogranicheniya obshnosti
![]() i
oboznachaya fazu spiral'noi volny
i
oboznachaya fazu spiral'noi volny
![]() , privedem sistemu
(6.1.23), (6.1.24) k uravneniyu
, privedem sistemu
(6.1.23), (6.1.24) k uravneniyu
gde v sootvetstvii s nablyudeniyami schitalos' ![]() , a svyaz'
koordinat centra epicikla
, a svyaz'
koordinat centra epicikla ![]() ,
, ![]() s fazoi
s fazoi ![]() opredelyaetsya
sootnosheniyami
opredelyaetsya
sootnosheniyami
Uravnenie (6.1.28), k resheniyu kotorogo svelas' zadacha o
dvizhenii centra epicikla zvezdy v pole spiral'noi volny, imeet
integral energii
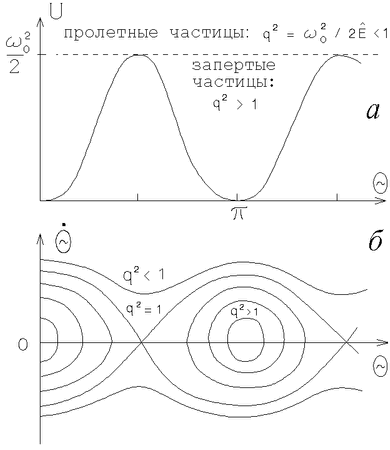 |
Ris. 6.3. a -- effektivnyi
potencial
|
Reshenie (6.1.28) mozhet byt' polucheno kak v ellipticheskih
funkciyah, tak i v bolee naglyadnom vide -- asimptoticheskom. Odnako
dazhe ne reshaya eto uravnenie, mozhno poluchit' kachestvennoe
predstavlenie o haraktere dvizheniya centrov epiciklov (v dal'neishem
dlya kratkosti -- chastic). Effektivnyi potencial [sm. (6.1.30)], v
kotorom dvizhutsya takie chasticy, izobrazhen na ris. 6.3,a. Vidno, chto
vse chasticy mozhno razdelit' na zapertye v volne, dlya kotoryh
![]() , i proletnye, dlya kotoryh
, i proletnye, dlya kotoryh ![]() .
Traektorii etih chastic na fazovoi ploskosti (
.
Traektorii etih chastic na fazovoi ploskosti (
![]() ) izobrazheny
na ris. 6.3,b.
) izobrazheny
na ris. 6.3,b.
Zapertye chasticy blagodarya tomu, chto effektivnyi potencial
(sm. ris. 6.3,a) ne yavlyaetsya kvadratichnym, v zavisimosti ot
velichiny parametra ![]() obladayut razlichnymi periodami dvizheniya po
koordinate
obladayut razlichnymi periodami dvizheniya po
koordinate ![]() . Takim obrazom, v okrestnosti korotacionnogo radiusa
voznikaet peremeshivanie chastic v fazovom prostranstve, v
rezul'tate chego na funkcii raspredeleniya etih chastic dolzhno
voznikat' plato za promezhutok vremeni poryadka
. Takim obrazom, v okrestnosti korotacionnogo radiusa
voznikaet peremeshivanie chastic v fazovom prostranstve, v
rezul'tate chego na funkcii raspredeleniya etih chastic dolzhno
voznikat' plato za promezhutok vremeni poryadka
![]() (izvestny analogichnye nelineinye effekty v plazme,
fizika etogo
processa prekrasno opisana Kadomcevym [497]).
(izvestny analogichnye nelineinye effekty v plazme,
fizika etogo
processa prekrasno opisana Kadomcevym [497]).
Esli oharakterizovat' intensivnost' volny bezrazmernoi
amplitudoi gravitacionnoi sily
![]() , to harakternoe
vremya
, to harakternoe
vremya
![]() , gde
, gde
![]() (po parametram spiral'nyh voln v
Galaktike
(po parametram spiral'nyh voln v
Galaktike
![]() ). Posle vozniknoveniya plato rost amplitudy
volny, obuslovlennyi gradientom funkcii raspredeleniya v fazovom
prostranstve, dolzhen prekratit'sya. Poetomu dlya proverki
effektivnosti predlozhennogo Linden-Bellom i Kalnaisom [494]
mehanizma usileniya spiral'nyh voln neobhodimo vychislit' amplitudu
nasysheniya volny k momentu "vyklyucheniya" etogo mehanizma i utochnit'
velichinu promezhutka vremeni ego raboty.
). Posle vozniknoveniya plato rost amplitudy
volny, obuslovlennyi gradientom funkcii raspredeleniya v fazovom
prostranstve, dolzhen prekratit'sya. Poetomu dlya proverki
effektivnosti predlozhennogo Linden-Bellom i Kalnaisom [494]
mehanizma usileniya spiral'nyh voln neobhodimo vychislit' amplitudu
nasysheniya volny k momentu "vyklyucheniya" etogo mehanizma i utochnit'
velichinu promezhutka vremeni ego raboty.
Spiral'naya volna, buduchi volnoi otricatel'noi energii v
oblasti ![]() , dolzhna rezonansnym obrazom usilivat'sya v
okrestnosti korotacionnogo radiusa za schet peredachi momenta
, dolzhna rezonansnym obrazom usilivat'sya v
okrestnosti korotacionnogo radiusa za schet peredachi momenta ![]() i
energii
i
energii ![]() rezonansnym zvezdam. Temp takoi peredachi v ramkah
lineinoi teorii opredelyaetsya sleduyushimi sootnosheniyami:
rezonansnym zvezdam. Temp takoi peredachi v ramkah
lineinoi teorii opredelyaetsya sleduyushimi sootnosheniyami:
gde
a
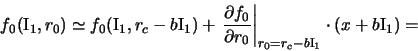
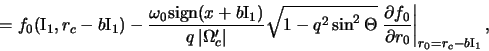
gde v
a funkciya raspredeleniya proletnyh chastic primet vid
gde
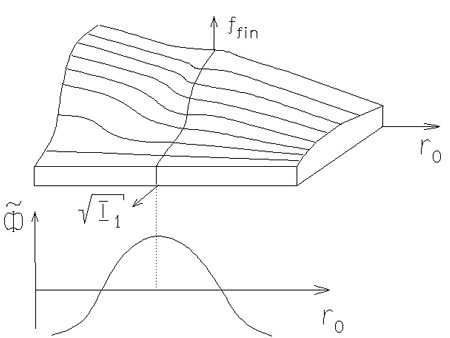 |
Ris. 6.4. Konechnaya
funkciya raspredeleniya
zvezd v napravlenii |
Naglyadnoe predstavlenie o funkcii raspredeleniya (6.1.36),
(6.1.37) mozhno poluchit' iz ris. 6.4. V kachestve nachal'noi funkcii
raspredeleniya
![]() pri postroenii etogo risunka byla vzyata
shvarcshil'dovskaya (2.1.44) s
pri postroenii etogo risunka byla vzyata
shvarcshil'dovskaya (2.1.44) s
![]() ;
;
![]() ;
;
![]() ;
; ![]() i parametrami volny
i parametrami volny
![]() ;
;
![]() [498]. Ris. 6.4 predstavlyaet
[498]. Ris. 6.4 predstavlyaet ![]() v
napravlenii
v
napravlenii ![]() v spiral'nom gravitacionnom potenciale
(6.1.26) s
v spiral'nom gravitacionnom potenciale
(6.1.26) s
![]() .
.
Velichinu peredannogo volne momenta ot rezonansnyh chastic
gde velichiny
harakterizuyut vklady v peredachu momenta i energii spiral'noi volne ot zapertyh i proletnyh chastic sootvetstvenno [
Iz sravneniya (6.1.32) s (6.1.39) sleduet
Predpolozhim teper', chto v Galaktike voznikli spiral'nye volny
beskonechno maloi amplitudy, i ocenim amplitudu ih nasysheniya
blagodarya rabote mehanizma rezonansnogo usileniya takih voln na
korotacionnom radiuse. Dlya etogo neobhodimo priravnyat' moment,
kotoryi mozhet byt' peredan volne rezonansnymi zvezdami (6.1.39),
momentu volny [194]
Togda po poryadku velichiny
Polagaya v (6.1.39) funkciyu raspredeleniya zvezd shvarcshil'dovskoi, poluchaem ocenku amplitudy nasysheniya volny
gde
Dlya obychno prinimaemogo v Galaktike znacheniya
![]() [498,500] eto daet
[498,500] eto daet
![]() , chto po krainei
mere na poryadok
men'she znachenii, poluchayushihsya v rezul'tate sravneniya raschetnyh i
nablyudaemyh kinematicheskih effektov, svyazannyh s dinamikoi
spiral'nyh voln v Galaktike.
, chto po krainei
mere na poryadok
men'she znachenii, poluchayushihsya v rezul'tate sravneniya raschetnyh i
nablyudaemyh kinematicheskih effektov, svyazannyh s dinamikoi
spiral'nyh voln v Galaktike.
Reshennaya zdes' zadacha blizka po smyslu k zadache o nelineinom
vzaimodeistvii sistemy zaryazhennyh chastic s volnoi elektricheskogo
potenciala [497]. V to zhe vremya v otlichie ot plazmy, gde v
rezonanse s volnoi okazyvaetsya malaya dolya chastic v prostranstve
skorostei, v nashem sluchae volna nahoditsya v rezonanse pochti so
vsemi chasticami skorostnogo prostranstva, lokalizovannymi, odnako,
v maloi okrestnosti korotacionnogo radiusa. Etot faktor "portit"
prostranstvennoe raspredelenie gravitacionnogo potenciala, i dlya
togo, chtoby ego vliyaniem mozhno bylo prenebrech', shirina
obrazuyushegosya plato ![]() dolzhna byt' mala po sravneniyu s dlinoi
volny
dolzhna byt' mala po sravneniyu s dlinoi
volny
![]() . Iz (6.1.29)-(6.1.31) sleduet ocenka
. Iz (6.1.29)-(6.1.31) sleduet ocenka
![]() , i poetomu
, i poetomu
![]() po parametram
spiral'noi struktury Galaktiki.
po parametram
spiral'noi struktury Galaktiki.
Neobhodimo takzhe otmetit', chto, soglasno Galeevu i Sagdeevu [501],
rezul'taty zadachi o narastanii volny do konechnoi amplitudy v
otlichie ot rezul'tatov zadachi o zatuhanii volny konechnoi amplitudy
sleduet rassmatrivat' lish' kak ocenku, poskol'ku pri vychislenii
dvizheniya chastic rostom potenciala prenebregali. Tem ne menee
poluchennyi zdes' vyvod o neeffektivnosti rezonansnogo usileniya
spiral'noi volny na korotacionnom radiuse veren, tak kak ocenka
amplitudy nasysheniya volny (6.1.46) pokazyvaet, chto
![]() .
.
Zametim eshe, chto v pohozhei na plazmennuyu postanovke v [502] byla reshena zadacha o nelineinom vzaimodeistvii puchka zvezd, dvizhushegosya vdol' osi samogravitiruyushego cilindra s volnoi, rasprostranyayusheisya v tom zhe napravlenii.
<< 6. Priroda spiral'nogo uzora | Oglavlenie | 6.2 Gidrodinamicheskaya koncepciya ... >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |