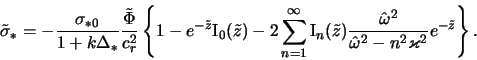<< 6.1 Vozbuzhdenie grav. voln plotnosti | Oglavlenie | 6.3 Slozhnye spiral'nye uzory >>
6.2 Gidrodinamicheskaya koncepciya obrazovaniya spiral'noi struktury
Na protyazhenii etoi knigi ne raz upominalos' o gidrodinamicheskoi koncepcii obrazovaniya spiral'nyh struktur ploskih galaktik. Soglasno etoi koncepcii, predlozhennoi A.M. Fridmanom v 1972 g., spiral'nye rukava predstavlyayut soboi volny plotnosti, narastayushie do nelineinyh amplitud iz-za razvitiya gidrodinamicheskih (nedzhinsovskih) neustoichivostei v gazovom galakticheskom diske. Razlichnym aspektam etoi koncepcii posvyashen ryad obzornyh statei i monografii [2,354,503-505].
V osnove etoi koncepcii lezhit sleduyushii fakt. Gazovyi disk
galaktiki, kak pravilo, obladaet massoi, mnogo men'shei massy
zvezdnogo diska (sm. p. 1.2.1) i, sledovatel'no,
. Iz etogo,
kazalos' by, dolzhen sledovat' vyvod, chto gaz ne vnosit zametnogo
vklada v gravitacionnyi potencial. Eto spravedlivo dlya
osesimmetrichnyh modelei. Odnako neobhodimo uchityvat', chto v
besstolknovitel'noi plazme zvezd vezde, krome central'nyh
oblastei 
galaktik, amplituda plotnosti neosesimmetrichnyh
osobennostei znachitel'no men'she polnoi plotnosti zvezdnogo diska
(
), togda kak v silu
stolknovitel'nosti gaza
rasprostranyayushiesya v nem vozmusheniya plotnosti mogut dostigat'
znachitel'nyh amplitud
(znachkom
" 
" pomecheny vozmushennye
velichiny). Esli znacheniya velichin 
i
sostavlyayut neskol'ko
procentov ot 
, to vozmozhna situaciya
, ili dazhe
(sm. [349,504]).
Pust' v gazovom diske vozniklo vozmushenie plotnosti. Dlya
ocenok (sm. podrobnee rabotu Fridmana [349]) vospol'zuemsya
vyrazheniem (4.2.11)
dlya vozmushennogo gravitacionnogo potenciala s
uchetom konechnoi tolshiny gazovogo diska
Prinimaya vo vnimanie uslovie
, kotoroe vypolnyaetsya dlya
Galaktiki [349], mozhno dlya ocenok prinyat'
.
Poslednee sootnoshenie sovmestno s (6.2.1) daet
V okrestnosti Solnca dlya dliny volny spiral'nogo uzora
kpk i znachenii
M
/pk
, 
km/s, 
pk,
pk poluchaem
V oblasti vnutrennego maksimuma na krivoi vrasheniya (
kpk)
eto otnoshenie okazyvaetsya eshe men'she [349]. Kak vidim, pri
issledovanii gidrodinamicheskih mehanizmov generacii spiral'noi
struktury mozhno v pervom priblizhenii ne uchityvat' vozmushenie
zvezdnoi podsistemy.
Naibolee veroyatnym pretendentom na rol' generatora spiral'noi struktury (po vremeni razvitiya i parametram voznikayushih spiralei v ramkah lineinogo analiza) sredi gidrodinamicheskih neustoichivostei yavlyaetsya centrobezhnaya. Eta neustoichivost' vozbuzhdaetsya v oblasti otricatel'nogo gradienta skorosti v galaktikah s dvugorbymi krivymi vrasheniya (v razd. 4.5 v ramkah razlichnyh modelei podrobno proanalizirovany usloviya vozniknoveniya centrobezhnoi neustoichivosti i svoistva voznikayushego spiral'nogo uzora).
Obsuzhdaemaya zdes' problema dopuskaet unikal'nuyu vozmozhnost' laboratornogo modelirovaniya ("galaktika na kuhonnom stole"). Nezlin i Snezhkin [505] podrobno opisali kak metodiku eksperimentov na ustanovke s vrashayusheisya "melkoi vodoi", tak i rezul'taty. Poetomu nizhe my kratko ostanovimsya tol'ko na osnovnyh momentah.
V osnove vozmozhnosti laboratornogo modelirovaniya spiral'nogo
galakticheskogo uzora lezhit ekvivalentnost' sistem uravnenii,
opisyvayushih dinamiku obshirnyh central'nyh oblastei gazovyh diskov
ploskih galaktik i tonkogo sloya vrashayusheisya neszhimaemoi zhidkosti.
Pri etom tolshina sloya zhidkosti 
sootvetstvuet poverhnostnoi
plotnosti szhimaemogo gaza, a rol' skorosti zvuka v gaze igraet
harakternaya skorost' voln na melkoi vode
[327].
Dlya modelirovaniya dvugorboi krivoi vrasheniya ("skachka" skorosti)
mozhno ispol'zovat' dva paraboloida, vrashayushihsya s razlichnoi
uglovoi skorost'yu. Provedennye opyty pokazali, chto razvitie
neustoichivosti privodit k vozniknoveniyu spiral'nyh voln
poverhnostnoi plotnosti razlichnyh azimutal'nyh mod (
). Spirali yavlyayutsya otstayushimi. Vrashenie spiral'nogo
uzora proishodit so skorost'yu, promezhutochnoi mezhdu skorostyami
vrasheniya central'noi chasti i periferii. Dlya opredelennoi mody
uglovaya skorost' vrasheniya spiral'nogo uzora 
yavlyaetsya monotonno
vozrastayushei funkciei ot chisla Maha (ris. 6.5). Kazhdaya moda mozhet
sushestvovat' tol'ko v opredelennom diapazone parametrov. Tak, v
usloviyah ris. 6.5 mody 
mogut realizovat'sya, esli
chislo Maha ne prevyshaet znachenii sootvetstvenno
. Kogda pri plavnom uvelichenii 
sistema prohodit cherez
eti granicy, nablyudaetsya perestroika dannoi mody v bolee
krupnomasshtabnuyu (
umen'shaetsya). Perestroika mod yavlyaetsya
sushestvenno nelineinym processom -- eto vidno uzhe iz togo, chto
perehody mezhdu modami imeyut skachkoobraznyi i gisterezisnyi
harakter. Obshaya zakonomernost' zaklyuchaetsya v tom, chto chislo
spiralei na perimetre sistemy umen'shaetsya pri uvelichenii chisla .
Sravnenie rezul'tatov laboratornyh eksperimentov s vyvodami
lineinoi teorii (rech' ne idet, razumeetsya, ob amplitude)
svidetel'stvuet o razlichiyah, ne prevyshayushih 30%.
 |
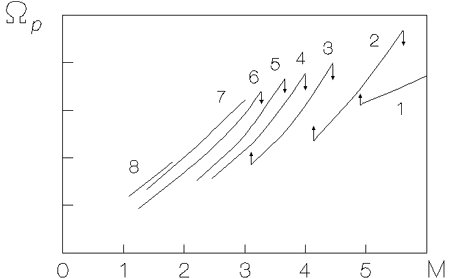Ris. 6.5. Uglovaya skorost'
vrasheniya spiral'nogo uzora
|
Pomimo centrobezhnoi neustoichivosti v ramkah
gidrodinamicheskoi koncepcii issleduyutsya i drugie. Mezhdu kraem
central'nogo molekulyarnogo diska i osobennost'yu na krivoi
vrasheniya (izlom ili skachok) obrazuetsya volnovodnyi sloi, v
kotorom mogut "raskachivat'sya" neustoichivosti rezonansnogo tipa,
analogichnye obsuzhdavshimsya v razd. 5.3 [506]. Drugoi vozmozhnyi
mehanizm -- rezonansno-centrobezhnyi, obsuzhdaetsya v razd. 4.5 i
6.3. K poyavleniyu krupnomasshtabnogo spiral'nogo uzora dolzhno
privodit' i razvitie mod neustoichivosti Papaloizu-Pringla s
nizshimi azimutal'nymi nomerami 
dazhe v diske bez
osobennostei na krivoi vrasheniya (sm. p. 5.3.3). Predlagalis' i
drugie gidrodinamicheskie mehanizmy [507].
<< 6.1 Vozbuzhdenie grav. voln plotnosti | Oglavlenie | 6.3 Slozhnye spiral'nye uzory >>
|
Publikacii s klyuchevymi slovami:
akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura
Publikacii so slovami: akkrecionnyi disk - disk, galakticheskii - gidrodinamika - spiral'naya struktura | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
