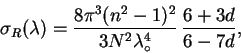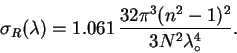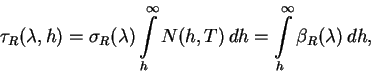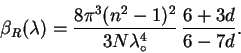Astronet > 4.2 Releevskoe rasseyanie

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 4.1 Prohozhdenie sveta cherez | Oglavlenie | 4.3 Rasseyanie na aerozolyah >>

4.2 Oslablenie sveta releevskim (molekulyarnym) rasseyaniem

Molekulyarnye fluktuacii plotnosti vozduha vyzyvayut rasseyanie svetovoi volny. Chast' sveta prodolzhaet rasprostranyat'sya v prezhnem napravlenii, a chast' -- raspredelyaetsya s razlichnoi intensivnost'yu pod vsemi uglami k etomu pervonachal'nomu napravleniyu (prichem chast' sveta rasseivaetsya nazad). Funkciya zavisimosti intensivnosti rasseyannogo sveta ot ugla rasseyaniya (t.e. ot ugla mezhdu napravleniem rasseyaniya i pervonachal'nym napravleniem) nazyvaetsya indikatrisoi rasseyaniya.

Formula dlya indikatrisy rasseyaniya v sluchae, kogda razmery rasseivayushih chastic maly po sravneniyu s dlinoi volny sveta, byla vpervye poluchena Releem (Rayleigh). Iz etoi formuly, neskol'ko vidoizmenennoi v rezul'tate dal'neishego utochneniya teorii rasseyaniya (s uchetom anizotropii molekul) sleduet, chto poperechnoe sechenie rasseyaniya $\sigma_R$ , rasschitannoe na odnu molekulu ravno

$\begin{displaymath} \sigma_R(\lambda) = \frac{8\pi^3(n^2-1)^2}{3N^2\lambda_{\circ}^4}\, \frac{6+3d}{6-7d} , \end{displaymath}$

(4.7)

zdes'

- pokazatel' prelomleniya vozduha,

- chislo molekul v 1sm ${}^3$ (chislo Loshmidta). Pri normal'nyh usloviyah (

= +15 ${}^{\circ}C$ ,

mbar),

= 2.687*10¹⁹sm^-3. Vtoroi somnozhitel' formuly vklyuchaet velichinu

, kotoraya dlya atmosfernogo vozduha ravna 0.035. Eto tak nazyvaemyi faktor depolyarizacii molekul.

Poskol'ku $n\approx1$ i $n^2-1\approx2(n-1)$ , to, uchityvaya, chto chlen s faktorom depolyarizacii dlya vozduha raven 1.061, formulu 4.7 mozhno zapisat' tak:

$\begin{displaymath} \sigma_R(\lambda) = 1.061\, \frac{32\pi^3(n^2-1)^2}{3N^2\lambda_{\circ}^4}. \end{displaymath}$

(4.8)

Chtoby poluchit' znachenie opticheskoi tolshi $\tau_R$ , obuslovlennoi releevskim rasseyaniem, dlya vsei atmosfery pri nablyudenii s vysoty nad urovnem morya, nuzhno poperechnoe sechenie rasseyaniya umnozhit' na kolichestvo chastic na puti lucha v vozduhe:

$\begin{displaymath} \tau_R(\lambda,h) = \sigma_R (\lambda) \int \limits_{h}^{\i... ...N(h,T)\,dh = \int \limits_{h}^{\infty} \beta_R(\lambda)\,dh , \end{displaymath}$

(4.9)

zdes'

- temperatura vozduha, a $\beta_R = \sigma(\lambda)N(h,T)$ - ob'emnyi (eksponencial'nyi) pokazatel' oslableniya sveta v vozduhe:

$\begin{displaymath} \beta_R(\lambda) = \frac{8\pi^3(n^2-1)^2}{3N\lambda_{\circ}^4}\, \frac{6+3d}{6-7d} . \end{displaymath}$

(4.10)

Sleduet obratit' vnimanie na to, chto pokazatel' oslableniya obratno proporcionalen chetvertoi stepeni dliny volny. Otsyuda sleduet, chto rasseyanie korotkovolnovogo izlucheniya proishodit sushestvenno bolee intensivno, chem dlinnovolnovogo. Imenno etim golubym rasseyannym svetom ob'yasnyaetsya cvet dnevnogo neba. Pri fotometricheskih izmereniyah vidno, chto i nochnoe nebo, podsvechennoe Lunoi, takzhe imeet goluboi ottenok: izmereniya fona neba pri nalichii Luny pokazyvayut, chto naibol'shii fon my imeem v sinih spektral'nyh polosah. Mozhet pokazat'sya strannym, chto kolichestvo molekul v edinice ob'ema stoit v formule v znamenatele. Eto sledstvie togo, chto velichina proporcional'na i v itoge $\beta_R(\lambda)$ proporcional'no , a ne . V formule imeetsya eshe nebol'shaya neyavnaya zavisimost' ot dliny volny, tak kak pokazatel' prelomleniya vozduha , strogo govorya, yavlyaetsya funkciei $\lambda$ .

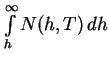Pri grubyh ocenkah velichinu integrala $\int \limits_{h}^{\infty} N(h,T)\,dh$ v formule (4.9) zamenyayut vysotoi odnorodnoi atmosfery. Eto uslovnaya atmosfera, v kotoroi s vysotoi plotnost' vozduha ne menyaetsya, a davlenie pri ee osnovanii ravno davleniyu pri osnovanii sootvetstvuyushego stolba vozduha v real'noi atmosfere. Pri zamene predpolagaetsya, chto chislo molekul, opredelyaemoe integralom v formule (4.9), ravno ih chislu v stolbe odnorodnoi atmosfery. Vysota odnorodnoi atmosfery vychislyaetsya po formule

$\begin{displaymath} H(h)=H(0)\,p(h)/p(0), \end{displaymath}$

(4.11)

gde

- vysota odnorodnoi atmosfery na urovne morya, a

- otnoshenie davleniya vozduha na vysote

k davleniyu na urovne morya. K sozhaleniyu, takaya ocenka dovol'no gruba, tak kak vysota odnorodnoi atmosfery na urovne morya zametno zavisit ot temperatury: izmenyaetsya pochti na 12% pri izmenenii temperatury ot $-15^{\circ}C$ do $+15^{\circ}C$ . Pri samyh tochnyh vychisleniyah po formule (4.7) uchityvayut takzhe zavisimosti pokazatelya prelomleniya vozduha ot vlazhnosti i davleniya. Eti formuly mozhno naiti, naprimer, v spravochnike K.U.Allena ``Astrofizicheskie velichiny'' (M.: Mir, 1977).

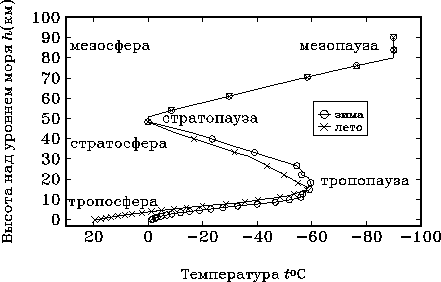
Raspredeleniya vlazhnosti, davleniya i temperatury s vysotoi nad urovnem morya v real'noi atmosfere yavlyayutsya dovol'no slozhnymi. Osobenno eto otnositsya k temperature, standartnyi hod kotoroi s vysotoi pokazan na ris.4.2.

Ris. 4.2: Raspredelenie srednei temperatury v atmosfere Zemli s vysotoi nad urovnem morya dlya letnego i zimnego sezonov

$\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig4_2.eps}\end{center}\end{figure}$

Vnachale, v troposfere, temperatura pochti lineino padaet s vysotoi. V raione tropopauzy (okolo 10 km) ona postoyanna i ravna priblizitel'no $-55^{\circ}C$ . Dalee, v stratosfere, temperatura nachinaet rasti i v stratopauze vnov' postoyanna i priblizitel'no ravna $0^{\circ}C$ . A zatem temperatura vnov' nachinaet padat' i dostigaet $-90^{\circ}C$ v mezopauze.

Neuchet vliyaniya raspredeleniya temperatury vozduha, davleniya i vlazhnosti s vysotoi na velichinu pokazatelya prelomleniya mozhet dat' oshibku (po krainei mere v neskol'ko desyatyh dolei procenta), kotoruyu uzhe sleduet uchityvat', esli vy hotite dostich' tochnosti, sravnimoi s apparaturnoi tochnost'yu sovremennyh fotometrov.

V poslednie gody na osnove novyh eksperimentov utochnyalas' zavisimost' pokazatelya prelomleniya ot dliny volny. S uchetom etih dannyh byla poluchena approksimaciya znachenii $\sigma(\lambda)$ :

(4.12)

gde $x = 0.389\lambda + 0.09426/\lambda - 0.3228$ dlya 0.2 $<\lambda<$ 0.55 mkm i x = 0.04 dlya 0.55 $<\lambda<$ 1 mkm. Pogreshnost' approksimacii sostavlyaet okolo 0.5%. Esli vychislen integral v formule (4.9) ili prinyato priblizhenie odnorodnoi atmosfery, to spektral'noe propuskanie atmosfery, oslablyayushei svet za schet releevskogo rasseyaniya, ravno

$\begin{displaymath} p_R(\lambda)=e^{-\tau_R(\lambda,h)} \end{displaymath}$

(4.13)

ili v zvezdnyh velichinah

$\begin{displaymath} \Delta m_R(\lambda) = -2.5\,\lg p_R(\lambda) \approx -1.086\,\tau_R(\lambda,h). \end{displaymath}$

(4.14)

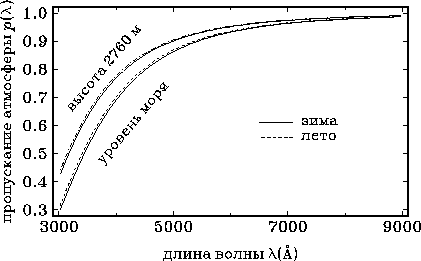
Vid funkcii $p_R(\lambda)$ pokazan na ris.4.3.

Ris. 4.3: Releevskoe oslablenie sveta

$\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig4_3.eps}\end{center}\end{figure}$

Eto plavnaya krivaya. V korotkovolnovoi oblasti oslablenie sostavlyaet bolee odnoi velichiny, togda kak oslableniem v dlinnovolnovoi dlya nekotoryh prilozhenii mozhno dazhe prenebrech': ono sostavlyaet 2-3%.

<< 4.1 Prohozhdenie sveta cherez | Oglavlenie | 4.3 Rasseyanie na aerozolyah >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce