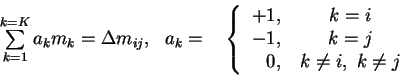Astronet > 5.7 Set' vtorichnyh standartov

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 5.6 Tyan'-Shan'skaya shirokopolosnaya ... | Oglavlenie | 6. Obrabotka izmerenii >>

5.7 O sozdanii seti vtorichnyh standartov

Esli v kazhdoi spektral'noi polose fotometricheskoi sistemy zadany v kachestve nul'-punkta vneatmosfernye zvezdnye velichiny odnoi izbrannoi zvezdy (ili summy vneatmosfernyh zvezdnyh velichin neskol'kih zvezd), to govoryat, chto zadan pervichnyi standart sistemy. So svetovym potokom ot etoi zvezdy -- pervichnogo standarta -- sleduet sravnivat' potoki ot vseh drugih zvezd, velichiny kotoryh zhelatel'no opredelit' v processe nablyudenii. Odnako takoe neposredstvennoe sravnenie daleko ne vsegda vozmozhno. Dlya prakticheskih nablyudenii neobhodimo imet' gorazdo bol'shee chislo zvezd, dlya kotoryh horosho opredeleny vneatmosfernye zvezdnye velichiny vo vseh polosah sistemy. Drugimi slovami, dlya nablyudenii nuzhno imet' set' vtorichnyh standartov.

Zvezdy, sostavlyayushie set' standartov fotometricheskoi sistemy, dolzhny udovletvoryat' neskol'kim usloviyam.

Vo-pervyh, oni dolzhny byt' dostatochno ravnomerno raspolozheny na nebesnoi sfere. Esli set' standartov sozdaetsya v sravnitel'no slabyh (m6) zvezdnyh velichinah, to eto uslovie vypolnit' neslozhno. Zhelatel'no, chtoby zvezdnye velichiny standartov i programmnyh zvezd razlichalis' ne bolee chem na 4-5 velichin.

Vo-vtoryh, dlya nih zhelatel'no znat' (hotya by s ne ochen' vysokoi tochnost'yu) raspredelenie energii v spektre $E(\lambda )$ ili, po krainei mere, horosho znat' ih spektral'nye tipy i byt' uverennym, chto raspredelenie energii ne imeet kakih-libo ekstravagantnyh osobennostei (tipa emissionnyh linii i t.p.). V sluchae neobhodimosti mozhno pol'zovat'sya normal'nym raspredeleniem energii v spektre, prinyatym dlya dannogo spektral'nogo tipa (naprimer iz kataloga Sviderskene). Esli vy pol'zuetes' normal'nym raspredeleniem energii, to, v svoyu ochered', nuzhna uverennost', chto mezhzvezdnoe pogloshenie dlya etogo standarta prakticheski otsutstvuet i ne iskazhaet vid funkcii $E(\lambda )$ . Zhelatel'no takzhe, chtoby raspredelenie energii v spektre bylo dostatochno gladkoi funkciei. V protivnom sluchae mogut vozniknut' slozhnosti pri primenenii tyan'-shan'skoi metodiki ucheta ekstinkcii (sm. gl. VI).

V tret'ih, standarty dolzhny byt' provereny na peremennost' i neobhodima uverennost', chto v predelah oshibok izmerenii net peremennosti v ispol'zuemyh nami intervalah spektra.

Na praktike, process sozdaniya seti vtorichnyh standartov razbivaetsya na neskol'ko etapov.

Na pervom etape vy, pol'zuyas' vsevozmozhnymi zvezdnymi katalogami, vybiraete kandidatov v standarty, po vozmozhnosti ravnomerno raspolozhennyh na nebe. Pri podbore sleduet pol'zovat'sya sleduyushimi kriteriyami.

Sredi kandidatov v standarty dolzhno byt' dostatochnoe kolichestvo zvezd s naibolee gladkimi raspredeleniyami energii. Eto zvezdy rannih spektral'nyh klassov. Obychno oni vybirayutsya iz zvezd glavnoi posledovatel'nosti v intervale spektral'nyh klassov B8-F5. Vmeste s tem izvestno, chto sredi zvezd etih spektral'nyh klassov neredko vstrechayutsya pul'siruyushie peremennye tipa $\delta$ Sct. Dlya etih zvezd harakterny amplitudy peremennosti $0{}^m\!\!\!.\,01$ - $0{}^m\!\!\!.\,1$ i periody 0.003-0.02 sutok. Otkryvat' maloamplitudnye peremennye trudno, poetomu sredi belyh zvezd eshe ochen' mnogo neotkrytyh peremennyh tipa $\delta$ Shita. Poetomu, sredi kandidatov v standarty dolzhno byt' takzhe dostatochno zvezd glavnoi posledovatel'nosti spektral'nyh klassov F5-K0. V etom intervale spektrov veroyatnost' vstretit' peremennost' s maloi amplitudoi gorazdo men'she. Bol'shie zhe amplitudy otkryvayutsya sravnitel'no prosto, i sredi dostatochno yarkih () zvezd neizvestnyh peremennyh s amplitudami bolee $0{}^m\!\!\!.\,1$ dolzhno byt' nemnogo.

Dalee, neobhodimo tshatel'no proverit', net li v literature ukazanii na peremennost' kazhdoi iz etih zvezd. Prezhde vsego nuzhno proverit', ne soderzhatsya li oni zvezd v ``Obshem kataloge peremennyh zvezd'' ili v ``Novom kataloge zvezd, zapodozrennyh v peremennosti''.

Na vtorom etape nuzhno provesti nablyudeniya etih kandidatov v standarty. Poskol'ku zvezdnye velichiny standartov dolzhny byt' izvestny s maksimal'no vysokoi tochnost'yu, nuzhno vybirat' samye horoshie nochi s samoi vysokoi stabil'nost'yu prozrachnosti. Obychno s vechera vy nachinaete nablyudat' kakie-libo programmnye zvezdy, i, esli ubezhdaetes', chto pri blizkih vozdushnyh massah izmereniya odnogo i togo zhe ob'ekta povtoryayutsya s razbrosom, ne prevoshodyashim 1to sleduet pereiti k nablyudeniyam standartov. Togda vy vybiraete paru kandidatov v standarty (s nomerami i ) i ``privyazyvaete'' ih drug k drugu, t.e. vedete nablyudeniya po sheme:

standart $i~\to$ fon u standarta $i~\to$ standart $j \to$ fon u standarta

Etot process sleduet povtorit' dva-tri raza. Vsya seriya izmerenii dolzhna byt' vypolnena dostatochno bystro, chtoby bylo osnovanie prenebrech' vozmozhnymi nebol'shimi izmeneniyami atmosfernoi prozrachnosti i chuvstvitel'nosti priemnoi apparatury. Chtoby pri obrabotke minimizirovat' oshibki vynosa za atmosferu, nablyudeniya sleduet stroit' v sootvetstvii s ``principom ravnyh vysot'', t.e. oba standarta pary, nablyudayusheisya v dannyi moment, dolzhny nahodit'sya na blizkih zenitnyh rasstoyaniyah. Zhelatel'no, chtoby razlichie vozdushnyh mass standartov ne prevyshalo $0{}^m\!\!\!.\,05$ . V observatoriyah, nahodyashihsya vyshe $40^{\circ}$ severnoi shiroty, pri privyazke standartov, imeyushih otricatel'nye skloneniya, etomu pravilu ne vsegda legko sledovat'. Sistematicheski nuzhno takzhe privyazyvat' vtorichnye standarty k pervichnomu.

Esli vy vedete katalozhnye nablyudeniya, to mozhno proizvodit' privyazki standartov drug k drugu odnovremenno s nablyudeniyami programmnyh zvezd. Dlya etogo nuzhno nablyudat' programmnye zvezdy ne s odnim, a s neskol'kimi (dvumya-chetyr'mya) standartami i sledit' za tem, chtoby v raznyh seriyah nablyudenii sostav takogo nabora chastichno izmenyalsya. Pri etom trudno dostich' strogogo soblyudeniya trebovaniya ravnyh vysot, no pri mnogochislennyh nablyudeniyah mozhno poluchit' dostatochnuyu tochnost'. Preimushestvo dannogo sposoba v tom, chto vy mozhete nablyudat' programmnye zvezdy do togo, kak budet polnost'yu sozdana i uvyazana set' vtorichnyh standartov. Na praktike primenyayut oba sposoba parallel'no.

Kogda nakopitsya dostatochnoe kolichestvo nablyudenii raznoobraznyh par standartov, mozhno pristupat' k tret'emu etapu: proizvesti nailuchshim obrazom uvyazku izmerennyh raznostei ih zvezdnyh velichin v edinuyu sistemu.

Posle obrabotki ravnovysotnyh nablyudenii i ucheta atmosfernoi ekstinkcii dlya kazhdoi serii i dlya kazhdoi fotometricheskoi polosy poluchayutsya uravneniya vida

$\begin{displaymath} m_i - m_j = \Delta m'_{ij} , \end{displaymath}$

(5.9)

gde

-- sootvetstvenno, neizvestnye vneatmosfernye velichiny

-go i

-go standartov v dannoi polose, a $\Delta m'_{ij}$ -- izmerennaya raznost' etih velichin v instrumental'noi sisteme.

Neobhodimo pomnit', chto snachala sleduet po formule (5.8) perevesti instrumental'nye raznosti $\Delta m'_{ij}$ v standartnye $\Delta m_{ij}$ .

Pust' u nas imeetsya razlichnyh standartov, s nomerami 1,2,3,..., kazhdyi iz kotoryh sravnivalsya ravnovysotnym metodom po krainei mere s dvumya drugimi standartami. Nekotorye iz nih sravnivalis' neposredstvenno s pervichnym standartom, velichiny kotorogo zadayut nul'-punkt fotometricheskoi sistemy. Pust', dalee, my vypolnili serii ravnovysotnyh privyazok par standartov. Togda u nas est' uslovnyh uravnenii tipa (5.9) s neizvestnymi. Chtoby privesti dvuchlennye uravneniya (5.9) k obshemu vidu dobavim v kazhdoe iz nih chleny s neizvestnymi zvezdnymi velichinami vseh ostal'nyh standartov, no snabdim ih nulevymi koefficientami:

$\begin{displaymath} m_i-m_j=0\times m_1+0\times m_2+\cdots+1\times m_i+\cdots -1\times m_j+\cdots+0\times m_K=\Delta m_{ij}. \end{displaymath}$

Drugimi slovami, transformiruem sistemu uravnenii vida (5.9) k vidu

$\begin{displaymath} \begin{array}{ll} \sum\limits_{k=1}^{k=K}a_km_k = \Delta m_{... ... $0$, & $k\neq i,\ k\neq j$\\ \end{tabular}\right. \end{array}\end{displaymath}$

(5.10)

Poskol'ku tochnost' izmerenii dlya razlichnyh par standartov mozhet byt' razlichnoi, kazhdomu uravneniyu (5.10) mozhno pripisat' ves. Pri naznachenii vesa sleduet prinimat' vo vnimanie razlichiya v konkretnyh usloviyah nablyudenii dlya kazhdoi pary: srednyuyu vozdushnuyu massu i razlichie vozdushnyh mass dvuh standartov v moment nablyudenii, uglovoe rasstoyanie mezhdu standartami, stabil'nost' atmosfernoi prozrachnosti i tak dalee.

Sistema (5.10) yavlyaetsya vyrozhdennoi. Opredelitel' matricy ee koefficientov raven nulyu. Chtoby reshit' etu sistemu, ee nuzhno dopolnit' eshe odnim uravneniem. V nashem sluchae eto uravnenie, zadayushee nul'-punkt i aksiomaticheski prisvaivayushee pervichnomu standartu znachenie ego zvezdnoi velichiny.

$\begin{displaymath} m_{0}^{st} = {\textrm const} \end{displaymath}$

(5.11)

Sistemu (5.10) s dopolnitel'nym uravneniem (5.11) mozhno reshit' sposobom naimen'shih kvadratov.

Pri reshenii mogut vozniknut' vychislitel'nye trudnosti, tak kak eto dovol'no bol'shaya sistema. V obychnyh usloviyah byvaet ot neskol'kih desyatkov do neskol'kih soten. -- neskol'ko tysyach. Tak, pri sozdanii seti standartov fotometricheskoi sistemy WBVR na pervom etape reshalas' sistema iz 980 uravnenii s 61 neizvestnym, a na vtorom etape -- iz 4200 uravnenii s 228 neizvestnymi.

V rezul'tate poluchayutsya uvyazannye vneatmosfernye velichiny vseh vtorichnyh standartov fotometricheskoi sistemy.

<< 5.6 Tyan'-Shan'skaya shirokopolosnaya ... | Oglavlenie | 6. Obrabotka izmerenii >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce