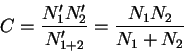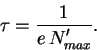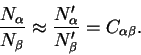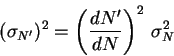Astronet > 6.2 Uchet nelineinosti

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 6.1 Zhurnal nablyudenii | Oglavlenie | 6.3 Uchet atmosfernoi ekstinkcii >>

Razdely

6.2 Uchet nelineinosti v metode scheta fotonov

Pervoe, chto nuzhno sdelat' pri redukciyah - eto uchest' nelineinost'. Pri rabote s usilitelyami postoyannogo toka etot vopros dovol'no slozhen. Ostanovimsya na poryadke ucheta nelineinosti pri izmereniyah po metodu scheta fotonov. V gl. III dlya ucheta etogo effekta my poluchili formuly (3.9), i (3.11). Zadacha tol'ko v tom, chtoby opredelit' velichinu parametra ``mertvogo vremeni'' $\tau$ . Eto mozhno sdelat' raznymi metodami.

6.2.1 Laboratornyi metod summy potokov

Pri ispytaniyah fotoumnozhitelei v laboratornyh usloviyah neslozhno opredelit' parametr $\tau$ , imeya special'no skonstruirovannyi osvetitel'. V etom osvetitele imeetsya dva istochnika sveta i est' vozmozhnost' osveshat' fotokatod FEU libo odnim istochnikom, libo vtorym, libo dvumya vmeste. Razumeetsya, nuzhno pozabotit'sya o tom, chtoby za vremya izmerenii osveshennost', sozdavaemaya kazhdym iz istochnikov byla postoyannoi.

Pust' na pervyi istochnik FEU reagiruet vydachei signala imp/s, a na vtoroi, sootvetstvenno, imp/s. Iz formuly (3.6) sleduet:

$\begin{displaymath} N'_1=N_1e^{-\tau N_1}, \end{displaymath}$

(6.1)

$\begin{displaymath} N'_2=N_2e^{-\tau N_2}. \end{displaymath}$

(6.2)

Esli osvetit' FEU summarnym svetom dvuh istochnikov, to zaregistrirovannomu otschetu $N'_{1+2}$ budet sootvetstvovat' istinnyi otschet

$\begin{displaymath} N'_{1+2}=(N_1+N_2)e^{-\tau(N_1+N_2)}. \end{displaymath}$

(6.3)

Tri uravneniya (6.1), (6.2) i (6.3) obrazuyut sistemu s tremya neizvestnymi

i $\tau$ . Reshaya ee odnim iz izvestnyh sposobov poluchaem parametr nelineinosti. Zametim, chto velichina

$\begin{displaymath} C = \frac{N'_1N'_2}{N'_{1+2}}=\frac{N_1 N_2}{N_1+N_2} \end{displaymath}$

(6.4)

ne zavisit ot znacheniya $\tau$ .

6.2.2 Metod maksimuma signala

Prodifferenciruem obe chasti formuly (3.6) po . Poluchim

$\begin{displaymath} \frac{dN'}{dN}=\frac{d~}{dN}(Ne^{-\tau N}) = (1-\tau N)e^{-\tau N}. \end{displaymath}$

(6.5)

Vyrazhenie v pravoi chasti ravno nulyu pri $\tau N=1$ , sledovatel'no funkciya

imeet maksimum pri $N_{max}=1/\tau$ .

Pri uvelichenii osveshennosti fotokatoda FEU snachala otschety rastut, zatem etot rost zamedlyaetsya i, nakonec, otschety nachinayut umen'shat'sya. Esli zaregistrirovat' etot maksimum, to

$\begin{displaymath} \tau = \frac{\displaystyle{1}}{\displaystyle e\,N'_{max}}. \end{displaymath}$

(6.6)

Nedostatkom metoda yavlyaetsya to, chto $N'_{max}$ dostigaetsya pri dostatochno yarkom osveshenii, chto nebezopasno dlya FEU. Pri bol'shih signalah model' nelineinosti, predstavlennaya formuloi (3.6), lish' priblizhenno sootvetstvuet real'nym processam, poetomu metod maksimuma signala pozvolyaet sdelat' lish' grubuyu ocenku $\tau$ .

6.2.3 Metod diafragmirovaniya glavnogo zerkala

Kogda vash fotometr visit na teleskope, laboratornye metody neudobny. Nuzhno umet' kontrolirovat' $\tau$ po zvezdam, ne snimaya apparaturu. Dlya etogo v raione zenita vybirayutsya dve blizkie po raspolozheniyu zvezdy (chtoby atmosfera vliyala na nih odinakovo), razlichayushiesya po zvezdnoi velichine na -. Obychno starayutsya podobrat' zvezdy odinakovogo spektral'nogo klassa, ili nablyudayut ih cherez uzkopolosnyi svetofil'tr.

Nesushestvenno, vo skol'ko raz budut razlichat'sya potoki ot nih, no sushestvenno, chto pri razlichnyh znacheniyah apertury teleskopa otnoshenie ih vneatmosfernyh potokov est' postoyannaya velichina. Izmenyat' aperturu mozhno raznymi sposobami. Naprimer, u teleskopov AZT-14 est' ochen' udobnoe ustroistvo: irisovaya diafragma na glavnom zerkale. Pri raznyh raskrytiyah diafragmy vy poluchite raznyi potok ot obeih zvezd.

Oboznachim dve vybrannye zvezdy bukvami $\alpha$ i $\beta$ . Zametim, chto pri malyh raskrytiyah diafragmy potoki budut maly, i nelineinost' prakticheski ne budet vliyat' na otschety i pri etom mozhno izmerit' istinnoe otnoshenie potokov ot dvuh zvezd

$\begin{displaymath} \frac{N_\alpha}{N_\beta}\approx\frac{N'_\alpha}{N'_\beta} = C_{\alpha\beta}. \end{displaymath}$

(6.7)

Zatem nuzhno poluchit' otschety pri neskol'kih drugih raskrytiyah diafragmy, v tom chisle pri polnost'yu otkrytom zerkale. Pust' my sdelali seriyu izmerenii obeih zvezd pri razlichnyh diafragmah s nomerami

. Dlya kazhdoi diafragmy v sootvetstvii v uravneniem (3.6) mozhno napisat':

(6.8)

(6.9)

Uravneniya (6.7), (6.8) i (6.9) sostavlyayut sistemu s tremya neizvestnymi, reshaya kotoruyu poluchaem znachenie $\tau$ . Obychno reshaetsya poryadka desyati takih sistem pri raznyh raskrytiyah diafragmy. Po shodimosti naidennyh znachenii $\tau$ mozhno sudit' ob uverennosti opredeleniya parametra nelineinosti. Metod diafragmirovaniya glavnogo zerkala v Tyan'-Shan'skoi observatorii vsegda byl osnovnym metodom opredeleniya $\tau$ pri nablyudeniyah na teleskopah AZT-14.

6.2.4 Metod poiska otklonenii ot puassonovskogo raspredeleniya.

Netradicionnyi metod opredeleniya $\tau$ byl vydvinut V.G.Kornilovym. Predstavim, chto my poluchili bol'shoe kolichestvo izmerenii postoyannogo svetovogo potoka. Effekt nelineinosti iskazhaet ne tol'ko izmerennuyu srednyuyu velichinu, no i drugie statisticheskie harakteristiki, v chastnosti dispersiyu. Dispersiya real'no registriruemogo chisla impul'sov svyazana s dispersiei dlya ideal'no lineinoi priemnoi apparatury sleduyushim sootnosheniem:

$\begin{displaymath} (\sigma_{N'})^2=\left({\frac{dN'}{dN}}\right)^2\,\sigma^2_N \end{displaymath}$

(6.10)

Podstavlyaya znachenie

iz vyrazheniya (3.6), differenciruya, i ispol'zuya svoistvo puassonovskogo processa $\sigma^2_N=N$ imeem

$\begin{displaymath} \sigma^2_{N'}= Ne^{-2\tau N}(1-\tau N)^2=N'e^{-\tau N}(1-\tau N) \end{displaymath}$

(6.11)

ili

$\begin{displaymath} p=\frac{\sigma^2_{N'}}{N'}=e^{-\tau N}(1-\tau N)\approx 1-3\tau N. \end{displaymath}$

(6.12)

Uravnenie (6.12) v sochetanii s uravneniem (3.11) reshaetsya chislenno odnim iz iteracionnyh metodov. Metod udoben, esli registraciya rezul'tatov izmerenii proizvoditsya s pomosh'yu EVM.

<< 6.1 Zhurnal nablyudenii | Oglavlenie | 6.3 Uchet atmosfernoi ekstinkcii >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce