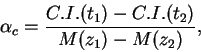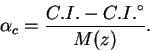<< 6.3 Uchet atmosfernoi ekstinkcii | Oglavlenie | 6.5 Metod pary >>
6.4 Metod Bugera
Esli odnu i tu zhe zvezdu pronablyudat' v monohromaticheskom
svete s dlinoi volny ![]() v dva momenta vremeni
v dva momenta vremeni ![]() i
i ![]() ,
sootvetstvenno pri vozdushnyh massah
,
sootvetstvenno pri vozdushnyh massah ![]() i
i ![]() , to raznost'
nablyudennyh zvezdnyh velichin, otnesennaya k raznosti
sootvetstvuyushih vozdushnyh mass, dast nam bugerovskii koefficient
atmosfernoi ekstinkcii
, to raznost'
nablyudennyh zvezdnyh velichin, otnesennaya k raznosti
sootvetstvuyushih vozdushnyh mass, dast nam bugerovskii koefficient
atmosfernoi ekstinkcii
Pered vami uravnenie pryamoi. Eto tak nazyvaemaya bugerovskaya pryamaya. Kogda zvezda sutochnym dvizheniem prohodit na nebesnoi sfere razlichnye vozdushnye massy, to zavisimost' velichiny oslableniya
Esli by atmosfernaya ekstinkciya vsegda byla postoyanna vo vremeni, to
metod byl by sovershenno idealen. No pri izmenenii atmosfernogo
poglosheniya metod mozhet privesti k grubym oshibkam. Predstavim dlya
opredelennosti, chto v techenie seansa nablyudenii ekstinkciya umen'shaetsya.
Eto dostatochno rasprostranennoe yavlenie. Ot vechera k glubokoi nochi
obychno ponizhaetsya temperatura, vymerzayut i osedayut visyashie v atmosfere
kapel'ki vody, osedaet dnevnaya pyl', podnyataya chelovecheskoi
deyatel'nost'yu, i t.p. S umen'sheniem koefficienta ekstinkcii
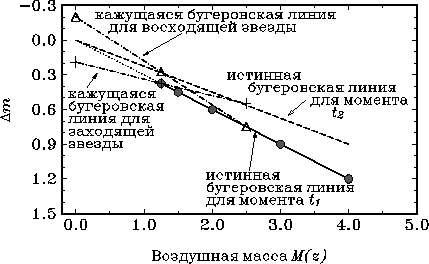
umen'shaetsya naklon bugerovskih linii. Poskol'ku vneatmosfernaya velichina
zvezdy ne zavisit ot yavlenii v atmosfere, vse eti linii dolzhny soitis'
v odnu tochku s koordinatami
![]() . Poskol'ku
vo vtoroi, tretii i posleduyushie momenty vremeni naklon bugerovskih
linii drugoi, to tochki prakticheski mogut okazat'sya na pryamoi, no
na drugoi, i ee ekstrapolyaciya k
. Poskol'ku
vo vtoroi, tretii i posleduyushie momenty vremeni naklon bugerovskih
linii drugoi, to tochki prakticheski mogut okazat'sya na pryamoi, no
na drugoi, i ee ekstrapolyaciya k ![]() dast nevernuyu vneatmosfernuyu
velichinu.
dast nevernuyu vneatmosfernuyu
velichinu.
Glavnyi nedostatok klassicheskogo metoda Bugera sostoit v tom, chto on ne rabotaet pri izmenyayusheisya ekstinkcii. A izmeneniya ekstinkcii tipichny. Na ravninnyh observatoriyah (v Moskve, v Krymu, v Pulkovo, v litovskoi observatorii bliz mestechka Moletai) redki nochi s ustoichivoi prozrachnost'yu. Ne vsegda oni byvayut i na vysokogornyh observatoriyah. V Tyan'-Shan'skoi observatorii GAISh sluchaetsya, chto zvezda, uzhe proshedshaya cherez meridian, prodolzhaet stanovit'sya yarche. V etih usloviyah luchshee, chto mozhno sdelat' metodom Bugera -- eto prokontrolirovat', bylo li izmenenie ekstinkcii ili ne bylo. Dlya etogo nablyudayut zvezdu, po kotoroi opredelyaetsya ekstinkciya, snachala do meridiana (zdes' zvezda voshodit, vozdushnaya massa umen'shaetsya, tochki polzut vverh po bugerovskoi linii), a zatem posle (zdes' zvezda zahodit, vozdushnaya massa uvelichivaetsya). Esli ekstinkciya ne izmenilas', tochki poidut obratno po toi zhe samoi pryamoi. K sozhaleniyu, tak byvaet redko. Po raznye storony meridiana tochki lozhatsya na pryamye s razlichnym naklonom, chto i harakterizuet izmenenie ekstinkcii. Iz etih dvuh naklonov inogda berut srednee ili prinimayut gipotezu, chto izmenenie koefficienta ekstinkcii proishodit lineino so vremenem, libo po kakomu-nibud' drugomu zakonu. No, kak pravilo, ekstinkciya menyaetsya dostatochno proizvol'no, i eti uhishreniya vse ravno ne privodyat k povysheniyu tochnosti.
Neredko zapisyvayut odnovremenno dve zvezdy: voshodyashuyu i zahodyashuyu, v nadezhde poluchit' srednyuyu bugerovskuyu pryamuyu za interval nablyudenii. Esli ekstinkciya izmenyalas' lineino so vremenem, to pri simmetrichnoi sheme nablyudenii est' shans poluchit' pravil'nuyu vneatmosfernuyu velichinu.
Formuly, analogichnye sootnosheniyam (6.18) i (6.19), mozhno
napisat' i dlya pokazatelei cveta. Po opredeleniyu
Iz nablyudenii zvezdy v dva momenta vremeni imeem
<< 6.3 Uchet atmosfernoi ekstinkcii | Oglavlenie | 6.5 Metod pary >>
|
Publikacii s klyuchevymi slovami:
Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
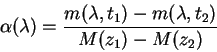
![\begin{displaymath}
C.I.= m(\lambda_1)-m(\lambda_2)=m_\circ(\lambda_1)-m_\circ(\...
...(\lambda_1)-\alpha(\lambda_2)]}_{\displaystyle\alpha_c}\,M(z),
\end{displaymath}](https://images.astronet.ru/pubd/2006/03/01/0001211924/img606.gif)