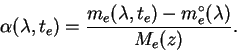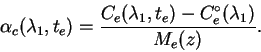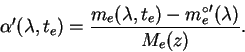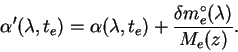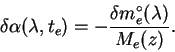Astronet > 6.6 Metod Nikonova

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 6.5 Metod pary | Oglavlenie | 6.7 Metod Sarycheva >>

6.6 Metod Nikonova (metod kontrol'nyh zvezd).

Metod V.B.Nikonova stal uzhe klassicheskim. On byl predlozhen eshe v sorokovyh godah. Vladimir Borisovich byl poistine pionerom otechestvennoi fotoelektricheskoi fotometrii, i hotya ego izmereniya 40-h i 50-h godov (kak i izmereniya vo vsem mire!) velis' v nestandartizovannyh fotometricheskih polosah i imeyut v nastoyashee vremya v osnovnom lish' istoricheskii interes, imenno v processe etih nablyudenii rodilsya znamenityi metod nezavisimogo opredeleniya izmenyayushihsya koefficientov ekstinkcii.

V metode Nikonova my dolzhny vybrat' i neodnokratno izmeryat' odnu zvezdu, kotoruyu budem nazyvat' ekstinkcionnoi (ili standartnoi), a takzhe izmeryat' programmnye zvezdy. I eto ponyatno! Ved' imenno izmereniya programmnyh zvezd sostavlyayut cel' lyubyh nablyudenii. Nasha zadacha ne tol'ko i ne stol'ko poluchit' koefficienty ekstinkcii, skol'ko opredelit' vneatmosfernye velichiny programmnyh zvezd.

Itak, v techenie nochi my mnogokratno izmeryaem ekstinkcionnuyu zvezdu i v promezhutkah mezhdu ee nablyudeniyami - programmnye zvezdy.

Esli izvestny tochnye znacheniya vneatmosfernoi zvezdnoi velichiny $m_e^\circ(\lambda)$ v monohromaticheskom svete s dlinoi volny $\lambda$ i pokazatelya cveta $C_e^\circ(\lambda_1)$ ekstinkcionnoi zvezdy v dannoi instrumental'noi fotometricheskoi sisteme (to est' raznost' monohromaticheskih zvezdnyh velichin dlya dlin voln $\lambda$ i $\lambda_1$ ), to, pronablyudav ee v moment vremeni , mozhno naiti dlya etogo momenta

$\begin{displaymath} \alpha(\lambda,t_e)=\frac{m_e(\lambda,t_e)-m^{\circ}_e(\lambda)}{M_e(z)}. \end{displaymath}$

(6.25)

$\begin{displaymath} \alpha_c(\lambda_1,t_e)=\frac{C_e(\lambda_1,t_e)-C^{\circ}_e(\lambda_1)} {M_e(z)}. \end{displaymath}$

(6.26)

Interpoliruya mezhdu znacheniyami $\alpha$ i $\alpha_c$ , poluchennymi v momenty

, i predpolagaya otsutstvie azimutal'nogo effekta, mozhem dlya lyubogo momenta naiti $\alpha(\lambda,t)$ i $\alpha_c(\lambda_1,t)$ i dalee

$\begin{displaymath} m_\circ(\lambda)=m(\lambda,t)-\alpha(\lambda,t)\,M(z), \end{displaymath}$

(6.27)

$\begin{displaymath} C_\circ(\lambda_1)=C(\lambda_1,t)-\alpha_c(\lambda_1,t)\,M(z). \end{displaymath}$

(6.28)

Pust' priblizhennoe znachenie zaatmosfernoi zvezdnoi velichiny ekstinkcionnoi zvezdy est' ${m_e^{\circ}}'(\lambda)$ . Ego mozhno poluchit', naprimer, proizvodya vynos za atmosferu so srednim dlya sezona znacheniem koefficienta ekstinkcii. Togda

(6.29)

gde $m_e^{\circ}(\lambda)$ - istinnaya vneatmosfernaya velichina ekstinkcionnoi zvezdy, a

- podlezhashaya opredeleniyu popravka.

Pronablyudav ekstinkcionnuyu zvezdu v ryad momentov vremeni i poluchiv nablyudennye znacheniya ee velichiny $m_e(\lambda,t_e)$ , nahodim predvaritel'nye znacheniya mgnovennyh koefficientov ekstinkcii

$\begin{displaymath} \alpha'(\lambda,t_e)=\frac{m_e(\lambda,t_e)-{m_e^\circ}'(\lambda)}{M_e(z)}. \end{displaymath}$

(6.30)

Podstavlyaya v uravnenie (6.30) formuly (6.25) i (6.29), imeem

$\begin{displaymath} \alpha'(\lambda,t_e)=\alpha(\lambda,t_e)+\frac{\delta m_e^\circ(\lambda)} {M_e(z)}. \end{displaymath}$

(6.31)

Itak, pogreshnost', vnesennaya v koefficient ekstinkcii pri ispol'zovanii znacheniya ${m_e^\circ}'(\lambda)$ , ravna

$\begin{displaymath} \delta\alpha(\lambda,t_e)=-\frac{\delta m_e^\circ(\lambda)}{M_e(z)}. \end{displaymath}$

(6.32)

Teper' privlechem na pomosh' programmnye zvezdy. Ochevidno, chto dlya zvezd postoyannogo bleska ih vneatmosfernye velichiny $m^\circ_{*}$ v raznye momenty vremeni $t_{*}$ postoyanny.

Izmerennye velichiny programmnyh zvezd $m_{*}$ vynosim za atmosferu s predvaritel'nymi (nepravil'nymi) koefficientami ekstinkcii $\alpha'$ prointerpolirovannymi na momenty ih nablyudenii $t_{*}$ .

$\begin{displaymath} {m_{*}^\circ}'(\lambda)=m_{*}(\lambda,t_{*})-\alpha'(\lambda,t_{*})\,M_{*}(z). \end{displaymath}$

(6.33)

Podstavlyaya (6.31) v (6.33), poluchaem

$\begin{displaymath} {m^\circ_{*}}'(\lambda)=m^\circ_{*}(\lambda)-\eta\,\delta m^\circ_e(\lambda), \end{displaymath}$

(6.34)

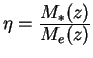gde $\eta=\frac{\displaystyle M_{*}(z)}{\displaystyle M_e(z)}$ na moment $t_{*}$ .

Provodya povtornye nablyudeniya programmnyh zvezd pri razlichnyh znacheniyah $\eta$ , mozhno naiti, reshaya sistemu uslovnyh uravnenii (6.34), neizvestnuyu popravku $\delta m^\circ_e(\lambda)$ , a sledovatel'no, soglasno (6.29) i tochnoe znachenie vneatmosfernoi velichiny ekstinkcionnoi zvezdy $m^\circ_e(\lambda)$ . Dlya pokazatelei cveta sovershenno analogichno

$\begin{displaymath} {C^\circ_{*}}'(\lambda_1)=C^\circ_{*}(\lambda_1,t)- \alpha'_c(\lambda_1,t-{*})\,M_{*}(z), \end{displaymath}$

(6.35)

$\begin{displaymath} {C^\circ_{*}}'(\lambda_1)=C^\circ_{*}(\lambda_1)- \eta\,\delta C^\circ_e(\lambda_1), \end{displaymath}$

(6.36)

gde $\delta C^\circ_e(\lambda_1)$ - podlezhashaya opredeleniyu popravka k predvaritel'nomu vneatmosfernomu pokazatelyu cveta ekstinkcionnoi zvezdy.

Chem bolee razlichayutsya znacheniya $\eta$ pri povtornyh nablyudeniyah, tem uverennee opredelyayutsya popravki $\delta m^\circ_e(\lambda)$ i $\delta C^\circ_e(\lambda_1)$ .

Teper', kogda opredeleny vneatmosfernye zvezdnye velichiny i pokazateli cveta ekstinkcionnoi zvezdy

$\begin{displaymath} m^\circ_e(\lambda)= {m^\circ_e}'(\lambda) + \delta m^\circ_e(\lambda), \end{displaymath}$

(6.37)

$\begin{displaymath} C^\circ_e(\lambda_1)= {C^\circ_e}'(\lambda_1) + \delta C^\circ_e(\lambda_1), \end{displaymath}$

(6.38)

vsyu obrabotku nablyudenii sleduet vesti po formulam (6.27), (6.28) s istinnymi koefficientami ekstinkcii, opredelyaemymi soglasno (6.25), (6.26).

Vsya hitrost' metoda sostoit v tom, chto Nikonov privlek dannye po programmnym zvezdam dlya opredeleniya popravki k koefficientu ekstinkcii na moment nablyudeniya ekstinkcionnoi zvezdy.

Nekotorye neudobstva mogut vozniknut' v dvuh sluchayah. Vo-pervyh, kogda sredi programmnyh zvezd mnogo peremennyh, zametno izmenyayushih svoi blesk v techenie seansa nablyudenii. Vo-vtoryh, kogda programmnye zvezdy nablyudayutsya nedaleko ot zenita i raznosti vozdushnyh mass $\Delta\eta$ pri povtornyh navedeniyah na kazhduyu iz nih blizki k nulyu.

Dlya isklyucheniya podobnyh neudobstv v 1976 g. Nikonov predlozhil modifikaciyu svoego metoda, kotoruyu nazval metodom kontrol'nyh zvezd. V etoi modifikacii rol' programmnyh zvezd igrayut special'no podobrannye kontrol'nye zvezdy, zavedomo neperemennye i udobno raspolozhennye na nebe. Kontrol'nye zvezdy nuzhny eshe i pri obrabotke nablyudenii v nemonohromaticheskih luchah (sm. p.6.9).

<< 6.5 Metod pary | Oglavlenie | 6.7 Metod Sarycheva >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce