Astronet > 6.8 Klassicheskii gamma-metod

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 6.7 Metod Sarycheva | Oglavlenie | 6.9

-modifikaciya metoda kontrol'nyh ... >>

6.8 Klassicheskii -metod

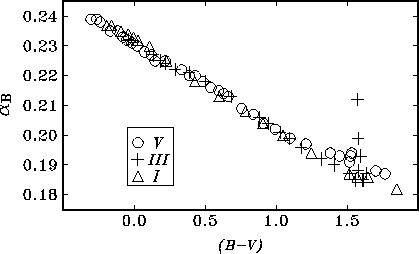
Rassmotrennye vyshe metody yavlyayutsya metodami, primenimymi dlya monohromaticheskogo izlucheniya. V sluchae geterohromnyh fotometricheskih polos sushestvuet zavisimost' bugerovskih koefficientov ekstinkcii ot raspredeleniya energii v spektre zvezdy i, kak sledstvie, ot ee pokazatelei cveta. Na ris.6.2 pokazana vychislennaya po formule (1.8) zavisimost' koefficienta atmosfernoi ekstinkcii $\alpha(B)$ v polose sistemy UBV ot pokazatelya cveta (B-V) zvezd razlichnyh spektral'nyh klassov pri prohozhdenii sveta ot nih cherez odnu atmosfernuyu massu dlya vysokogornoi observatorii. Vidno, chto dlya etogo sluchaya v shirokom intervale spektral'nyh klassov zavisimost' mozhno schitat' lineinoi; harakternyi razbros tochek okolo nee sostavlyaet neskol'ko tysyachnyh dolei zvezdnoi velichiny.

Ris. 6.2: Zavisimost' koefficienta atmosfernoi ekstinkcii $\alpha _B$ v polose

sistemy UBV ot pokazatelya cveta (B-V) dlya zvezd razlichnyh spektral'nyh tipov

$\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig6_2.eps}\end{center}\vspace{14pt} \end{figure}$

Pust' my pronablyudali v dannoi geterohromnoi polose dve standartnyh zvezdy s nomerami 1 i 2 i vneatmosfernymi pokazatelyami cveta $C^\circ_1$ i $C^\circ_2$ pri raznyh vozdushnyh massah i i poluchili izmerennye zvezdnye velichiny i . Etim izmereniyam budut sootvetstvovat' razlichnye koefficienty atmosfernoi ekstinkcii $\alpha(C^\circ_1)$ i $\alpha(C^\circ_2)$ . Vneatmosfernye velichiny obeih zvezd dlya etogo sluchaya budut ravny

$\begin{displaymath} m^\circ_1=m_1(z_1)-\alpha(C^\circ_1)\,M(z_1), \end{displaymath}$

(6.42)

$\begin{displaymath} m^\circ_2=m_2(z_2)-\alpha(C^\circ_2)\,M(z_2), \end{displaymath}$

(6.43)

Iz predpolozheniya o lineinosti zavisimosti $\alpha$ ot

sleduet

$\begin{displaymath} \alpha(C^\circ_2)=\alpha(C^\circ_1 )+\gamma\,(C^\circ_2-C^\circ_1), \end{displaymath}$

(6.44)

t.e. ekstinkcionnyi koefficient dlya vtoroi zvezdy raven ekstinkcionnomu koefficientu dlya pervoi zvezdy plyus popravka, proporcional'naya raznosti pokazatelei cveta etih zvezd. Poskol'ku istoricheski slozhilos' tak, chto v formule (6.44) koefficient proporcional'nosti prinyato oboznachat' bukvoi $\gamma$ , to metody ucheta atmosfernoi ekstinkcii, osnovannye na predpolozhenii o lineinoi zavisimosti koefficienta ekstinkcii ot pokazatelya cveta, chasto nazyvayut gamma-metodami.

Vychtem (6.43) iz (6.42) i podstavim tuda (6.44). Poluchim

$\begin{displaymath} \Delta m^\circ_{1-2}= m_1(z_1)-m_2(z_2)-\alpha(C^\circ_1)\Delta M(z)+ \gamma\,\Delta C^\circ\,M(z_2). \end{displaymath}$

(6.45)

V etom uravnenii velichina

poluchaetsya iz nablyudenii, izvestny $\Delta M(z)$ i

. Poskol'ku my imeem delo so standartami, izvestny $\Delta m^\circ_{1-2}$ i $\Delta C^\circ$ . Neizvestnymi yavlyayutsya $\alpha$ i $\gamma$ .

Pust' u nas imeyutsya na raznyh vozdushnyh massah dva standarta s odinakovymi pokazatelyami cveta. Dlya nih $\Delta C^\circ = 0$ . Sledovatel'no, chlen s $\gamma$ raven nulyu i mozhno opredelit' $\alpha(C^\circ_1)$ . Esli zhe my podberem dva standarta, otlichayushiesya po pokazatelyu cveta, i pronablyudaem ih na odinakovyh zenitnyh rasstoyaniyah, to est' pri $\Delta M(z)=0$ , chlen s $\alpha$ budet raven nulyu i mozhno budet opredelit' $\gamma$ .

Na praktike $\gamma$ -metod ne slishkom udoben, tak kak prihoditsya raspolagat' naborom standartov razlichnyh spektral'nyh klassov, chtoby udovletvorit' to trebovaniyu odinakovosti, to sil'nomu razlichiyu pokazatelei cveta. Oni dolzhny byt' raspolozheny na nebe tak, chtoby ih bylo legko nablyudat' na odinakovyh zenitnyh rasstoyaniyah. Vprochem, pri primenenii $\gamma$ -metoda obychno polagayut, chto koefficient $\gamma$ ne zavisit ni ot intervala spektral'nyh klassov, ni ot znacheniya $\alpha$ (to est' odinakov dlya vseh nochei). V etom sluchae $\gamma$ schitaetsya postoyannoi fotometricheskoi sistemy i opredelyayut etu velichinu redko: odin-dva raza v god.

$\gamma$ -metod, prakticheski v ego klassicheskoi interpretacii, shiroko primenyalsya i primenyaetsya v razlichnyh observatoriyah. Ego ispol'zovanie vpolne opravdano dlya fotometricheskih polos, raspolozhennyh v ``spokoinyh'' oblastyah funkcii raspredeleniya energii v spektre.

<< 6.7 Metod Sarycheva | Oglavlenie | 6.9

-modifikaciya metoda kontrol'nyh ... >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce