Astronet > 6.9 Gamma-modifikaciya metoda kontrol'nyh zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 6.8 Klassicheskii

-metod | Oglavlenie | 6.10 Metod Zdanavichyusa >>

6.9 Gamma-modifikaciya metoda kontrol'nyh zvezd

V klassicheskom -metode ne predusmotreny special'nye mery na sluchai raboty v usloviyah nochi s peremennoi ekstinkciei. Poetomu i v metode kontrol'nyh zvezd Nikonova, i v original'noi stat'e, izlagayushei metod Sarycheva, est' obobshenie na sluchai lineinoi zavisimosti koefficienta ekstinkcii ot pokazatelya cveta. Estestvenno, chto pri etom vychislitel'naya procedura sil'no uslozhnyaetsya. Rassmotrim takoe obobshenie na primere metoda kontrol'nyh zvezd.

Pust' imeyutsya lineinye sootnosheniya mezhdu koefficientami ekstinkcii $\alpha(t,C^\circ)$ i $\alpha_c(t,C^\circ)$ i raznost'yu vneatmosfernyh pokazatelei cveta $C^\circ$ i $C^\circ_e$ programmnoi i ekstinkcionnoi zvezd sootvetstvenno:

$\begin{displaymath} \alpha(t,C^\circ)=\alpha(t,C^\circ_e)+ \gamma\,(t,C^\circ_e)\,(C^\circ-C^\circ_e), \end{displaymath}$

(6.46)

$\begin{displaymath} \alpha_c(t,C^\circ)=\alpha_c(t,C^\circ_e)+ \gamma_c\,(t,C^\circ_e)\,(C^\circ-C^\circ_e), \end{displaymath}$

(6.47)

gde

$\begin{displaymath} \gamma(t,C^\circ_e)=\frac{d\alpha(t,C^\circ)}{dC}. \end{displaymath}$

(6.48)

$\begin{displaymath} \gamma_c(t,C^\circ_e)=\frac{d\alpha_c(t,C^\circ)}{dC}, \end{displaymath}$

(6.49)

Koefficienty $\gamma$ i $\gamma_c$ neveliki i obychno sostavlyayut neskol'ko sotyh, a takzhe neznachitel'no menyayutsya so vremenem.

Vliyanie effekta Forbsa mozhno priblizitel'no predstavit' v sleduyushem vide:

$\begin{displaymath} m^\circ=m(t)-[\alpha(t,C^\circ)+\varkappa(\alpha,C^\circ)\,M(z)]\,M(z), \end{displaymath}$

(6.50)

$\begin{displaymath} C^\circ=C(t)-[\alpha_c(t,C^\circ)+\varkappa_c(\alpha_c,C^\circ)\,M(z)]\,M(z), \end{displaymath}$

(6.51)

gde $\varkappa(\alpha,C^\circ)$ i $\varkappa_c(\alpha_c,C^\circ)$ - koefficienty, zavisyashie ot pokazatelya cveta i ekstinkcii. Nikonov rekomenduet vychislit' ih teoreticheski dlya ispol'zuemoi fotometricheskoi sistemy i predstavit' kak funkciyu pokazatelei cveta i koefficientov ekstinkcii.

Esli popravki $\varkappa(\alpha,C^\circ)\,M(z)^2$ i $\varkappa_c(\alpha_c,C^\circ)\,M(z)^2$ pridat' nablyudaemym znacheniyam zvezdnoi velichiny i pokazatelya cveta sootvetstvenno, to uravneniya (6.27) i (6.28) primut vid

$\begin{displaymath} m^\circ=[m(t)-\varkappa(\alpha,C^\circ)\,M^2(z)]-[\alpha(t,C^\circ) + \gamma(C^\circ -C^\circ_e)]\,M(z), \end{displaymath}$

(6.52)

$\begin{displaymath} C^\circ=[C(t)-\varkappa_c(\alpha_c,C^\circ)\,M^2(z)]-[\alpha_c(t,C^\circ) + \gamma_c(C^\circ -C^\circ_e)]\,M(z), \end{displaymath}$

(6.53)

chto formal'no vozvratit nas k uchetu ekstinkcii s koefficientami, lineino zavisyashimi ot pokazatelei cveta zvezd, i metody ucheta ekstinkcii, razrabotannye v etom predpolozhenii, sohranyat svoyu silu. Poetomu, budem schitat' spravedlivymi sootnosheniya

$\begin{displaymath} m^\circ=m(t)-[\alpha(t,C^\circ) + \gamma(C^\circ -C^\circ_e)]\,M(z) \end{displaymath}$

(6.54)

$\begin{displaymath} C^\circ=C(t)-[\alpha_c(t,C^\circ) + \gamma_c(C^\circ -C^\circ_e)]\,M(z). \end{displaymath}$

(6.55)

Nikonov ukazyvaet, chto dlya opredeleniya zvezdnoi velichiny i cveta ekstinkcionnoi zvezdy v metode kontrol'nyh zvezd mozhno polnost'yu ispol'zovat' monohromaticheskuyu metodiku, esli podobrat' kontrol'nye zvezdy s pokazatelyami cveta $C^\circ_k$ nastol'ko blizkimi k pokazatelyam cveta ekstinkcionnoi zvezdy $C^\circ_e$ , chtoby mozhno bylo prenebrech' popravkami $\gamma(C^\circ_k-C^\circ_e)\,M(z)$ i $\gamma_c(C^\circ_k-C^\circ_e)\,M(z)$ . Takie kontrol'nye zvezdy Nikonov nazyvaet kontrol'nymi zvezdami pervogo roda.

Dlya opredeleniya koefficientov $\gamma$ i $\gamma_c$ primenyayutsya kontrol'nye zvezdy vtorogo roda, t.e. sil'no otlichayushiesya po pokazatelyu cveta.

Dlya opredeleniya $\gamma_c$ snachala vynosim za atmosferu nablyudennye pokazateli cveta kontrol'nyh zvezd vtorogo roda , ispol'zuya dlya opredeleniya koefficienta ekstinkcii istinnoe znachenie pokazatelya cveta ekstinkcionnoi zvezdy $C^\circ_e$ , opredelennoe po kontrol'nym zvezdam pervogo roda. Takim obrazom nahodim priblizhennoe znachenie

$\begin{displaymath} {C^\circ_k}'=C_k(t_k)-\alpha_c(C^\circ_e,t_k)\,M(z), \end{displaymath}$

(6.56)

pri poluchenii kotorogo ne uchtena zavisimost' ekstinkcii ot pokazatelya cveta. Pribavlyaya i otnimaya v pravoi chasti (6.56) chlen $\gamma_c(C_k^{\circ}-C^\circ_e)\,M_k(z)$ i uchityvaya, chto

$\begin{displaymath} {C_k(t)} - {\alpha}_c(C_e^{\circ},t_k)\,M_k(z) - {\gamma}_c(C^{\circ}_k-C^{\circ}_e)\,M_k(z),=C^{\circ}_k \end{displaymath}$

a takzhe zamenyaya $(C^{\circ}_k-C^{\circ}_e)$ na $({C^{\circ}_k}'-C^{\circ}_e)$ , chto mozhno sdelat' vvidu malosti $\gamma$ (obychno $\gamma \le 0.03$ ), imeem

$\begin{displaymath} {C^{\circ}_k}'=C_k^{\circ}+({C^{\circ}_k}'-C^{\circ}_e)\,M_k(z)\,{\gamma}_c, \end{displaymath}$

(6.57)

Reshenie sistem uslovnyh uravnenii 6.57, sostavlennyh dlya kazhdoi kontrol'noi zvezdy, daet iskomye ${\gamma}_c$ i $C^{\circ}_k$ . Okonchatel'noe znachenie dlya ${\gamma}_c$ beretsya kak srednee vzveshennoe po vsem resheniyam (po vsem kontrol'nym zvezdam).

Dlya opredeleniya $\gamma$ neobhodimo reshit' analogichnuyu sistemu uslovnyh uravnenii:

$\begin{displaymath} {m^{\circ}_k}'=m_k^{\circ}+({C^{\circ}_k}'-C^{\circ}_e)\,M_k(z)\,{\gamma}, \end{displaymath}$

(6.58)

v kotoryh vse $C_k^{\circ}$ uzhe izvestny, a

$\begin{displaymath} {m^{\circ}_k}'=m_k(t)-{\alpha}({C^{\circ}_e},t_k)\,M_k(z), \end{displaymath}$

(6.59)

Analiz kontrol'nyh grafikov

$\begin{displaymath}[({C^{\circ}_k}'-C^{\circ}_k);({C^{\circ}_k}'-C^{\circ}_k)\,M_k(z)]\end{displaymath}$

$\begin{displaymath}[({m^{\circ}_k}'-m^{\circ}_k);({C^{\circ}_k}'-C^{\circ}_k)\,M_k(z)],\end{displaymath}$

poluchaemyh v processe vypolneniya tekushei programmy, pozvolyaet naiti srednie znacheniya koefficientov $\gamma_c$ i $\gamma$ dlya razlichnyh sezonov, a takzhe ocenit' velichinu ih fluktuacii.

Esli vse zhe budet priznano, chto neobhodimo poluchat' mgnovennye znacheniya koefficientov $\gamma_c$ i $\gamma$ , to eto potrebuet nablyudenii vtoroi ekstinkcionnoi zvezdy, s pokazatelem cveta, rezko otlichayushimsya ot osnovnoi. Nablyudeniya dvuh ekstinkcionnyh zvezd ``1'' i ``2'' s pokazatelyami cveta $C^{\circ}_{e,1}$ i $C^{\circ}_{e,2}$ i pozvolyayut stroit' grafiki nochnogo hoda ekstinkcii

$\begin{displaymath} [\alpha_c(C^{\circ}_{e,1},t)~i~\alpha_c(C^{\circ}_{e,2},t) =... ...irc}_{e,1},t)+\gamma_c(t)(C^{\circ}_{e,2}-C^{\circ}_{e,1}),\\ \end{displaymath}$

$\begin{displaymath} [\alpha(C^{\circ}_{e,1},t)~i~\alpha(C^{\circ}_{e,2},t) = \al... ...irc}_{e,1},t)+\gamma_c(t)(C^{\circ}_{e,2}-C^{\circ}_{e,1}),\\ \end{displaymath}$

S etih grafikov snimayutsya znacheniya $\gamma_c(t)$ i $\gamma(t)$ dlya ryada momentov vremeni

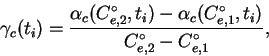
$\begin{displaymath} \gamma_c(t_i) = \frac{\alpha_c(C^{\circ}_{e,2},t_i)-\alpha_c(C^{\circ}_{e,1},t_i)} {C^{\circ}_{e,2} -C^{\circ}_{e,1}}, \end{displaymath}$

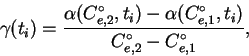
$\begin{displaymath} \gamma(t_i) = \frac{\alpha(C^{\circ}_{e,2},t_i)-\alpha(C^{\circ}_{e,1},t_i)} {C^{\circ}_{e,2} -C^{\circ}_{e,1}}, \end{displaymath}$

i stroitsya ih hod v techenie nochi.

<< 6.8 Klassicheskii

-metod | Oglavlenie | 6.10 Metod Zdanavichyusa >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce