Astronet > 6.10 Metod Zdanavichyusa

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Precizionnaya fotometriya

<< 6.9 Gamma-modifikaciya metoda ... | Oglavlenie | 6.11 Metodika Tyan'-Shan'skoi obs... >>

6.10 Metod Zdanavichyusa dlya pokazatelei cveta

Kak my ubedilis', geterohromnyi variant metoda kontrol'nyh zvezd Nikonova, gromozdok i ne svoboden ot uproshenii, v primenimosti kotoryh eshe nuzhno ubezhdat'sya. I eto tol'ko dlya prosteishego sluchaya lineinoi zavisimosti koefficientov ekstinkcii ot pokazatelei cveta. V obshem zhe sluchae takoi zavisimosti net!

Ris. 6.3: Zavisimost' koefficienta atmosfernoi ekstinkcii $\alpha _U$ v polose

sistemy UBV ot pokazatelya cveta (B-V) dlya zvezd razlichnyh spektral'nyh tipov

$\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig6_3.eps}\end{center}\end{figure}$

Eto ubeditel'no pokazyvaet grafik na ris.6.3. Kak i na ris. 6.2, eto ne neposredstvennye dannye nablyudenii, a rezul'tat vychislenii osnovnogo integrala. Vidno, chto dlya vseh klassov svetimosti net ne tol'ko lineinosti, no i monotonnosti hoda krivoi. Zavisimosti razlichny dlya raznyh klassov svetimosti. Pri pokazatele cveta

primenenie dlya zvezd-sverhgigantov koefficienta ekstinkcii, poluchennogo po zvezdam-karlikam, privedet k oshibke okolo 5na kazhduyu edinicu atmosfernoi massy. Otmetim, chto kachestvenno vid etogo grafika takoi zhe, kak i dvuhcvetnoi diagrammy

. Prichinoi nemonotonnosti yavlyaetsya vozniknovenie i, zatem, ischeznovenie bal'merovskogo skachka po mere izmeneniya poverhnostnoi temperatury zvezd so spektral'nym klassom. Nikakie lineinye uprosheniya zdes' uzhe ne pomogut. Nuzhno primenyat' principial'no drugie metody. Po-vidimomu pervym, kto sozdal i primenil posledovatel'no-geterohromnyi metod ucheta atmosfernoi ekstinkcii, byl K.Zdanavichyus. On razrabatyval metod vynosa za atmosferu pokazatelei cveta srednepolosnoi Vil'nyusskoi sistemy, no s uspehom primenil ego i dlya shirokopolosnyh sistem.

V metode Zdanavichyusa dlya kazhdogo konkretnogo nabora krivyh reakcii delaetsya special'nyi raschet. Rassmotrim etot metod na primere pokazatelei cveta shirokopolosnoi sistemy .

Pri raschetah Zdanavichyus podstavlyal v osnovnuyu geterohromnuyu formulu (1.8) krivye reakcii fotometricheskoi sistemy $T_i(\lambda)$ , nekotoruyu krivuyu $p(\lambda)$ , harakterizuyushuyu pogloshenie v standartnoi atmosfere i normal'nye raspredeleniya energii v spektrah zvezd raznyh spektral'nyh tipov $E(\lambda )$ , vidoizmenyaya ih v raznoi stepeni v sootvetstvii s zakonom mezhzvezdnogo pokrasneniya. Funkciya $p(\lambda)$ predstavlyaet nekotoruyu srednyuyu atmosferu, a ne real'nuyu atmosferu v moment nablyudenii. Odnako, poskol'ku metod razrabatyvalsya tol'ko dlya vynosa pokazatelei cveta, Zdanavichyus schel vozmozhnym prenebrech' otkloneniyami real'noi atmosfery ot standartnoi modeli, schitaya, chto variacii ekstinkcii neselektivny.

Rassmotrim snachala samyi slozhnyi sluchai vynosa pokazatelya cveta .

Pust' $C^{\circ}_{U-B}$ -- vneatmosfernyi pokazatel' cveta zvezdy, a $C_{U-B}(z)$ -- izmerennyi pokazatel' cveta pod atmosferoi pri zenitnom rasstoyanii . Raznost' etih pokazatelei, to est' velichinu vynosa, Zdanavichus predstavlyaet v vide

$\begin{displaymath} C_{U-B}(z) - C^{\circ}_{U-B} = {\alpha}_{UB}'\,M(z) + r_{UB}[M(z)]^2. \end{displaymath}$

(6.60)

Zdes' ${\alpha}_{UB}'$ -- neizvestnyi koefficient ekstinkcii, a $r_{UB}$ -- koefficient Forbsa, kotoryi uchityvaet nelineinost' zavisimosti koefficienta ekstinkcii ot vozdushnoi massy. Effekt Forbsa yavno sushestven dlya ul'trafioletovoi polosy, tak kak tut samyi krutoi naklon zavisimosti koefficientov ekstinkcii ot dliny volny, iz-za krutizny releevskoi funkcii i funkcii poglosheniya ozonom. Koefficient $r_{UB}$ , v svoyu ochered', zavisit ot spektral'nogo klassa, mezhzvezdnogo poglosheniya i ot zakona atmosfernoi ekstinkcii. Zdanavichyus prishel k vyvodu, chto vse eti zavisimosti priblizhenno uchityvayutsya formuloi

$\begin{displaymath} r_{UB} = -0.028{\alpha}_{UB}' , \end{displaymath}$

(6.61)

sledovatel'no,

$\begin{displaymath} {\alpha}_{UB}' = \frac{C_{U-B}(z) - C^{\circ}_{U-B}} {M(z)\,[1-0.028\,M(z)]} . \end{displaymath}$

(6.62)

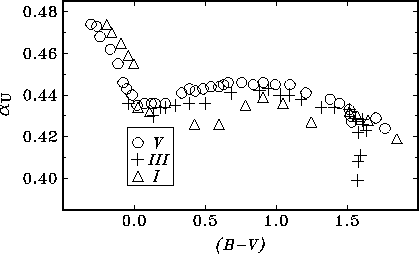
Raschety po integral'noi formule, s pomosh'yu kotoryh mozhno postroit' grafiki tipa pokazannogo na ris.6.3, pozvolyayut opredelit' naklon linii narastayushego poglosheniya. Zdanavichyus stroil grafiki $\alpha_{UB}$ ,(U-B) i $\alpha_{UB}$ ,(B-V). Na oboih grafikah uglovoi koefficient etih linii okazalsya odinakovym i ravnym .

Posle etogo byli sformirovany nezavisimye ot mezhzvezdnogo poglosheniya koefficienty

$\begin{displaymath} {\varkappa}_{UB}' = {\alpha}_{UB}' + 0.012(U-B) \end{displaymath}$

(6.63)

$\begin{displaymath} {{\varkappa}_{UB}^{BV}}' = {{\alpha}_{UB}}' + 0.012(B-V) \end{displaymath}$

(6.64)

Zdanavichyus obnaruzhil, chto pri vsei slozhnosti vida zavisimostei koefficientov $\varkappa_{UB}$ ot (U-B),(B-V) i $Q_{UBV}$ , eti koefficienty udovletvoritel'no vyrazhaetsya kombinaciei dvuh parametrov :

$\begin{displaymath} {\varkappa}_{UB} = 0.37 - 0.067\,Q_{UBV} + 0.073\,Q_{BVR}, \end{displaymath}$

(6.65)

$\begin{displaymath} {{\varkappa}_{UB}^{BV}}' = 0.36 - 0.078\,Q_{UBV} + 0.069\,Q_{BVR}, \end{displaymath}$

(6.66)

Vychislennye po formulam (6.65) i (6.66) koefficienty ekstinkcii otlichayutsya ot deistvitel'nyh ne bolee chem na 0.02. V etih formulah neyavno zaklyuchena zavisimost' $\alpha_{UB}$ ot spektral'nogo klassa i klassa svetimosti, vyrazhennaya cherez parametry . Podcherknem vazhnost' polosy . Bez parametra $Q_{BVR}$ ne udalos' by approksimirovat' koefficienty nikakoi lineinoi formuloi. Dlya pokazatelya cveta delo obstoit mnogo proshe, tak kak izmenenie $\varkappa_{BV}$ ot spektral'nogo klassa zvezdy horosho uchityvaetsya formuloi

$\begin{displaymath} \varkappa_{BV} = 0.18 - 0.05\,Q_{BVR}. \end{displaymath}$

(6.67)

Dlya pokazatelya cveta

Zdanavichyus primenyaet klassicheskii $\gamma$ -metod. Znachenie $\gamma=0.0105$ i

$\begin{displaymath} \alpha_{VR} = \alpha_{VR}(A0V) + 0.0105\,(V-R) . \end{displaymath}$

(6.68)

Dlya kakoi-libo drugoi fotometricheskoi sistemy, naprimer dlya polos WBVR, mozhno takim zhe priemom poluchit' svoi koefficienty. Naprimer, formula, analogichnaya sootnosheniyu (6.66) takova:

(6.69)

Zametim, chto znacheniya chislovyh koefficientov pri v formule (6.69) primerno v 2-3 raza menee takovyh v formule (6.66). Sledovatel'no, v sisteme WBVR oshibki opredeleniya parametrov budut slabee vliyat' na oshibki vynosa, chem v sisteme .

<< 6.9 Gamma-modifikaciya metoda ... | Oglavlenie | 6.11 Metodika Tyan'-Shan'skoi obs... >>

Publikacii s klyuchevymi slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie Publikacii so slovami: Fotometricheskaya sistema - zvezdnaya velichina - fotometriya - spektrofotometriya - atmosfernoe pogloshenie
Sm. takzhe: Zvezdnye velichiny Zahodyashaya ten' Zemli Spektral'noe i fotometricheskoe issledovanie linzovidnoi galaktiki s obolochkami NGC 474 Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Laboratoriya spektroskopii zvezd SAO RAN Laboratoriya spektroskopii i fotometrii vnegalakticheskih ob'ektov SAO RAN Pokazatel' cveta Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce