Astronet > 1.7 Variacionnyi princip

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 1.6 Osnovy termodinamiki zvezd | Oglavlenie | 1.8 Teorema viriala >>

1.7 Variacionnyi princip

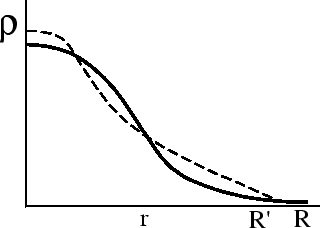
$\begin{wrapfigure}{l}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f10.ai}\hss} \end{wrapfigure}$

Ris. 10.

V himicheski odnorodnoi zvezde neobyazatel'no perenosit' veshestvo: k tem zhe rezul'tatam otnositel'no ustoichivosti mozhno priiti, prosto izmenyaya raspredelenie veshestva $\rho (r)$ , ne menyaya pri etom vzaimnogo raspolozheniya sloev (ris. 10). Mozhno utverzhdat', chto esli ravnovesie zvezdy slegka narushit', to energiya pri etom ne izmenitsya. Tochnaya formulirovka etogo utverzhdeniya: uslovie ekstremuma polnoi energii zvezdy ${\cal{E}}$ sovpadaet s usloviem ravnovesiya.

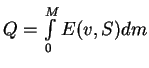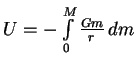Rassmatrivaem zvezdu s proizvol'nym raspredeleniem entropii . Polnaya energiya zvezdy ${\cal{E}}$ skladyvaetsya iz teplovoi energii $Q=\int\limits_0^M E(v,S) dm$ i gravitacionnoi energii^1.2 $U=-\int\limits_0^M {Gm\over r}\,dm$ :

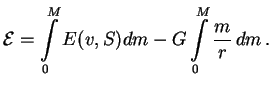
$\displaystyle {\cal{E}}=\int\limits_0^M E(v,S) dm-G\int\limits_0^M {m\over r}\,dm\,.$

Naidem uslovie ekstremuma ${\cal{E}}$ , ispol'zuya

v kachestve lagranzhevoi koordinaty. Raspredelenie plotnosti polnost'yu opredeleno, esli zadana funkciya $\rho (m)$ . Budem var'irovat'

, t.e. smeshat' otdel'nye sloi, schitaya entropiyu

fiksirovannoi, pri etom u nas budut opredeleny variacii i vseh ostal'nyh velichin. Imeem:

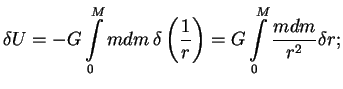
$\displaystyle \delta U=-G\int\limits_0^M mdm \,\delta \left({1\over r}\right)=G\int\limits_0^M {mdm\over r^2} \delta r;$

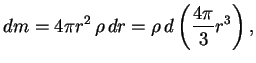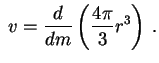
$\displaystyle dm=4\pi r^2 \,\rho \,dr=\rho \,d\left({4\pi \over 3}r^3\right),$ poetomu $\displaystyle \;v={d\over dm}\left({4\pi \over 3}r^3\right)\,.$

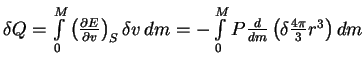Togda $\delta Q=\int\limits_0^M \left({\partial E\over \partial v}\right)_S \delta v \,dm=-\int\limits_0^M P{d\over dm}\left(\delta {4\pi\over 3}r^3\right)dm$ . Integriruya po chastyam s uchetom togo, chto $r(0)=0, \;P(M)=0,$ poluchim

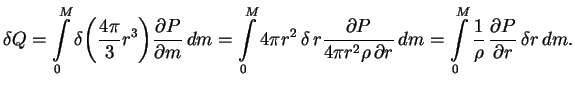
$\displaystyle \delta Q=\int\limits_0^M \delta {\left({4\pi \over 3}r^3\right)}{... ...=\int\limits_0^M {1\over \rho} \,{\partial P \over \partial r} \,\delta r\,dm.$

V rezul'tate

$\displaystyle \delta {\cal{E}}=\int\limits_0^M dm \,\left[{1\over \rho} \,{\partial P \over \partial r} +{Gm\over r^2}\right] \,\delta \,r.$

Esli ${\cal{E}}$ ekstremal'no, to $\delta {\cal{E}}=0$ pri lyubyh $\delta \, r(m)$ , sledovatel'no, iz ekstremal'nosti ${\cal{E}}$ sleduet uravnenie ravnovesiya

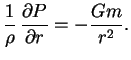
$\displaystyle {1\over \rho} \,{\partial P \over \partial r}=-{Gm\over r^2}.$

Chem polezen variacionnyi princip? Okazyvaetsya, chto s pomosh'yu etogo principa issledovat' ustoichivost' mnogo proshe, chem ispol'zuya uravnenie ravnovesiya. V etom mozhno ubedit'sya sleduyushim obrazom. Zapishem vyrazhenie dlya polnoi energii zvezdy, ne predpolagaya ravenstva nulyu skorostei dvizheniya veshestva zvezdy:

$\displaystyle {\cal{E}}=\int\limits_0^M \left[E(v,S)-{Gm\over r}+{u^2\over 2}\right] \,dm,$

gde

-- skorost' elementa massy. Ochevidno, chto ravnovesnoe rasstoyanie (kotoroe vsegda sootvetstvuet ekstremumu energii) budet ustoichivym, esli ekstremum yavlyaetsya minimumom. Deistvitel'no, togda iz nego ne mozhet vozniknut' nikakoe drugoe sostoyanie, ni s

(no drugim

), ni tem bolee s

. Sledovatel'no, issledovanie ustoichivosti svoditsya k nahozhdeniyu uslovii, pri kotoryh vtoraya variaciya energii $\delta^2 {\cal{E}}>0$ .

Pomimo issledovaniya ustoichivosti variacionnyi princip pozvolyaet nahodit' priblizhennye resheniya dlya struktury zvezdy.

<< 1.6 Osnovy termodinamiki zvezd | Oglavlenie | 1.8 Teorema viriala >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce