<< 1.7 Variacionnyi princip | Oglavlenie | 2. Analiticheskaya teoriya politropnyh ... >>
1.8 Teorema viriala
Predpolozhim, chto uravnenie sostoyaniya stepennoe:
![]() . Togda udel'naya
teplovaya energiya
. Togda udel'naya
teplovaya energiya
![]() . My znaem, chto v ravnovesii
. My znaem, chto v ravnovesii
![]() pri proizvol'noi
pri proizvol'noi
![]() . Pust'
. Pust'
![]() .
Takoe vozmushenie
opisyvaet podobnoe (gomologicheskoe) rasshirenie ili szhatie zvezdy. Togda
.
Takoe vozmushenie
opisyvaet podobnoe (gomologicheskoe) rasshirenie ili szhatie zvezdy. Togda
![]() . Sledovatel'no,
. Sledovatel'no,
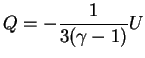
Teper' polozhim
![]() , prichem ne budem schitat'
, prichem ne budem schitat' ![]() maloi velichinoi,
a ishodnoe sostoyanie -- ravnovesnym. Oboznachim cherez
maloi velichinoi,
a ishodnoe sostoyanie -- ravnovesnym. Oboznachim cherez ![]() i
i ![]() sootvetstvuyushie
velichiny energii ishodnoi modeli. Togda posle preobrazovaniya
sootvetstvuyushie
velichiny energii ishodnoi modeli. Togda posle preobrazovaniya
![]() (dlya stepennogo uravneniya sostoyaniya). Esli
(dlya stepennogo uravneniya sostoyaniya). Esli
![]() , to
, to
![]() . Kak vyglyadit v etom sluchae
krivaya
. Kak vyglyadit v etom sluchae
krivaya
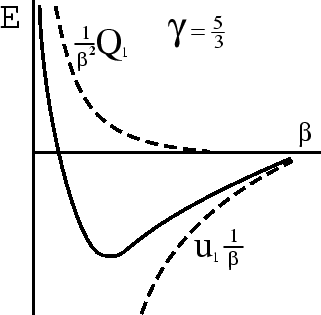
![]() ? Pri
? Pri
![]() asimptotika opredelyaetsya
velichinoi
asimptotika opredelyaetsya
velichinoi ![]() , pri
, pri
![]() -- velichinoi
-- velichinoi ![]() (ris. 11). Poluchaem, chto pri
(ris. 11). Poluchaem, chto pri
![]() krivaya imeet odin i tol'ko odin minimum, t.e. ravnovesie ustoichivo.
krivaya imeet odin i tol'ko odin minimum, t.e. ravnovesie ustoichivo.
Poluchim teoremu viriala drugim sposobom iz uravneniya ravnovesiya, prichem zavisimost'
![]() mozhet byt' proizvol'noi. (Vyshe pri vyvode teoremy viriala iz variacionnogo
principa zavisimost'
mozhet byt' proizvol'noi. (Vyshe pri vyvode teoremy viriala iz variacionnogo
principa zavisimost'
![]() byla sushestvenna). Umnozhim uravnenie ravnovesiya
(1.6) na
byla sushestvenna). Umnozhim uravnenie ravnovesiya
(1.6) na ![]() :
:
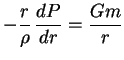
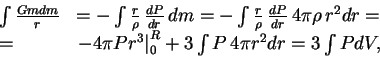
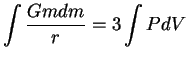
Pri stepennom uravnenii sostoyaniya, ispol'zuya
![]() , imeem uzhe
izvestnoe sootnoshenie
, imeem uzhe
izvestnoe sootnoshenie
![]() .
.
V deistvitel'nosti uravnenie sostoyaniya ne stepennoe, no dlya mnogih ocenok polezno
znat' svoistva zvezd s takim uravneniem sostoyaniya. Dlya stepennogo uravneniya
sostoyaniya imeetsya podobie, t.e. dostatochno reshit' zadachu pri dannom ![]() dlya odnogo znacheniya
dlya odnogo znacheniya ![]() , chtoby naiti funkcional'nuyu zavisimost'
, chtoby naiti funkcional'nuyu zavisimost' ![]() i
i ![]() . V sistemu uravnenii
. V sistemu uravnenii
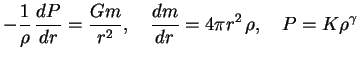
![$\displaystyle [G]={\mbox{sm}^3\over \mbox{g} \cdot \mbox{s}^2}, \;[K]={\mbox{sm...
...\over \mbox{sm}^3}\right)^{-\gamma+1}, \;[\rho_c]=
{\mbox{g}\over\mbox{sm}^3}.
$](http://images.astronet.ru/pubd/2008/02/15/0001226214/img305.gif)
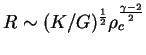 .
.
Bolee naglyadno eta svyaz' poluchaetsya s pomosh'yu poryadkovyh ocenok:
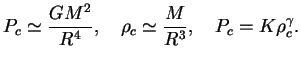
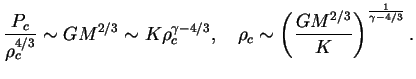
Podcherknem, chto vid krivyh ![]() i
i ![]() zavisit ot bezrazmernoi
velichiny
zavisit ot bezrazmernoi
velichiny ![]() , t.e. krivye dlya raznyh
, t.e. krivye dlya raznyh ![]() ne podobny.
ne podobny.
<< 1.7 Variacionnyi princip | Oglavlenie | 2. Analiticheskaya teoriya politropnyh ... >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |