<< 1.8 Teorema viriala | Oglavlenie | 2.2 Osnovnye parametry politropy >>
2. Analiticheskaya teoriya politropnyh sharov (teoriya Leina-Rittera-Emdena)
Razdely
- 2.1 Uravnenie Emdena
- 2.2 Osnovnye parametry politropy
- 2.3 Chastnye sluchai politropnyh modelei
- 2.4 Teoriya belyh karlikov
- 2.5 Goryachie zvezdy
2.1 Uravnenie Emdena
V etoi glave my budem izuchat' ravnovesnye konfiguracii zvezd, podchinyayushihsya stepennomu (politropnomu) uravneniyu sostoyaniya
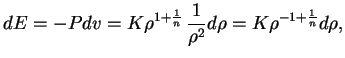
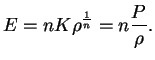
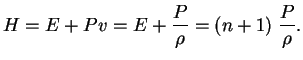
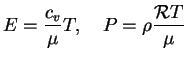 ili
ili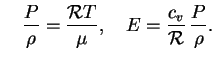
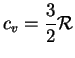 i
i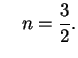
To zhe mozhno vychislit' i dlya mnogoatomnyh gazov, no etot sluchai neinteresen: seichas my znaem o zvezdah neskol'ko bol'she, chem 100 let nazad.
Vvedem peremennuyu ![]() takim obrazom, chtoby
takim obrazom, chtoby
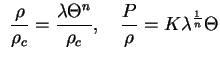 i
i
Budem uproshat' poluchennoe sootnoshenie, izmenyaya masshtab, t.e. vvodya peremennuyu
![]() cherez sootnoshenie
cherez sootnoshenie
![]() ,
,
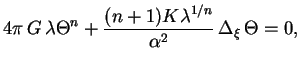
Vyberem ![]() tak, chtoby
tak, chtoby
![]() .
Togda uravnenie ravnovesiya zapishetsya v vide
.
Togda uravnenie ravnovesiya zapishetsya v vide
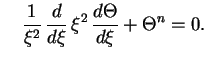
Takim obrazom, pri dannom ![]() uravnenie ravnovesiya odno i to zhe dlya zvezd lyuboi
massy. Reshaya uravnenie pri granichnyh usloviyah
uravnenie ravnovesiya odno i to zhe dlya zvezd lyuboi
massy. Reshaya uravnenie pri granichnyh usloviyah
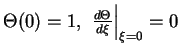 (t.e. polozhiv
(t.e. polozhiv
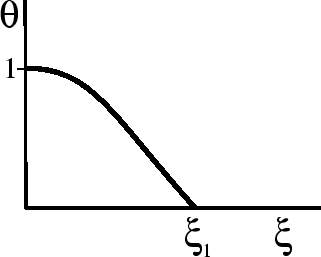
![]() ), poluchim monotonnoe
ubyvanie
), poluchim monotonnoe
ubyvanie ![]() ot edinicy k nulyu
(ris. 12). Znachenie
ot edinicy k nulyu
(ris. 12). Znachenie ![]() , gde
, gde
![]() , yavlyaetsya granicei zvezdy. Plotnost'
, yavlyaetsya granicei zvezdy. Plotnost' ![]() , proporcional'naya
, proporcional'naya ![]() , pri
, pri
![]() spadaet bolee kruto, chem
spadaet bolee kruto, chem ![]() . My uzhe pokazyvali v
razdele 1.5, chto pri
stepennom uravnenii sostoyaniya na krayu zvezdy
. My uzhe pokazyvali v
razdele 1.5, chto pri
stepennom uravnenii sostoyaniya na krayu zvezdy
![]() .
No
.
No
![]() , t.e.
, t.e.
![]() . Poetomu
. Poetomu
![]() i vblizi
i vblizi ![]() velichina
velichina ![]() prohodit nul' s konechnoi
proizvodnoi, hotya
prohodit nul' s konechnoi
proizvodnoi, hotya ![]() ``steletsya'' (pri
``steletsya'' (pri ![]() ), t.e. podhodit k nulyu, kasayas'
osi absciss.
), t.e. podhodit k nulyu, kasayas'
osi absciss.
Yasno, chto dlya zvezd s razlichnymi ![]() i
i ![]() krivye s odinakovymi
krivye s odinakovymi ![]() podobny.
Dostatochno znat' tol'ko odnu funkciyu
podobny.
Dostatochno znat' tol'ko odnu funkciyu
![]() . Podcherknem vazhnost'
granichnogo
usloviya
. Podcherknem vazhnost'
granichnogo
usloviya
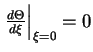 . Obratnoe
. Obratnoe
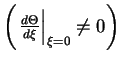 oznachalo by konechnyi skachok
uskoreniya v centre (t.e. osobennost')2.1.
oznachalo by konechnyi skachok
uskoreniya v centre (t.e. osobennost')2.1.
Neskol'ko avtorov v proshlom veke chislenno prointegrirovali uravnenie dlya razlichnyh
![]() . V chastnosti, Emden poluchil tablicy
. V chastnosti, Emden poluchil tablicy
![]() c bol'shoi tochnost'yu.
Znachenie etih vychislenii teper' neveliko, tak kak raschet real'nyh zvezd provoditsya
s uchetom fizicheskih faktorov, sovershenno ne uchityvaemyh v politropnoi teorii
(nestepennoe uravnenie sostoyaniya; istinnaya svyaz'
c bol'shoi tochnost'yu.
Znachenie etih vychislenii teper' neveliko, tak kak raschet real'nyh zvezd provoditsya
s uchetom fizicheskih faktorov, sovershenno ne uchityvaemyh v politropnoi teorii
(nestepennoe uravnenie sostoyaniya; istinnaya svyaz' ![]() i
i ![]() poluchaetsya iz
rassmotreniya vseh processov, vklyuchaya perenos izlucheniya, yadernye reakcii). Odnako
dlya kachestvennyh issledovanii reshenie uravnenii Emdena ves'ma polezno. Naprimer,
s pomosh'yu politropnoi modeli legko pokazat' nevozmozhnost' sushestvovaniya
sverhmassivnyh zvezd. Eto vazhno dlya problemy kvazarov.
poluchaetsya iz
rassmotreniya vseh processov, vklyuchaya perenos izlucheniya, yadernye reakcii). Odnako
dlya kachestvennyh issledovanii reshenie uravnenii Emdena ves'ma polezno. Naprimer,
s pomosh'yu politropnoi modeli legko pokazat' nevozmozhnost' sushestvovaniya
sverhmassivnyh zvezd. Eto vazhno dlya problemy kvazarov.
<< 2. Politropnye shary | Oglavlenie | 2.2 Osnovnye parametry politropy >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |