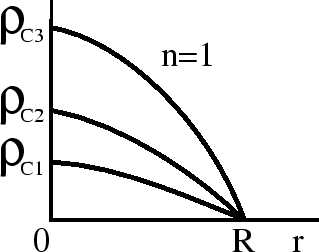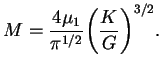<< 2.2 Osnovnye parametry politropy | Oglavlenie | 2.4 Teoriya belyh karlikov >>
2.3 Chastnye sluchai politropnyh modelei
1. ![]() . Kak vidno iz vyshe privedennoi tablicy, pri
. Kak vidno iz vyshe privedennoi tablicy, pri ![]() bezrazmernyi radius
bezrazmernyi radius
![]() . Iz formul dlya
. Iz formul dlya
![]() vidno, chto konechnye
znacheniya energii zvezdy sovmestimy s konechnoi massoi tol'ko pri
vidno, chto konechnye
znacheniya energii zvezdy sovmestimy s konechnoi massoi tol'ko pri
![]() .
Resheniya uravneniya Emdena s
.
Resheniya uravneniya Emdena s ![]() voobshe teryayut obychnyi fizicheskii smysl.
voobshe teryayut obychnyi fizicheskii smysl.
Sluchai ![]() imeet analiticheskoe reshenie vida
imeet analiticheskoe reshenie vida
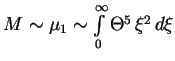 shoditsya na verhnem predele. Polnyi moment inercii
shoditsya na verhnem predele. Polnyi moment inercii
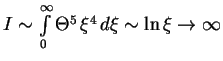 , no
, no
2. ![]() . Dlya davleniya v etom sluchae imeet mesto sootnoshenie
. Dlya davleniya v etom sluchae imeet mesto sootnoshenie
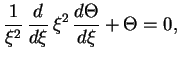
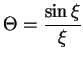
i obrashaetsya v nul' pri ![]() . V silu lineinosti zadachi radius zvezdy
. V silu lineinosti zadachi radius zvezdy ![]() ne zavisit ot massy. Pri dannom
ne zavisit ot massy. Pri dannom ![]() velichiny
velichiny ![]() i
i ![]() proporcional'ny
proporcional'ny ![]() ,
i v odin ob'em mozhno vlozhit' (ravnovesno!) raznoe kolichestvo veshestva. Pri
uvelichenii massy rastet tol'ko central'naya plotnost'
,
i v odin ob'em mozhno vlozhit' (ravnovesno!) raznoe kolichestvo veshestva. Pri
uvelichenii massy rastet tol'ko central'naya plotnost' ![]() (ris. 13).
(ris. 13).
Zadacha. Poluchite etot rezul'tat iz razmernostnyh soobrazhenii. Uchtite
pri etom, chto razmernost' ![]() zavisit ot indeksa
zavisit ot indeksa ![]() .
.
3. ![]() -- neszhimaemaya zhidkost'. Formal'no pri
-- neszhimaemaya zhidkost'. Formal'no pri ![]() iz uravneniya sostoyaniya
iz uravneniya sostoyaniya
![]() sleduet, chto malye izmeneniya
sleduet, chto malye izmeneniya ![]() dayut bol'shie izmeneniya
dayut bol'shie izmeneniya ![]() .
Eto daet nam pravo otozhdestvlyat' sluchai
.
Eto daet nam pravo otozhdestvlyat' sluchai ![]() s neszhimaemoi odnorodnoi zhidkost'yu
s neszhimaemoi odnorodnoi zhidkost'yu
![]() const
const![]() . Tak kak teplovaya energiya
. Tak kak teplovaya energiya ![]() ravna rabote, zatrachennoi
na szhatie dannogo gazovogo ob'ema, v sluchae neszhimaemoi zhidkosti
ravna rabote, zatrachennoi
na szhatie dannogo gazovogo ob'ema, v sluchae neszhimaemoi zhidkosti ![]() i,
sledovatel'no,
i,
sledovatel'no, ![]() . Eto vidno i iz formuly
. Eto vidno i iz formuly
![]() dlya
dlya ![]() . Polnaya energiya
. Polnaya energiya ![]() , ochevidno, ravna gravitacionnoi
, ochevidno, ravna gravitacionnoi ![]() .
.
4. ![]() . Sluchai
. Sluchai ![]() yavlyaetsya naibolee interesnym i fizicheski vazhnym. Kak my
uvidim nizhe, on osushestvlyaetsya i v belyh karlikah, i v bol'shih goryachih zvezdah,
gde
yavlyaetsya naibolee interesnym i fizicheski vazhnym. Kak my
uvidim nizhe, on osushestvlyaetsya i v belyh karlikah, i v bol'shih goryachih zvezdah,
gde
![]() (zdes'
(zdes'
![]() -- plotnost'
energii
-- plotnost'
energii
![]() erg
erg![]() sm
sm![]() ). I dazhe dlya Solnca naibolee blizki k real'nosti
politropnye modeli s
). I dazhe dlya Solnca naibolee blizki k real'nosti
politropnye modeli s ![]() .
.
V chem osobennost' etogo sluchaya? Vo-pervyh, teoriya politropnyh sharov pri dannom
uravnenii sostoyaniya (pri dannom ![]() ) i dannoi masse
) i dannoi masse ![]() ne pozvolyaet vychislit'
radius zvezdy. Krome togo, polnaya energiya zvezdy
ne pozvolyaet vychislit'
radius zvezdy. Krome togo, polnaya energiya zvezdy
![]() , t.e.
, t.e. ![]() .
.
Pochemu eto proishodit? Rassmotrim poryadkovye ocenki. Teplovaya energiya ![]() pri
pri ![]() po poryadku ravna
po poryadku ravna
![]() . Dlya gravitacionnoi energii
vsegda imeem
. Dlya gravitacionnoi energii
vsegda imeem
![]() . Polnaya energiya
. Polnaya energiya
![]() . Ochevidno, chto dlya raznyh
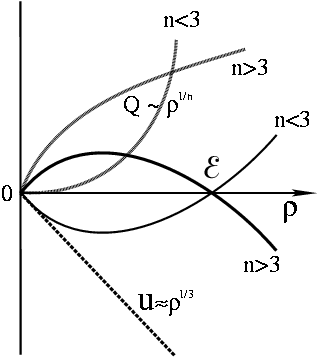
. Ochevidno, chto dlya raznyh ![]() energiya
energiya ![]() po raznomu zavisit ot
po raznomu zavisit ot
![]() (ris. 14).
V lyubom sluchae zavisimost'
(ris. 14).
V lyubom sluchae zavisimost'
![]() lineinaya.
Ochevidno, chto pri
lineinaya.
Ochevidno, chto pri
![]() sistema pri malyh vozmusheniyah nachnet razletat'sya
(
sistema pri malyh vozmusheniyah nachnet razletat'sya
(![]() stremitsya umen'shit'sya), a pri
stremitsya umen'shit'sya), a pri
![]() budet neogranichenno
szhimat'sya (kollapsirovat'). Ravnovesie vozmozhno tol'ko pri
budet neogranichenno
szhimat'sya (kollapsirovat'). Ravnovesie vozmozhno tol'ko pri
![]() , dlya etogo
sluchaya imeetsya tol'ko odno opredelennoe znachenie massy:
, dlya etogo
sluchaya imeetsya tol'ko odno opredelennoe znachenie massy:
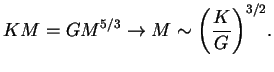
Takim obrazom, ravnovesnaya model' s ![]() imeet tri vazhnyh svoistva:
imeet tri vazhnyh svoistva:
1) ravnovesie vozmozhno tol'ko pri odnom opredelennom znachenii massy (esli ![]() fiksirovano), 2) polnaya energiya
fiksirovano), 2) polnaya energiya
![]() , 3) radius zvezdy
, 3) radius zvezdy ![]() mozhet byt'
lyubym, t.e. ravnovesie bezrazlichnoe.
mozhet byt'
lyubym, t.e. ravnovesie bezrazlichnoe.
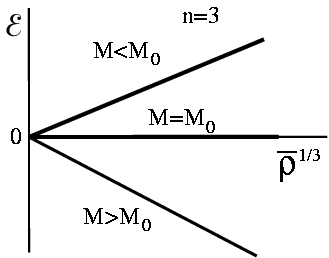
Rassmotrim kratko, kak vedet sebya polnaya energiya ![]() v zavisimosti ot
plotnosti pri
v zavisimosti ot
plotnosti pri
![]() (ris. 15). V sluchae
(ris. 15). V sluchae ![]() nabor krivyh dlya raznyh mass
imeet minimum, a pri
nabor krivyh dlya raznyh mass
imeet minimum, a pri ![]() maksimum. Ochevidno, chto tochki
maksimum. Ochevidno, chto tochki
![]() yavlyayutsya polozheniyami ravnovesiya, no pri
yavlyayutsya polozheniyami ravnovesiya, no pri ![]() eto ravnovesie
ustoichivo, a pri
eto ravnovesie
ustoichivo, a pri ![]() neustoichivo.
neustoichivo.
<< 2.2 Osnovnye parametry politropy | Oglavlenie | 2.4 Teoriya belyh karlikov >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |