Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Fizicheskie osnovy stroeniya i evolyucii zvezd
<< 2.3 Chastnye sluchai politropnyh ... | Oglavlenie | 2.5 Goryachie zvezdy >>

2.4 Teoriya belyh karlikov

Iz nablyudenii izvestno, chto massy belyh karlikov poryadka solnechnoi, no razmery sostavlyayut lish' sotuyu chast' solnechnogo radiusa (i dazhe men'she), t.e. belye karliki predstavlyayut soboi zvezdy s chrezvychaino bol'shoi plotnost'yu veshestva $ \rho \sim 10^5 \, - \, 10^9 \;$g$ /$sm$ ^3$. V takom sostoyanii obychnye atomy razrushayutsya, a veshestvo sostoit iz yader i svobodnyh elektronov, kotorye podchinyayutsya statistike Fermi-Diraka.

Poluchim uravnenie sostoyaniya dlya veshestva belyh karlikov.

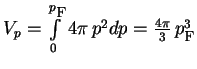V impul'snom prostranstve chislo kletok (sostoyanii) v 1 sm$ ^3$ ravno $ dn=d^3p/{(2\pi \hbar)}^3$, gde $ {(2\pi \hbar)}^3$ -- ob'em odnoi kletki (fazovoi yacheiki). Soglasno statistike Fermi-Diraka, v odnom sostoyanii mozhet nahodit'sya tol'ko odin elektron, i polnoe chislo elektronov $ N$, zaklyuchennoe v fazovom ob'eme $ V_p= \int\limits_0^{p_{\mbox{\sc f}}} 4\pi \,p^2dp={4\pi\over 3}\,p_{\mbox{\sc f}}^3$, s uchetom spina ravno

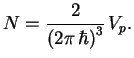
$\displaystyle N={2\over {(2\pi \,\hbar)}^3}\,V_p. $

Zdes' $ p_{\mbox{\sc f}}$ -- granichnyi impul's Fermi, vyshe kotorogo pri $ T=0$ vse urovni svobodny. Itak, chislo elektronov v odnom kubicheskom santimetre

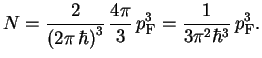
$\displaystyle N={2\over {(2\pi \,\hbar)}^3}\,{4\pi\over 3}\,p_{\mbox{\mbox{\sc f}}}^3={1\over {3\pi^2 \hbar^3}}\,p_{\mbox{\mbox{\sc f}}}^3. $

Udobno vyrazhat' $ p_{\mbox{\sc f}}$ v edinicah $ m_ec$, vvodya bezrazmernyi parametr $ x=p_{\mbox{\sc f}}/m_ec$. Togda $ N={(m_ec)^3\over {3\pi^2\,\hbar^3}}\,x^3$. Parametr $ x$ yavlyaetsya meroi relyativizma: pri $ x\ll 1$ elektrony nerelyativistskie, pri $ x\gg 1$ ul'trarelyativistskie. Kakoi plotnosti veshestva sootvetstvuet dannyi $ x$? Oboznachim cherez $ \mu_e$ molekulyarnyi ves na odin elektron, t.e. srednee chislo nuklonov na odin elektron ($ \mu_e=1$ dlya vodoroda, $ \mu_e=2$ dlya $ {}^{4}{\mathrm{He}}_2$ i $ \mu_e=2,2$ dlya $ {}^{56}{\mathrm{Fe}}_{26}$). Togda $ \rho=\mu_e \cdot1,6 \cdot 10^{-24}N=\mu_e \cdot 10^6 \,x^3\,[$g$ /$   sm$ ^3]$. Otsyuda sleduet, chto pri $ \rho<\mu_e \cdot 10^6\;$g$ /$sm$ ^3$ imeem $ x<1$, t.e. $ p_{\mbox{\sc f}}<m_ec$, i elektrony nerelyativistskie. Pri $ \rho>\mu_e \cdot 10^6\;$g$ /$sm$ ^3,\;p_{\mbox{\sc f}}>m_ec$.

Dlya vodoroda $ x=0,1$ osushestvlyaetsya pri plotnosti $ \rho=1000 \;$g$ /$sm$ ^3$ (dlya $ {}^{56}{\mathrm{Fe}}_{26}$ eto sootvetstvuet $ \rho=2200 \;$g$ /$sm$ ^3$). Fermi-energiya elektronov v etih usloviyah $ E_{\mbox{\sc f}}=p_{\mbox{\sc f}}^2 \;/{2m_e}=5 \cdot 10^{-3}m_e c^2=2500 \;\mbox{eV}$, chto v desyatki raz prevyshaet energiyu svyazi elektronov atoma vodoroda ( $ E_{\mbox{sv}}=13,6 \;\mbox{eV}$). Takim obrazom, pri $ x>0,1$ uzhe mozhno pol'zovat'sya teoriei vyrozhdennogo elektronnogo gaza.

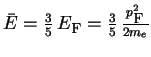Rassmotrim nerelyativistskuyu oblast' $ 0,1<x<1$. Srednyaya energiya elektronov v share s ob'emom $ {4\pi\over 3}\,p_{\mbox{\sc f}}^3$ ravna $ \bar E={3\over 5}\,E_{\mbox{\sc f}}={3\over 5}\, {p_{\mbox{\sc f}}^2 \over {2m_e}}$, t.e. $ \bar E \sim x^2$. Davlenie $ P\sim \rho E\sim x^5\sim \rho^{5/3}$, t.e. holodnoe nerelyativistskoe veshestvo predstavlyaet soboi gaz, podchinyayushiisya uravneniyu sostoyaniya s $ \gamma=5/3$:

$\displaystyle P=K\rho^{5/3}. $

Statistika Fermi (princip Pauli) opredelyaet konstantu. Dlya ideal'nogo (nekvantovogo) gaza $ K$ mozhet byt' lyubym. Esli ohlazhdat' goryachii gaz do temperatury $ T=0$, to $ K$ idet ne v nul', a stremitsya k opredelennomu predelu. Fermi-dvizhenie elektronov igraet rol' temperatury.

Z a d a ch a. Poluchite tochnuyu formulu dlya davleniya vyrozhdennogo nerelyativistskogo gaza $ P=10^{23}x^5\;$erg$ /$sm$ ^3$ i naidite vyrazhenie dlya $ K$ cherez fundamental'nye konstanty.

Vspominaya obshie formuly, vyvedennye dlya politropnyh konfiguracii, imeem ($ n=1,5$):

$\displaystyle M\sim x^{3/2},\;R\sim x^{-1/2}\sim M^{-1/3}. $

Privedem harakteristiki tipichnogo belogo karlika, sostoyashego iz geliya ($ \mu_e=2$) s massoi $ M=0,25\,M_\odot=0,5\cdot 10^{33}\;$g$ ;\;\rho_c=2,5\cdot 10^5\;$   g$ /$sm$ ^3,\;\rho=4\cdot 10^4\;$g$ /$sm$ ^3,\;R=1,4\cdot 10^9\;$   sm.

Strogo govorya, poluchennye vyshe rezul'taty otnosyatsya k absolyutno holodnomu veshestvu. Veshestvo belyh karlikov, kotorye my nablyudaem, imeyut otlichnuyu ot nulya temperaturu (oni svetyat!). No temperatura dazhe v neskol'ko millionov gradusov mala po sravneniyu s harakternoi fermi-energiei elektronov ( $ kT\ll E_{\mbox{\sc f}}$). Poetomu teplovoe dvizhenie plazmy ne sushestvenno pri raschete ravnovesiya i ustoichivosti belyh karlikov, hotya dlya rascheta ih ohlazhdeniya ono vazhno.

S uvelicheniem massy belogo karlika rastet $ x$, i pri nekotoroi velichine $ M\;x$ okazyvaetsya bol'she edinicy, elektronnyi gaz okazyvaetsya relyativistskim. Impul's elektrona svyazan so skorost'yu izvestnym sootnosheniem

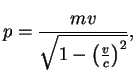
$\displaystyle p={mv\over \sqrt{1-{\left({v\over c}\right)}^2}}, $

a energiya elektrona

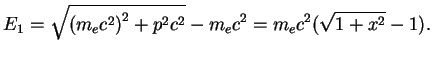
$\displaystyle E_1=\sqrt{{(m_ec^2)}^2+p^2c^2}-m_ec^2=m_ec^2(\sqrt{1+x^2}-1). $

Pri malyh $ x$, kogda $ \sqrt{1+x^2}\simeq 1+{x^2\over 2}$, poluchim uzhe izvestnuyu formulu

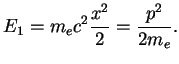
$\displaystyle E_1=m_ec^2{x^2\over 2}={p^2\over {2m_e}}. $

Pri $ x\gg 1$ (ostavlyaya tol'ko glavnyi chlen v razlozhenii) energiya odnogo elektrona $ E=m_ec^2x$, sledovatel'no, energiya edinicy massy $ E\sim x\sim \rho^{1/3}$, a davlenie $ P\sim \rho E\sim x^4\sim \rho^{4/3}$.

Takim obrazom, ul'trarelyativistskii vyrozhdennyi elektronnyi gaz podchinyaetsya uravneniyu sostoyaniya s pokazatelem $ \gamma=4/3$ (indeks politropy $ n=3$).

Nam uzhe izvestno (sm. vyshe), chto pri $ n=3$ ravnovesnoe sostoyanie vozmozhno tol'ko pri odnoi opredelennoi masse. Dlya vyrozhdennogo relyativistskogo veshestva (2.1) daet eto znachenie massy

$\displaystyle M_{\mbox{Ch}}={5,75\over \mu_e^2}\,M_\odot. $

Dlya $ \mu_e=2,\;M_{\mbox{Ch}}=1,44\,M_\odot$. Dlya vseh promezhutochnyh sluchaev imeyutsya tochnye chislennye raschety (ris. 16).

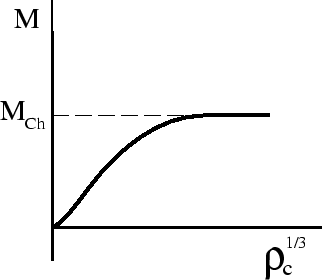
\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f16.ai}\hss} \end{wrapfigure}
Ris. 16.

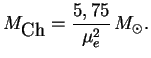
Itak, dlya holodnogo veshestva reshenie sushestvuet tol'ko pri $ M<M_{\mbox{Ch}}$ ( $ M_ {\mbox{Ch}}$ -- nazyvayut chandrasekarovskim predelom massy). Iz nablyudenii my znaem, chto est' goryachie zvezdy s massoi, bol'shei $ M_ {\mbox{Ch}}$. V rezul'tate evolyucii pri ostyvanii takih zvezd dolzhna proishodit' poterya ustoichivosti i kollaps (bystroe szhatie) zvezdy.

V n'yutonovskoi teorii bolee zhestkoe uravnenie sostoyaniya (naprimer, ottalkivanie yader) moglo by spasti zvezdu ot kollapsa. Odnako v OTO pri lyubom uravnenii sostoyaniya relyativistskie effekty vsegda privodyat k neustoichivosti i neogranichennomu kollapsu.

Poluchim, sleduya E.Solpiteru, vyrazhenie dlya predel'noi massy belogo karlika cherez fundamental'nye fizicheskie velichiny $ m_p,\;\hbar,\;c,\;G$, ili, drugimi slovami, naidem predel'noe chislo nuklonov $ N_{\mbox{Ch}}$, dlya kotoryh gravitaciya uravnoveshivaetsya davleniem vyrozhdennyh elektronov. Imeem $ M_{\mbox{Ch}}=m_pN_{\mbox{Ch}}$.

Iz konstant $ G,\;m_p,\;\hbar$ i $ c$ mozhno sostavit' tol'ko odno bezrazmernoe chislo: $ Gm_p^2/{\hbar c}\simeq 0,7\cdot 10^{-38}$ (analog postoyannoi tonkoi struktury $ e^2/{\hbar c}$). Po opredeleniyu $ N_{\mbox{Ch}}$ bezrazmerno i

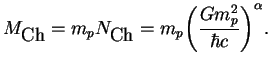
$\displaystyle M_{\mbox{Ch}}=m_pN_{\mbox{Ch}}=m_p{\left({Gm_p^2\over {\hbar c}}\right)}^\alpha. $

Kak naiti $ \alpha $? Vospol'zuemsya dlya etogo uravneniem sostoyaniya ul'trarelyativistskogo veshestva i naidem postoyannuyu $ K$ (priblizhenno)

$\displaystyle E_1=cp=c\hbar n^{1/3},\;P=nE_1=c\hbar n^{4/3},\;\rho=m_pn, $

t.e. $ P={c\hbar\over m_p^{4/3}}\,\rho^{4/3}$ i $ K={c\hbar\over m_p^{4/3}}$.

Dlya politropy $ n=3$ vyshe my poluchili $ M\sim {(K/G)}^{3/2}$. Podstavlyaya $ K$, imeem

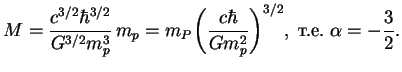
$\displaystyle M={c^{3/2}\hbar^{3/2}\over {G^{3/2}m_p^3}}\,m_p=m_P{\left({c\hbar\over {Gm_p^2}} \right)}^{3/2},\;\mbox{t.e.}\;\alpha=-{3\over 2}. $

Okonchatel'no

$\displaystyle M_{\mbox{Ch}}\sim m_p(10^{38})^{3/2},\;N_{\mbox{Ch}}\sim 10^{57}. $

Takoe bol'shoe chislo obuslovleno tem, chto konstanta gravitacionnogo vzaimodeistviya mala.


<< 2.3 Chastnye sluchai politropnyh ... | Oglavlenie | 2.5 Goryachie zvezdy >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 3.0 [golosov: 119]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya