
<< 2.4 Teoriya belyh karlikov
| Oglavlenie |
3. Perenos izlucheniya v zvezdah >>
Teper' rassmotrim drugoi predel'nyi sluchai, v kotorom glavnuyu rol' igraet davlenie
izlucheniya.
Napomnim uravnenie sostoyaniya dlya ideal'nogo gaza
zdes'
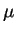
-- molekulyarnyi ves veshestva, t.e. velichina, kotoraya pokazyvaet, skol'ko
edinic atomnogo vesa prihoditsya na odnu chasticu (otlichaite
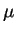
ot
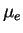
!).
Naprimer,
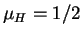
, no
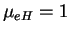
, i
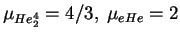
i t.p.
Pri vysokih temperaturah, kogda gaz polnost'yu ionizovan i yavlyaetsya odnoatomnym,
teplovaya energiya gramma veshestva ravna
S drugoi storony, pri vysokih temperaturah v termodinamike zvezdy vse bol'shuyu rol'
nachinaet igrat' davlenie izlucheniya. Dlya izlucheniya, nahodyashegosya v termodinamicheskom
ravnovesii (plankovskogo izlucheniya), plotnost' energii odnoznachno opredelyaetsya
temperaturoi (sm. nizhe, v
razdele 3.3)
Davlenie pri etom
V laboratornyh usloviyah izmenyayut ne plotnost'
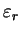
, a potok luchistoi
energii
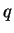
(Pochemu?), kotoryi svyazan s
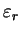
prostoi zavisimost'yu
(Poluchite koefficient 1/4 v etoi formule.) Takim obrazom,
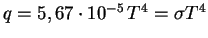
(zakon Stefana-Bol'cmana). Po formule Einshteina plotnost' massy
izlucheniya
Imeetsya shirokaya oblast' astrofizicheskih uslovii, kogda davlenie i energiya izlucheniya
i veshestva sravnimy, no plotnost' massy izlucheniya mnogo men'she plotnosti massy
veshestva (
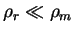
). Vypishem teper' vyrazheniya dlya polnogo davleniya veshestva
i izlucheniya
Rassmotrim model' zvezdy, v kotoroi svyaz' mezhdu plotnost'yu i temperaturoi daetsya
formuloi
gde
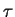
-- postoyannyi mnozhitel'. Togda davlenie veshestva
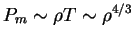
i davlenie izlucheniya
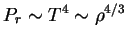
, t.e. v takoi modeli
otnoshenie davleniya izlucheniya i veshestva postoyanno po zvezde i
Otmetim, chto v etom sluchae entropiya
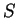
menyaetsya (Kak? Rastet ili padaet naruzhu?).
Vvedem velichinu
togda
Parametr
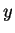
imeet prostoi smysl:
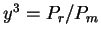
.
Takim obrazom,
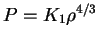 , i my imeem uzhe znakomoe nam uravnenie politropy
, i my imeem uzhe znakomoe nam uravnenie politropy
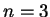 . My znaem, chto v etom sluchae ravnovesie vozmozhno tol'ko pri odnom znachenii
massy. Podstavlyaya
. My znaem, chto v etom sluchae ravnovesie vozmozhno tol'ko pri odnom znachenii
massy. Podstavlyaya 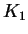 v formulu (2.1), poluchim
v formulu (2.1), poluchim
Ispol'zuya etu formulu, mozhno ocenit' rol' davleniya izlucheniya dlya zvezdy dannoi massy
(sm. tabl. 2, v kotoroi prinyato
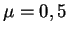
).
Tablica 2.2:
Rost davleniya v zavisimosti ot massy zvezdy (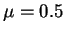 )
)
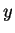 |
0.05 |
0.1 |
0.7 |
1 |
2 |
10 |
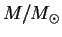 |
0.85 |
2.4 |
70 |
215 |
5800 |
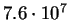 |
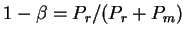 |
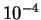 |
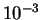 |
0.25 |
0.5 |
0.89 |
0.999 |
Iz tablicy 2 vidno, chto zvezda s massoi
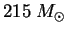 yavlyaetsya granichnoi (
yavlyaetsya granichnoi (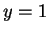 ).
Kak pokazal A.Eddington, dlya zvezd s massoi poryadka
).
Kak pokazal A.Eddington, dlya zvezd s massoi poryadka
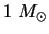 rol' davleniya
izlucheniya prenebrezhima, a dlya zvezd s
rol' davleniya
izlucheniya prenebrezhima, a dlya zvezd s
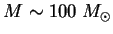 davlenie izlucheniya
yavlyaetsya dominiruyushim.
davlenie izlucheniya
yavlyaetsya dominiruyushim.
Primenim teoremu viriala k postroennoi vyshe modeli. S uchetom izlucheniya teplovaya
energiya zvezdy
Po teoreme viriala gravitacionnaya energiya zvezdy
Polnaya energiya zvezdy
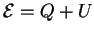
t.e. zvezda gravitacionno svyazana, no eta svyaz' ravna tol'ko toi dole energii,
kotoraya opredelyaetsya veshestvom
poetomu pri
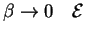
-- malo. V etoi modeli my iskusstvenno vveli
politropu
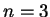
, no entropiya ne postoyanna po zvezde (esli
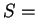
const po zvezde,
to pri
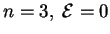
). Podcherknem raznicu mezhdu pokazatelem adiabaty
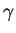
i pokazatelem politropy
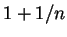
. Voz'mem odnoatomnyi nerelyativistskii gaz (
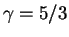
), dlya kotorogo
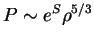
. Pust' raspredelenie entropii po zvezde
opredelyaetsya zavisimost'yu
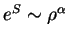
, togda davlenie i plotnost' svyazany
sootnosheniem
Struktura zvezdy budet opredelyatsya pokazatelem politropy (zdes'
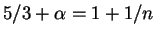
),
a ustoichivost' zavisit ot pokazatelya adiabaty, t.e. ot uprugosti veshestva (v nashei
modeli
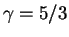
).
Za schet raspredeleniya entropii my mozhem poluchit' ustoichivuyu zvezdu, naprimer, s
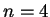 . V rassmatrivaemoi vyshe modeli
. V rassmatrivaemoi vyshe modeli 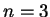 , no polnaya energiya etoi zvezdy ne
ravnyalas' nulyu, tak kak model' neizentropichna. Ustoichivost' zvezdy opredelyaetsya
ne raspredeleniem veshestva, a tem, kak ono vedet sebya pri szhatii (t.e. ego uprugost'yu!).
, no polnaya energiya etoi zvezdy ne
ravnyalas' nulyu, tak kak model' neizentropichna. Ustoichivost' zvezdy opredelyaetsya
ne raspredeleniem veshestva, a tem, kak ono vedet sebya pri szhatii (t.e. ego uprugost'yu!).
<< 2.4 Teoriya belyh karlikov
| Oglavlenie |
3. Perenos izlucheniya v zvezdah >>
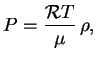
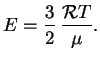
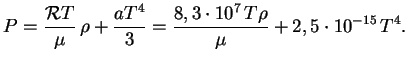
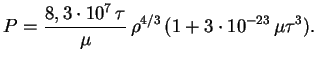
![]() , i my imeem uzhe znakomoe nam uravnenie politropy
, i my imeem uzhe znakomoe nam uravnenie politropy
![]() . My znaem, chto v etom sluchae ravnovesie vozmozhno tol'ko pri odnom znachenii
massy. Podstavlyaya
. My znaem, chto v etom sluchae ravnovesie vozmozhno tol'ko pri odnom znachenii
massy. Podstavlyaya ![]() v formulu (2.1), poluchim
v formulu (2.1), poluchim
![]() yavlyaetsya granichnoi (
yavlyaetsya granichnoi (![]() ).
Kak pokazal A.Eddington, dlya zvezd s massoi poryadka
).
Kak pokazal A.Eddington, dlya zvezd s massoi poryadka
![]() rol' davleniya
izlucheniya prenebrezhima, a dlya zvezd s
rol' davleniya
izlucheniya prenebrezhima, a dlya zvezd s
![]() davlenie izlucheniya
yavlyaetsya dominiruyushim.
davlenie izlucheniya
yavlyaetsya dominiruyushim.
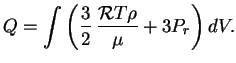
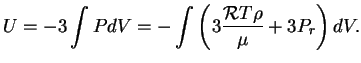
![]()
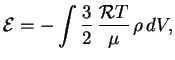
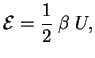
![]() . V rassmatrivaemoi vyshe modeli
. V rassmatrivaemoi vyshe modeli ![]() , no polnaya energiya etoi zvezdy ne
ravnyalas' nulyu, tak kak model' neizentropichna. Ustoichivost' zvezdy opredelyaetsya
ne raspredeleniem veshestva, a tem, kak ono vedet sebya pri szhatii (t.e. ego uprugost'yu!).
, no polnaya energiya etoi zvezdy ne
ravnyalas' nulyu, tak kak model' neizentropichna. Ustoichivost' zvezdy opredelyaetsya
ne raspredeleniem veshestva, a tem, kak ono vedet sebya pri szhatii (t.e. ego uprugost'yu!).