Astronet > 3.2 Osnovnye ponyatiya teorii ravnovesnogo izlucheniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 3.1 Vvedenie | Oglavlenie | 3.3 Kinetika fotonov ... >>

3.2 Osnovnye ponyatiya teorii ravnovesnogo izlucheniya

Pust' -- chislo fotonov v kletke fazovogo prostranstva, t.e. chislo zapolneniya, kotoroe bezrazmerno. Dlya ``yashika'' dannogo ob'ema mozhno govorit' o chisle sostoyanii. Esli sostoyanii mnogo, to chislo urovnei v ob'eme i v impul'snom ob'eme est'

$\displaystyle V\,d^3p/{(2\pi\hbar)}^3.$

Togda plotnost' chisla fotonov

$\displaystyle N={2\over {(2\pi\hbar)}^3}\,\int\limits_0^\infty nd^3p\,[$ sm $\displaystyle ^{-3}],$

(3.1)

gde koefficient 2 uchityvaet dva vozmozhnyh sostoyaniya s raznymi polyarizaciyami.

Izvestno, chto impul's fotona $\vec p$ svyazan s volnovym vektorom $\vec k$ formuloi De Broilya

$\displaystyle \vec p=\hbar\vec k.$

Podstavlyaya eto vyrazhenie v formulu (3.1), poluchim bolee naglyadnoe vyrazhenie dlya plotnosti chisla fotonov

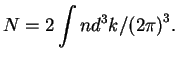
$\displaystyle N=2\int nd^3k/{(2\pi)}^3.$

Poskol'ku $\vert k\vert=2\pi/\lambda$ , ochevidna razmernost' $N\sim 1/\lambda^3\sim$ $\mbox {sm}^{-3}$ i, krome togo, ischezaet postoyannaya Planka $\hbar$ , kotoraya byla vazhna tol'ko pri podschete chisla sostoyanii.

V sfericheskoi sisteme koordinat

$\displaystyle d^3p=p^2dpd\,\Omega\;\;\;(p=\vert\vec p\vert).$

V sluchae sfericheskoi simmetrii $\int d\Omega=4\pi$ i

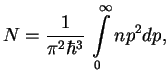
$\displaystyle N={1\over {\pi^2 \hbar^3}}\,\int\limits_0^\infty np^2dp,$

gde

-- funkciya tol'ko ot $p:\;n=n(p)$ .

Poskol'ku energiya odnogo fotona

$\displaystyle E_{ph}=\hbar\,\omega=h\,\nu=cp,$

to plotnost' energii izlucheniya (fotonnogo gaza)

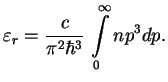
$\displaystyle \varepsilon_r={c\over {\pi^2\hbar^3}}\,\int\limits_0^\infty np^3dp.$

Krome plotnosti energii $\varepsilon_r$ vazhnoi harakteristikoi yavlyaetsya spektral'naya intensivnost' izlucheniya $F_\nu\;([F_\nu]=$ ergsm s Gc ster -- velichina, kotoraya pri otsutstvii poglosheniya ili rasseivaniya ne zavisit ot rasstoyaniya do istochnika. Iz nablyudenii vsegda poluchaetsya $F_\nu$ , a v fiziku dela vhodit chislo zapolneniya .

Poluchim svyaz' mezhdu $F_\nu$ i :

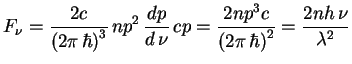
$\displaystyle F_\nu={2c\over {(2\pi\,\hbar)}^3}\,np^2\,{dp\over d\,\nu}\,cp={2np^3c\over {(2 \pi\,\hbar)}^2}={2nh\,\nu\over \lambda^2}$

(pri etom my ispol'zovali, chto $dp/d\,\nu=2\pi\hbar/c$ ). $F_\nu$ imeet smysl energii, prohodyashei cherez ploshadku $\lambda^2$ v edinicu vremeni v edinichnom intervale chastot, poetomu $[F_\nu]=$ erg

sm $^2\,$ c $\,$ Gc.

V obshem sluchae (i pri otsutstvii ravnovesiya) svyaz' mezhdu $\varepsilon_r$ i $F_\nu$ daetsya formuloi

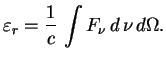
$\displaystyle \varepsilon_r={1\over c}\,\int F_\nu\,d\,\nu\,d\Omega.$

<< 3.1 Vvedenie | Oglavlenie | 3.3 Kinetika fotonov ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

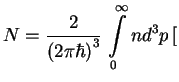Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce