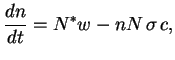Astronet > 3.3 Kinetika fotonov i formula Planka

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 3.2 Osnovnye ponyatiya ... | Oglavlenie | 3.4 Tormoznoe izluchenie zaryadov >>

3.3 Kinetika fotonov i formula Planka

Rassmotrim teper', kak menyaetsya funkciya raspredeleniya fotonov s uchetom ih vzaimodeistviya s veshestvom. Pust' imeetsya sreda iz atomov, kotorye mogut nahodit'sya tol'ko v dvuh sostoyaniyah -- v osnovnom i vozbuzhdennom, i raznost' mezhdu etimi urovnyami ravna $h\nu$ , i pust' imeetsya atomov/ sm v osnovnom sostoyanii i -- v vozbuzhdennom. Togda kineticheskoe uravnenie dlya chisla zapolneniya mozhno zapisat' v vide

$\displaystyle {dn\over {dt}}=N^*w-nN\,\sigma\,c,$

(3.2)

gde pervyi chlen v pravoi chasti uchityvaet uvelichenie chisla kvantov v rezul'tate ih ispuskaniya vozbuzhdennymi atomami s veroyatnost'yu

, a vtoroi chlen -- umen'shenie

pri pogloshenii ih nevozbuzhdennymi atomami, $\sigma\;[$ sm

-- sechenie vozbuzhdeniya. Iz kvantovoi mehaniki izvestno, chto veroyatnost' poglosheniya $N \sigma c$ tozhdestvenno ravna veroyatnosti ispuskaniya

(tak kak pryamoi i obratnyi processy opisyvayutsya odnim matrichnym elementom). V kineticheskom uravnenii (3.2) ispuskanie kvantov opredelyaetsya tol'ko svoistvami veshestva i ego sostoyaniem. Odnako sushestvuet vynuzhdennoe, ili inducirovannoe, ispuskanie: veroyatnost' ispuskaniya kvantov v kakoe-to sostoyanie proporcional'no chislu kvantov, uzhe imeyushihsya v etom sostoyanii. Kak govorit teoriya (i opyt), polnaya veroyatnost' ispuskaniya est'

, i s uchetom vynuzhdennogo izlucheniya kineticheskoe uravnenie zapishetsya v vide

$\displaystyle {dn\over {dt}}=w[N^*(1+n)-Nn]=w[N^*-n(N-N^*)].$

Otmetim, chto pri

vozmozhen eksponencial'nyi rost plotnosti izlucheniya (mazernyi effekt). A v astrofizicheskih usloviyah takaya neravnovesnaya situaciya mozhet vstrechat'sya tol'ko v gazovyh tumannostyah (istochniki ON i t.p.).

V usloviyah lokal'nogo termodinamicheskogo ravnovesiya, kotoroe osushestvlyaetsya vnutri zvezd, nichego podobnogo byt' ne mozhet, tak kak raspredelenie atomov po energiyam opisyvaetsya formuloi Bol'cmana:

$\displaystyle N^*=Ne^{-E/kT}.$

Poskol'ku $E=h\nu$

$\displaystyle {dn\over {dt}}=w N[e^{-h\nu/kT}-n(1-e^{-h\nu/kT})].$

V ravnovesii

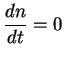$\displaystyle {dn\over {dt}}=0\;$ i $\displaystyle$

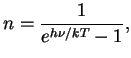
$\displaystyle n={1\over {e^{h\nu/kT}-1}},$

eto formula Planka.

Legko ubedit'sya, chto ravnovesie ustoichivo. Zapishem uravnenie kinetiki v vide

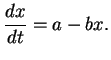
$\displaystyle {dx\over {dt}}=a-bx.$

Vvedem

, togda ${dy\over {dt}}=-by$ , i obshee reshenie est'

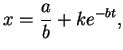
$\displaystyle x={a\over b}+ke^{-bt},$

-- eto ravnovesnoe reshenie, a obshee reshenie opisyvaet priblizhenie k nemu, chto i dokazyvaet ustoichivost'.

Rassmotrim predel'nye sluchai formuly Planka.

1. Relei -- Dzhinsovskaya oblast'. $x=h\nu/kT\ll 1$ . Ispol'zuya razlozhenie $e ^x=1+x+\ldots$ , poluchim dlya chisla zapolneniya: $n={1\over x}={kT\over {h\nu}}\gg 1$ , a dlya intensivnosti $F_\nu={2nh\,\nu\over \lambda^2}={2kT\over \lambda^2}$ . Kak vidim, v poslednee vyrazhenie postoyannaya Planka ne vhodit. Formula $F_\nu={2kT\over \lambda^2}$ pervonachal'no byla poluchena v klassicheskoi teorii. Kolebaniya elektromagnitnogo polya mozhno predstavit' naborom oscillyatorov, kazhdyi iz kotoryh imeet energiyu . Yasno, chto formula Releya -- Dzhinsa neprimenima pri malyh $\lambda$ iz-za rashodimosti integrala $\int F_\nu d\nu$ (ul'trafioletovaya katastrofa). Krome togo, pri $h\nu /kT>1$ ona ne soglasuetsya s opytom. No pri $h\nu /kT>1$ sleduet ispol'zovat' drugoe predel'noe razlozhenie formuly Planka.

2. Vinovskaya oblast': $h\nu/kT>1,\;n=e^{-h\nu/kT}\ll 1$ . Eto raspredelenie imeet vid formuly Bol'cmana. Ee my poluchili by, esli by prenebregli v kineticheskom uravnenii inducirovannym izlucheniem (tak kak $n\ll 1$ ). Tochnoe vyrazhenie dlya plotnosti energii

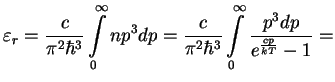
$\displaystyle \varepsilon_r={c\over {\pi^2\hbar^3}}\int\limits_0^\infty np^3dp={c\over {\pi^2\hbar^3}} \int\limits_0^\infty {p^3dp\over {e^{cp\over {kT}}-1}}=$

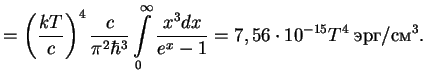
$\displaystyle ={\left({kT\over c}\right)}^4\,{c\over {\pi^2\hbar^3}}\int\limits_0^\infty {x^3dx\over {e^x-1}}=7,56\cdot 10^{-15}T^4\;\mbox{erg}/\mbox{sm}^3.$

Zdes' ispol'zovan tablichnyi integral:

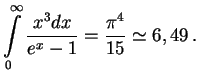
$\displaystyle \int\limits_0^\infty {x^3dx\over {e^x-1}}={\pi^4\over {15}}\simeq 6,49\,.$

Maksimum funkcii raspredeleniya energii po chastote prihoditsya na $x\simeq 2,7$ , t.e. $h\nu=2,7\;kT$ .

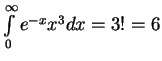Zamechanie. Otmetim, chto formula Vina ochen' udobna dlya priblizhennogo vychisleniya integral'nyh velichin v teorii izlucheniya. Naprimer, pri vychislenii polnoi energii tochnoe vyrazhenie $\int {x^3dx\over {e^x-1}}$ mozhno zamenit' priblizhennym integralom $\int e^{-x}x^3dx$ . V etom sluchae $x_{\max}=3$ , a integral $\int\limits_0^ \infty e^{-x}x^3dx=3!=6$ (sravnite s tochnym znacheniem $\pi^4/15=6,49$ ). Vinovskoe priblizhenie yavlyaetsya pervym chlenom v razlozhenii funkcii Planka:

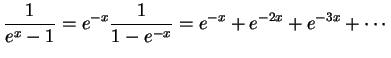
$\displaystyle {1\over {e^x-1}}=e^{-x}{1\over {1-e^{-x}}}=e^{-x}+e^{-2x}+e^{-3x}+\cdots$

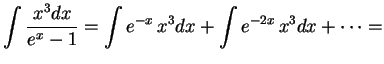
$\displaystyle \int {x^3dx\over {e^x-1}}=\int e^{-x}\,x^3dx+\int e^{-2x}\,x^3dx+\cdots=$

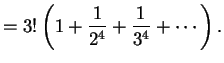
$\displaystyle =3!\left(1+{1\over 2^4}+{1\over 3^4}+\cdots\right).$

Eto vyrazhenie naglyadno demonstriruet rol' ostal'nyh chlenov, kotorye dayut vklad okolo 7%.

Ispol'zuya Vinovskoe priblizhenie, legko vychislit', kakaya dolya energii izluchaetsya v oblasti chastot b $\acute {\mbox{o}}$ l'shih nekotoryh. Naprimer,

$x>3,\;\;\;h\nu>3\,kT$ -- 60%

$x>4,\;\;\;h\nu>4\,kT$ -- 40%

$x>10,\;\;\;h\nu>10\,kT$ -- 6%.

Otmetim, chto nesmotrya na eksponencial'nyi mnozhitel' sushestvennaya dolya energii (6%) izluchaetsya pri .

Ranee v kineticheskom uravnenii ${dn\over {dt}}=N^*w(1+n)-N\,\sigma cn,\; w=\sigma c$ , my predpolagali, chto -- veroyatnost' perehoda s odnogo urovnya na drugoi. V deistvitel'nosti urovni imeyut nekotoruyu shirinu (razmyty), i polnaya veroyatnost' perehoda opredelyaetsya integralom (Razmernost' s $^ {-1}$ v otlichie ot sm $^3\cdot$ s $^ {-1}$ .)

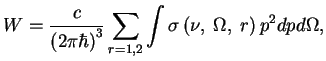
$\displaystyle W={c\over {(2\pi\hbar)}^3}\sum\limits_{r=1,2} \int \sigma\,(\nu,\;\Omega,\;r)\,p^2dpd\Omega,$

gde $\sum\limits_{r=1,2}$ uchityvaet dva vozmozhnyh sostoyaniya polyarizacii. Raschet secheniya $\sigma$ (klassicheskii, libo kvantovomehanicheskii) daet formulu

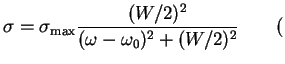$\displaystyle \sigma=\sigma_{\max}{(W/2)^2\over {(\omega-\omega_0)^2+(W/2)^2}}\qquad($ formula Lorenca $\displaystyle ).$

Podstavlyaya eto vyrazhenie v integral dlya

, kotoryi zapishem v vide

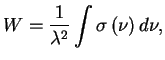
$\displaystyle W={1\over \lambda^2}\int \sigma\,(\nu)\,d\nu,$

poluchim, chto $\sigma_{\max}=\lambda^2/\pi$ .

Rassmotrim prichiny razmytosti urovnei. V nulevom priblizhenii po kvantovoi teorii vozmozhny tol'ko strogo opredelennye energeticheskie urovni. V sleduyushem priblizhenii poyavlyaetsya vozmozhnost' perehodov mezhdu energeticheskimi sostoyaniyami atoma, i v silu nestacionarnosti sostoyanii urovni energii okazyvayutsya razmytymi -- po principu neopredelennosti na velichinu $\Delta E\sim hW$ . Ispuskaemye kvanty budut imet' razmytost' poryadka po chastote.

Veroyatnosti raspada mogut byt' raznymi. Naprimer: perehod s urovnya v osnovnoe sostoyanie atoma vodoroda proishodit za $1,6\cdot 10^{-9}\;$ s, v to vremya kak v linii v 21 sm za let. Vazhno, chto pri etom izmenyaetsya tol'ko shirina $\sigma$ , proporcional'naya , no vsegda $\sigma_{\max}=\lambda^2/\pi$ (ris. 17).

$\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f17.ai}\hss} \end{wrapfigure}$

Ris. 17.

Vse eto verno dlya odnogo izolirovannogo atoma. V deistvitel'nosti atomy vzaimodeistvuyut. V real'nom gaze sushestvuet ryad prichin, po kotorym spektral'nye linii rasshiryayutsya: stolknoveniya chastic, doppler-effekt, shtark-effekt. Pri etom mozhet sluchit'sya, chto $\sigma_{\max}$ okazhetsya men'she. Naprimer, iz-za doppler-effekta dolzhen sohranyat'sya integral $\int \sigma d\omega$ i $\sigma_{\max}$ snizhaetsya.

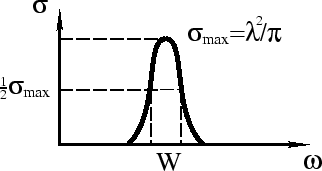
Sleduet pomnit', chto estestvennaya vysota secheniya $\sigma_{\max}=\lambda^2/\pi$ sohranyaetsya, esli net razmyvayushih ego mehanizmov. V kachestve primera mozhno rassmotret' effekt Messbauera. Esli prinyat' sootvetstvuyushie mery (grubo govorya, zakrepit' atomy v kristallicheskoi reshetke), to mozhno nablyudat' rezonansnye linii $\gamma$ -izlucheniya yader, pri etom sechenie kak raz ravno $\lambda^2/\pi$ .

<< 3.2 Osnovnye ponyatiya ... | Oglavlenie | 3.4 Tormoznoe izluchenie zaryadov >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce