Astronet > 3.4 Tormoznoe izluchenie zaryadov

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 3.3 Kinetika fotonov i | Oglavlenie | 3.5 Rasseyanie izlucheniya na ... >>

3.4 Tormoznoe izluchenie zaryadov

Zaryad (elektron), dvizhushiisya ravnomerno i pryamolineino, ochevidno, nichego ne izluchaet (chtoby v etom ubedit'sya, dostatochno pereiti v sistemu otscheta, gde on pokoitsya). Iz klassicheskoi elektrodinamiki izvestno, chto kolichestvo energii, izluchaemoi zaryadom v edinicu vremeni, opredelyaetsya ego uskoreniem:

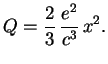
$\displaystyle Q={2\over 3}\,{e^2\over c^3}\,x^2.$

Podcherknem, chto eta formula otnositsya k odnomu zaryadu. Esli uskoryayutsya dva zhestko svyazannyh elektrona, to

vozrastaet v 4 raza (tak kak $Q\sim e^2$ ). Takim obrazom, nel'zya prosto summirovat'

ot razlichnyh zaryadov.

Nizhe my budem rassmatrivat' izluchenie elektrona pri uskorenii ego vo vneshnem elektricheskom pole, skazhem, v kulonovskom pole iona. Vdali elektron dvizhetsya prakticheski s postoyannoi skorost'yu. Uskorenie elektrona maksimal'no pri prolete na minimal'nom rasstoyanii ot iona. Ochevidno, pri etom maksimal'no i izluchenie. Nas budet interesovat' i spektral'nyi sostav izlucheniya $Q_\nu\simeq e^2x_\nu^2/c ^3$ , gde $x_\nu$ -- fur'e-komponenta uskoreniya.

Zaimemsya izlucheniem dlinnyh voln. Fur'e-komponenta uskoreniya

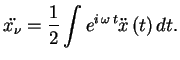
$\displaystyle \ddot {x_\nu}={1\over 2}\int e^{i\,\omega\,t}\ddot x\,(t)\,dt.$

Esli $\vert\omega t\vert<1$ (dlinnye volny)

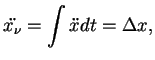
$\displaystyle \ddot {x_\nu}=\int \ddot xdt=\Delta x,$

t.e. $\ddot {x_\nu}$ ravno izmeneniyu skorosti za vremya poleta i ne zavisit ot $\nu$ . Togda pri odnom stolknovenii v edinichnom intervale chastot izluchaetsya energiya

$\displaystyle Q_\nu\,\left[{\mbox{erg}\over \mbox{Gc}}\right]={4\over 3}\,e^2\,{(\Delta x)^2\over c^3}.$

(3.3)

Podcherknem eshe raz, chto eto vyrazhenie spravedlivo tol'ko pri $\omega<1/\tau$ , gde $\tau$ -- dlitel'nost' sobytiya (stolknoveniya) (rassmatrivaem dlinnye volny). Zametim, chto razmernost' $Q_\nu$ v formule (3.3) izmenilas' na s

po sravneniyu s razmernost'yu $Q\,\left[{\mbox{erg}\over \mbox{s}}\right]$ , tak kak my pereshli snachala na edinichnyi interval chastot i, krome togo, rassmatrivaem energiyu, izluchennuyu ne v sekundu, a za vse vremya proleta.

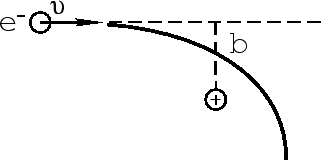
$\begin{wrapfigure}{l}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f18.ai}\hss} \end{wrapfigure}$

Ris. 18.

Legko podschitat' izmenenie impul'sa elektrona, proletayushego v pole iona, pervonachal'no imeyushego skorost' i pricel'nyi parametr (ris. 18):

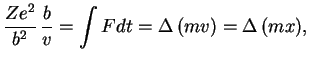
$\displaystyle {Ze^2\over b^2}\,{b\over v}=\int Fdt=\Delta\,(mv)=\Delta\,(mx),$

otkuda

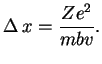
$\displaystyle \Delta\,x={Ze^2\over {mbv}}.$

Pust' na ion s beskonechnosti padaet puchok elektronov so skorost'yu i plotnost'yu . Cherez kol'co ploshad'yu $2\pi bdb$ okolo polya iona prohodit $N_ev2\pi bdb$ elektronov v sekundu. Kazhdyi iz nih v edinichnom intervale chastot izluchaet $Q_\nu$ . Esli v 1 sm nahoditsya ionov, to polnyi potok energii, izluchaemyi v edinicu vremeni, ochevidno, raven integralu (logarifmicheskii mnozhitel' opuskaem)

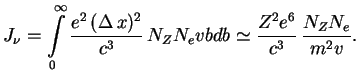
$\displaystyle J_\nu=\int\limits_0^\infty {e^2\,(\Delta\,x)^2\over c^3}\,N_ZN_evbdb\simeq {Z^2e^6\over c^3}\,{N_ZN_e\over {m^2v}}.$

Iz kvantovoi mehaniki izvestno, chto kvant chastotoi $\nu$ mozhet izluchit' tol'ko elektron, imeyushii energiyu bol'she $mv_{min}^2/2=h\nu$ . Poetomu v polnoe vyrazhenie voidet mnozhitel' $e^{-h\nu/kT}$

$\displaystyle J_\nu={32\pi\over 3}\,{\left({2\pi\,m\over {3kT}}\right)}^{1/2}\,... ...^{-{h\nu\over {kT}}}\;\left[{\mbox{erg}\over {\mbox{sm}^3 \mbox{s Gc}}}\right]$

(formula tormoznogo ili

-izlucheniya). V etoi formule uchteno, chto elektrony imeyut maksvellovskoe raspredelenie po skorostyam s temperaturoi

. Kak vidim, chislo kvantov s $h\nu>kT$ eksponencial'no malo. Eto svyazano s tem, chto bol'shie kvanty izluchayutsya elektronami s bol'shimi energiyami, sosredotochennymi v ``hvoste'' maksvellovskogo raspredeleniya.

Pri dannom ob'emnom koefficiente $J_\nu$ izmenenie intensivnosti $F_\nu$ v prozrachnoi srede, ochevidno, opredelyaetsya uravneniem

$\displaystyle (n\nabla\,F_\nu)={dF_\nu\over {dx}}={J_\nu\over {4\pi}},$

gde

-- koordinata vdol' proizvol'nogo napravleniya

. Prozrachnyi istochnik ( maly pogloshenie i inducirovannoe izluchenie) daet odnu i tu zhe osveshennost' v lyuboi tochke sfery s radiusom mnogo bol'she razmerov istochnika nezavisimo ot formy istochnika. V obshem sluchae s uchetom inducirovannogo izlucheniya i poglosheniya izmenenie intensivnosti vdol' opredelennogo napravleniya vyrazhaetsya uravneniem

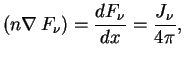
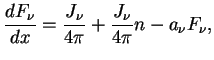
$\displaystyle {dF_\nu\over {dx}}={J_\nu\over {4\pi}}+{J_\nu\over {4\pi}}n-a_\nu F_\nu,$

gde $a_\nu\;[$ sm $^{-1}]$ -- koefficient poglosheniya.

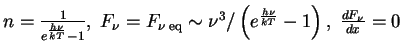Pri polnom termodinamicheskom ravnovesii $n={1\over {e^{h\nu\over {kT}}-1}},\;F_ \nu=F_{\nu\;\rm eq}\sim \nu^3/\left({e^{h\nu\over {kT}}-1}\right),\;{dF_\nu\over {dx}}=0$ . Poluchaem, chto otnoshenie ob'emnogo koefficienta izlucheniya veshestva $J_\nu$ k ego koefficientu poglosheniya $a_\nu$ est' universal'naya funkciya $\nu$ i (zakon Kirhgofa):

$\displaystyle J_\nu/a_\nu=8\pi\,h\,\nu^3\,e^{-{h\nu\over {kT}}}/c^2.$

Takim obrazom, esli vychisleno $J_\nu$ , to $a_\nu$ nahoditsya elementarno, i dlya svobodno-svobodnyh

-perehodov poluchaem

$\displaystyle a_\nu={4\over 3}\,{\left({2\pi\over {3kTm}}\right)}^{1\over 2}\,{... ...{hcm\,\nu^3}}={3,7\cdot 10^8Z^2N_ZN_e\over {\nu^3\sqrt{T}}}\;[\mbox{sm}^{-1}].$

Ob'edinim v pravoi chasti uravneniya perenosa chleny, otvechayushie inducirovannomu izlucheniyu i poglosheniyu, tak kak oba oni proporcional'ny neizvestnoi funkcii koordinat -- intensivnosti izlucheniya $F_\nu$ (poskol'ku $n\sim F_\nu$ ). V chlene inducirovannogo ispuskaniya $J_\nu n/4\pi$ vyrazim $J_\nu$ cherez koefficient poglosheniya $a_\nu$ , togda pravaya chast' primet vid ${J_\nu\over 4\pi}-a_\nu(1-e^{-{h\nu\over kT}})\,F_\nu$ .

Otsyuda vidno, chto vynuzhdennoe ispuskanie mozhno traktovat' kak nekoe umen'shenie poglosheniya: chast' kvantov kak by pogloshaetsya i tut zhe ispuskaetsya s toi zhe chastotoi i v tom zhe napravlenii s veroyatnost'yu $e^{-h\nu/kT}$ . Fizicheski takie akty nikak sebya ne proyavlyayut i ih mozhno voobshe isklyuchit' iz rassmotreniya, vvodya

$\displaystyle a'_\nu=a_\nu\,(1-e^{-{h\nu\over kT}}).$

Uravnenie perenosa prinimaet vid

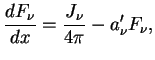
$\displaystyle {dF_\nu\over dx}={J_\nu\over 4\pi}-a'_\nu F_\nu,$

i vzaimodeistvie izlucheniya s veshestvom mozhno predstavit' tak, kak budto sushestvuet tol'ko spontannoe ispuskanie i effektivnoe pogloshenie, opisyvaemoe koefficientom $a'_\nu$ .

Koefficient istinnogo poglosheniya $a_\nu\sim \nu^{-3}$ , no pri $h\nu<kT$ effektivnoe pogloshenie $a'_\nu\sim \nu^{-2}$ i v ravnovesii eto daet relei-dzhinsovskuyu formulu dlya intensivnosti $F_{\rm eq}\sim {J_\nu\over a'_\nu}\sim\nu^2$ (koefficient izlucheniya $I_\nu$ pri $h\nu<kT$ fakticheski postoyanen). Ispol'zuya zakon Kirhgofa ${J_\nu\over 4\pi}=a'_\nu F_{\nu\;\rm eq}$ , zapishem v obshem sluchae uravnenie perenosa v vide

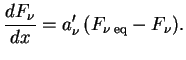
$\displaystyle {dF_\nu\over dx}=a'_\nu\,(F_{\nu\;\rm eq}-F_\nu).$

Eto uravnenie zapisano dlya koordinaty, izmenyayusheisya vdol' lucha zreniya. Iz nego vidno, chto, esli pri $x=0\;F_\nu=0$ , to snachala, pri malyh $x<1/a'_\nu,\;F_\nu$ stremitsya k $F_{\nu\;\rm eq}$ lineino: $F_\nu=a'_\nu F_{\nu\;\rm eq}x$ , a zatem pri $x>1 /a'_\nu$ bystro ustanavlivaetsya ravnovesie, pri kotorom $F_\nu=F_{\nu\;\rm eq}$ . Esli razmery izluchayushego oblaka (sloya)

men'she $1/a'_\nu$ , to ono yavlyaetsya opticheski tonkim i intensivnost' ego izlucheniya vsegda men'she ravnovesnoi v $a'_\nu x_0$ raz. Polnyi potok energii, izluchaemoi takimi oblakami, proporcionalen $F=\int F_\nu d\nu= x_o\,\int a'_\nu F_{\nu\;\rm eq}d\nu$ . Vvedem srednii koefficient poglosheniya

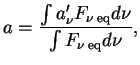
$\displaystyle a={\int a'_\nu F_{\nu\;\rm eq}d\nu\over \int F_{\nu\;\rm eq}d\nu},$

togda

$\displaystyle F=ax_0F_{eq}.$

Srednii koefficient poglosheniya dlya tormoznogo mehanizma, ochevidno, raven

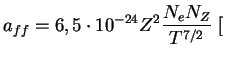$\displaystyle a_{ff}=6,5\cdot 10^{-24}Z^2{N_eN_Z\over T^{7/2}}\;[$ sm $\displaystyle ^{-1}].$

Sootvetstvuyushaya srednyaya dlina svobodnogo probega fotona

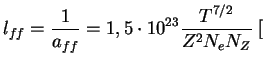$\displaystyle l_{ff}={1\over a_{ff}}=1,5\cdot 10^{23}{T^{7/2}\over Z^2N_eN_Z}\;[$ sm $\displaystyle ].$

Prichem, esli plazma soderzhit smes' ionov s zaryadami

i atomnymi massami

, to

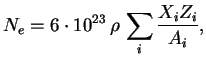
$\displaystyle N_e=6\cdot 10^{23}\,\rho\,\sum\limits_i{X_iZ_i\over A_i},$

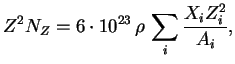
$\displaystyle Z^2N_Z=6\cdot 10^{23}\,\rho\,\sum\limits_i{X_iZ_i^2\over A_i},$

gde

-- vesovaya dolya dannogo iona.

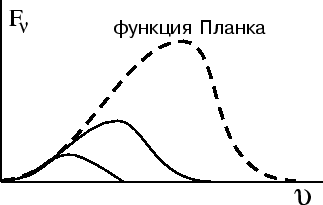
$\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f19.ai}\hss} \end{wrapfigure}$

Ris. 19.

Rassmotrim process ustanovleniya ravnovesiya mezhdu veshestvom i izlucheniem dlya odnorodnoi neogranichennoi sredy, v kotoroi v nachal'nyi moment izluchenie otsutstvovalo, a veshestvo bylo mgnovenno nagreto do temperatury . Ochevidno, chto prezhde vsego eto ravnovesie ustanovitsya na nizkih chastotah, tak kak $a'_\nu\sim 1/\nu^2$ . S techeniem vremeni ravnovesie budet ustanavlivat'sya pri bol'shih znacheniyah $\nu$ (sm. ris. 19).

<< 3.3 Kinetika fotonov i | Oglavlenie | 3.5 Rasseyanie izlucheniya na ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce