Astronet > 3.5 Rasseyanie izlucheniya na svobodnyh elektronah

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 3.4 Tormoznoe izluchenie zaryadov | Oglavlenie | 4. Teoriya perenosa (prodolzhenie) >>

3.5 Rasseyanie izlucheniya na svobodnyh elektronah

Rassmotrim dvizhenie elektrona v ploskoi elektromagnitnoi volne: $E_x=E_0\,\cos \omega t$ , rasprostranyayusheisya vdol' osi . Uravnenie dvizheniya elektrona:

$\displaystyle m\ddot x=eE_0\,\cos \omega t,$

i energiya, izluchaemaya takim elektronom,

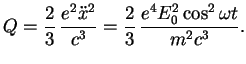
$\displaystyle Q={2\over 3}\,{e^2{\ddot x}^2\over c^3}={2\over 3}\,{e^4E_0^2\cos^2\omega t\over m^2c^3}.$

Svoih istochnikov energii u elektrona net. Fakticheski on pereizluchaet (rasseivaet) energiyu padayushei elektromagnitnoi volny v drugih napravleniyah, tak chto

$\displaystyle Q=W\sigma_T\;[$ erg $\displaystyle /$ s $\displaystyle ],$

gde $W\;[$ erg

-- potok padayushei energii:

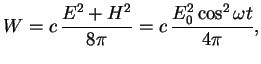
$\displaystyle W=c\,{{E^2+H^2}\over 8\pi}=c\,{E_0^2\cos^2\omega t\over 4\pi},$

i sechenie rasseyaniya

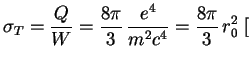$\displaystyle \sigma_T={Q\over W}={8\pi\over 3}\,{e^4\over m^2c^4}={8\pi\over 3}\,r_0^2\;[$ sm $\displaystyle ^2]$

znamenitaya formula Tomsona. Velichina

$\displaystyle r_0=e^2/mc^2=2,8\cdot 10^{-13}\;$ sm $\displaystyle$

nazyvaetsya klassicheskim radiusom elektrona.

Pri preobladayushei roli elektronnogo rasseyaniya (processy poglosheniya izlucheniya nesushestvenny) izmenenie intensivnosti $F_\nu$ v monohromaticheskom puchke fotonov, ochevidno, ravno

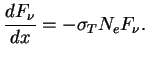
$\displaystyle {dF_\nu\over dx}=-\sigma_TN_eF_\nu.$

Mozhno vvesti koefficient ``poglosheniya'' pri tomsonovskom rasseyanii (hotya real'no poglosheniya energii i net):

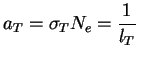$\displaystyle a_T=\sigma_TN_e={1\over l_T}\;$ sm $\displaystyle ^{-1},$

gde dlina probega

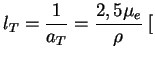$\displaystyle l_T={1\over a_T}={2,5\mu_e\over \rho}\;[$ sm $\displaystyle ].$

Integriruya uravnenie dlya $F_\nu$ , poluchaem

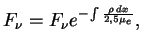
$\displaystyle F_\nu=F_\nu e^{-\int {\rho\,dx\over 2,5\mu_e}},$

t.e. $2,5\;$ g/sm

vodorodnoi plazmy ( $\mu_e=1$ ) umen'shayut $F_\nu$ v

raz za schet elektronnogo rasseyaniya.

V astrofizike obychno pol'zuyutsya ne koefficientom poglosheniya $a_T,\;a_\nu$ , a tak nazyvaemoi neprozrachnost'yu

$\displaystyle \kappa_\nu=a_\nu/\rho\;[$ sm $\displaystyle ^2/$ g $\displaystyle ].$

Takim obrazom, neprozrachnost' za schet rasseyaniya

$\displaystyle \kappa_T=0,4\mu_e\;[$ sm $\displaystyle ^2/$ g $\displaystyle ].$

Z a d a ch i. 1. Dana vodorodnaya () plazma so znacheniyami plotnosti $\rho=10^{-6},\;10^{-3},\;1\;$ gsm, temperaturoi $T=10^8,\;3\cdot 10^6,\;10^5\;$ K. Dlya $x=h\nu/kT=10^{-2},\;10^{-1},\;1,\;5,\;20$ naiti $\nu,\; \lambda,\;\kappa_{f\!f},\;\kappa_T$ . V peremennyh $\lg T-\lg \rho$ naiti krivuyu, na kotoroi $\kappa_{f\!f}=\kappa_T$ . Podschitaite $J_\nu$ .

2. Pust' v kazhdoi tochke zvezdy plotnost' i temperatura svyazany sootnosheniem $\rho=$ const $\cdot T^3$ , gde const zaranee ne izvestna. (Togda $P\sim T^4\sim \rho^{4/3}$ , t.e. indeks politropy .) Dlya chisto vodorodnyh modelei zvezd s massami $M=1,\;10,\;100_\odot$ i central'nyh plotnostei $\rho_c=100,\;1$ i $10^{-2}\;$ $\mbox {g}/\mbox{sm}^3$ naiti radius , temperaturu v centre i polnuyu energiyu ${\cal E}$ .

3. Pust' raspredelenie plotnosti po zvezde opredelyaetsya zavisimost'yu $\rho=\rho_c {[1-(r/R)^2]}^g$ , gde $g=1,\;2,\;3$ . Naiti gravitacionnuyu energiyu zvezdy $U=-{GM^2 \over R}\,K_g$ , t.e. naiti .

Pust' energiya edinicy massy svyazana s $\rho$ sootnosheniyami: a) $E=A\rho^{1/3}\,$ , b) $E=A\rho^{1/2}$ . (Kakoe pri etom $P=P(\rho)$ ?)

Pri teh zhe raspredeleniyah plotnosti naiti svyaz' mezhdu i iz usloviya minimuma polnoi energii ${\cal E}$ .

<< 3.4 Tormoznoe izluchenie zaryadov | Oglavlenie | 4. Teoriya perenosa (prodolzhenie) >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce