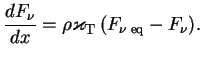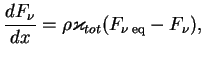Astronet > 4. Teoriya perenosa (prodolzhenie)

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 3.5 Rasseyanie izlucheniya na ... | Oglavlenie | 4.2 Koefficient teplopro... >>

4. Teoriya perenosa (prodolzhenie)

Razdely

4.1 Perenos izlucheniya pri rasseyanii

V predydushei glave bylo polucheno uravnenie dlya izmeneniya intensivnosti pri tomsonovskom rasseyanii

$\displaystyle {dF_\nu\over dx}=-\varkappa_{\mbox{\sc t}}\,\rho\,F_\nu,\;\varkappa_{\mbox{\sc t}}=0,4/\mu_e\;\left[{\mbox{sm}^2 \over\mbox{g}}\right].$

Takim obrazom, intensivnost' izlucheniya udalennogo tochechnogo istochnika pri prohozhdenii cherez rasseivayushuyu sredu umen'shaetsya. Odnako vnutri zvezd v usloviyah lokal'nogo termodinamicheskogo ravnovesiya (LTR) izluchenie idet so vseh napravlenii, tak chto hotya chast' luchei uhodit s dannogo napravleniya za schet rasseyaniya, za schet togo zhe rasseyaniya prihodyat luchi s drugih napravlenii. Poetomu uravnenie perenosa mozhno zapisat' v vide (poskol'ku chastota pri rasseyanii ne izmenyaetsya)(Sechenie rasseyaniya schitaem ne zavisyashim ot ugla, tak kak tomsonovskoe sechenie rasseyaniya simmetrichno otnositel'no rasseyaniya na ugly $\pi$ i $\pi-\Theta:\;\sigma(\Theta)=\sigma(\pi- \Theta)$ . Poetomu v teorii perenosa ego mozhno zamenit' na $\sigma=$ const.)

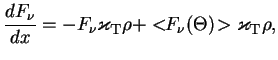
$\displaystyle {dF_\nu\over dx}=-F_\nu\varkappa_{\mbox{\sc t}}\rho+<\!\!F_\nu(\Theta)\!>\varkappa_{\mbox{\sc t}}\rho,$

gde $<\!\!F_\nu(\Theta)\!>$ -- usrednennaya po uglu intensivnost' izlucheniya.

Nas interesuet potok energii izlucheniya. Poskol'ku polnogo termodinamicheskogo ravnovesiya net, v kazhdoi tochke dolzhna byt' zavisimost' $F_\nu$ ot napravleniya (anizotropiya). Odnako eta anizotropiya vnutri zvezdy mala, i pri usrednenii po vsem napravleniyam my poluchim velichinu, malo otlichnuyu ot ravnovesnoi,

$\displaystyle <\!\!F_\nu(\Theta)\!>=F_{\nu\;\rm eq}.$

V usloviyah LTR temperatura plazmy sootvetstvuet temperature $F_{\nu\;\rm eq}$ i $F_{\nu\;\rm eq}$ yavlyaetsya v sfericheskoi zvezde funkciei tol'ko radiusa

$\displaystyle F_{\nu\;\rm eq}=F_{\nu\;\rm eq}(r).$

Poetomu pri rasseyanii uravnenie perenosa imeet tot zhe vid, chto i pri pogloshenii:

$\displaystyle {dF_\nu\over dx}=\rho\varkappa_{\mbox{\sc t}}\,(F_{\nu\;\rm eq}-F_\nu).$

(4.1)

Raznica zaklyuchaetsya v oblasti primenimosti. Dlya tormoznyh processov dostatochno tol'ko ravnovesiya plazmy, a izluchenie mozhet byt' sushestvenno neravnovesnym i uravnenie $dF_\nu/dx=\rho\varkappa (F_{\nu\;\rm eq}-F_\nu)$ primenimo dazhe vblizi kraya zvezdy. Dlya rasseyaniya izluchenie dolzhno byt' pochti ravnovesnym, poetomu u kraya zvezdy, gde sil'na anizotropiya izlucheniya, uravnenie (4.1) neprimenimo. Itak, vnutri zvezdy

$\displaystyle {dF_\nu\over dx}=\rho\varkappa_{tot}(F_{\nu\;\rm eq}-F_\nu),$

(4.2)

gde

$\displaystyle \varkappa_{tot}=\varkappa_{f\!f}+\varkappa_{\mbox{\sc t}}\,.$

V drugih usloviyah mogut igrat' rol' i drugie mehanizmy neprozrachnosti, no eti ostayutsya vazhnymi.

Kak reshat' uravnenie perenosa (4.2)? V usloviyah LTR predlagaetsya sleduyushii metod posledovatel'nyh priblizhenii.

1-e priblizhenie: $F_\nu=F_{\nu\;\rm eq}(x)$ (v opticheski tonkoi plazme $F_\nu\ll F_ {\nu\;\rm eq}$ ).

2-e priblizhenie: naidem malye otkloneniya ot polnogo termodinamicheskogo ravnovesiya. Podstavlyaya $F_{\nu\;\rm eq}(x)$ v levuyu chast' (4.2), imeem vdol' lucha s koordinatoi

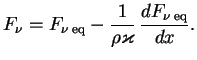
$\displaystyle F_\nu=F_{\nu\;\rm eq}-{1\over \rho\varkappa}\,{dF_{\nu\;\rm eq}\over dx}.$

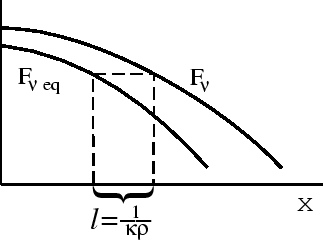
$\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f20.ai}\hss} \end{wrapfigure}$

Ris. 20.

Velichina $l=1/\varkappa\rho$ , ochevidno, est' dlina svobodnogo probega kvanta $h\nu$ . Predpolagaya, chto $F_{\nu\;\rm eq}=F_{\nu\;\rm eq}(x)$ , imeem

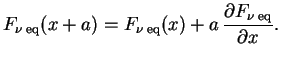
$\displaystyle F_{\nu\;\rm eq}(x+a)=F_{\nu\;\rm eq}(x)+a\,{\partial F_{\nu\;\rm eq}\over \partial x}.$

Sopostavlyaya eti dve formuly, my vidim, chto $F_\nu(x)$ est' $F_{\nu\;\rm eq}$ v tochke, ``otstayushei'' ot

na dlinu svobodnogo probega fotona (sm. ris. 20):

$\displaystyle F_\nu=F_{\nu\;\rm eq}(x-l).$

<< 3.5 Rasseyanie izlucheniya na ... | Oglavlenie | 4.2 Koefficient teplopro... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce