Astronet > 4.2 Koefficient teploprovodnosti. Rosselandovo srednee

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 4.1 Perenos izlucheniya pri ... | Oglavlenie | 4.3 Povedenie plotnosti i ... >>

4.2 Koefficient teploprovodnosti. Rosselandovo srednee

Zaimemsya vazhnoi dlya teorii zvezd zadachei -- opredelim koefficient teploprovodnosti.

$F_{\nu\;\rm eq}$ yavlyaetsya funkciei tol'ko temperatury. Pust' temperatura menyaetsya vdol' koordinaty $z,\;T=T(z),\;x$ -- lyubaya os' v prostranstve, i $\Theta$ -- ugol mezhdu osyami $(z,\;x)$ . Togda

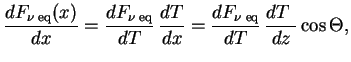
$\displaystyle {dF_{\nu\;\rm eq}(x)\over dx}={dF_{\nu\;\rm eq}\over dT}\,{dT\over dx} ={dF_{\nu\;\rm eq}\over dT}\,{dT\ \over dz}\cos \Theta,$

t.e. $dF_{\nu\;\rm eq}/dx$ zavisit ot ugla $\Theta$ , i dlya intensivnosti imeem sootnoshenie

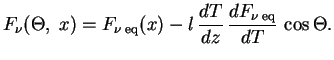
$\displaystyle F_\nu(\Theta,\;x)=F_{\nu\;\rm eq}(x)-l\,{dT\over dz}\, {dF_{\nu\;\rm eq}\over dT}\,\cos \Theta.$

Podschitaem polnyi potok energii, prointegrirovannyi po vsem chastotam. Po soobrazheniyam simmetrii potok napravlen vdol' osi

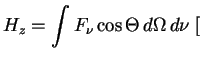$\displaystyle H_z=\int F_\nu\cos \Theta\, d\Omega\, d\nu\;[$ erg/s sm $\displaystyle ^2].$

Integral po $d \Omega$ beretsya po vsem uglam, t.e. polnyi potok est' raznost' potokov sleva napravo i sprava nalevo. Podstavim $F_\nu$ v vyrazhenie dlya

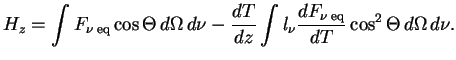
$\displaystyle H_z=\int F_{\nu\;\rm eq}\cos\Theta \,d\Omega\, d\nu-{dT\over dz}\int l_\nu{dF_{\nu\;\rm eq} \over dT}\cos^2\Theta \,d\Omega\, d\nu.$

Vezde nizhe budem pisat' $B_\nu$ , ponimaya pod etim $F_{\nu\;\rm eq}$ . Pervyi chlen v pravoi chasti uravneniya posle integrirovaniya po $d \Omega$ obrashaetsya v nol', a vo vtorom zavisimost' $\cos^2\Theta$ dast $4\pi/3$ . V itoge polnyi potok raven

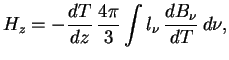
$\displaystyle H_z=-{dT\over dz}\,{4\pi\over 3}\int l_\nu\,{dB_\nu\over dT}\,d\nu,$

gde velichina ${4\pi\over 3}\int l_\nu\,{dB_\nu\over dT}\,d\nu$ nazyvaetsya koefficientom luchistoi teploprovodnosti (napomnim, chto v obshem sluchae koefficientom teploprovodnosti nazyvaetsya velichina, stoyashaya pri $\nabla T$ ). Zapishem vyrazhenie dlya

v tom zhe vide, chto i v kineticheskoi teorii gazov. Ranee my opredelili plotnost' izlucheniya v kazhdoi tochke kak

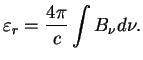
$\displaystyle \varepsilon_r={4\pi\over c}\int B_\nu d\nu.$

Sledovatel'no,

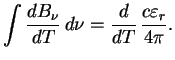
$\displaystyle \int {dB_\nu\over dT}\,d\nu={d\over dT}\,{c\varepsilon_r\over 4\pi}.$

Vvedem srednyuyu dlinu probega

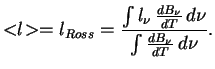
$\displaystyle <\!\!l\!>=l_{Ross}={\int l_\nu\,{dB_\nu\over dT}\,d\nu\over \int {dB_\nu\over dT}\,d\nu}.$

Eta velichina nazyvaetsya rosselandovym srednim. Togda

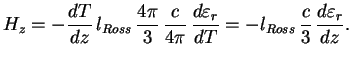
$\displaystyle H_z=-{dT\over dz}\,l_{Ross}\,{4\pi\over 3}\,{c\over 4\pi}\,{d\varepsilon_r\over dT}=-l_{Ross}\,{c\over 3}\,{d \varepsilon_r\over dz}.$

Itak, $\vec H=-D\nabla \varepsilon_r$ , gde

-- koefficient diffuzii takoi zhe, kak v kineticheskoi teorii gazov. Glavnyi vklad v rosselandovo srednee dayut kvanty s energiei $h\nu\approx 4kT$ , t.e. osnovnuyu rol' v perenose energii igrayut kvanty s bol'shoi energiei.

V opticheski tolstom tele s istochnikom tepla vnutri voznikaet gradient temperatury, i potok tepla opredelyaetsya zonami prozrachnosti. Opticheski tonkii goryachii sloi izluchaet (po zakonu Kirhgofa) to zhe, chto on pogloshal by pri vneshnem obluchenii. Takim obrazom, bol'she vsego takoi sloi izluchaet tam, gde velika neprozrachnost', naprimer v liniyah.

P r i m e r y. 1. Pust' imeetsya tol'ko tomsonovskoe rasseyanie, t.e. $l=1/ \varkappa_{\mbox{\sc t}}\rho$ . Chemu ravno $l_{Ross}$ ? Ochevidno, $l_{Ross}=l$ , tak kak ne zavisit ot $\nu$ .

Ris. 21.

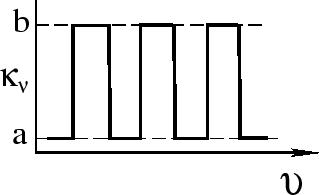
2. Pust' neprozrachnost' $\varkappa_\nu$ zadana v vide grebenki (ris. 21) s dlinoi zubcov $b-a,\;b\gg a$ i shirinoi zubcov, ravnoi rasstoyaniyu mezhdu nimi. Togda, ochevidno, $l_{Ross}\simeq 1/2a\rho$ , t.e. v zadachah perenosa izlucheniya ves' potok postupaet v ``oknah bol'shei prozrachnosti'' (otvet ne zavisit ot !). V zadachah ob izluchenii opticheski tonkoi plazmy vse opredelyaetsya verhushkami grebenki, gde veliko pogloshenie i veliko izluchenie.

V pervom priblizhenii takaya grebenka (tol'ko s razlichnoi shirinoi zubcov i promezhutkov) mozhet imitirovat' uchet poglosheniya v liniyah pri perenose izlucheniya.

3. Naidem $l_{Ross}$ dlya tormoznogo poglosheniya. Imeem

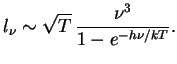
$\displaystyle l_\nu\sim\sqrt{T}\,{\nu^3\over {1-e^{-h\nu/kT}}}.$

Vvedem $x=h\nu/kT$ , togda

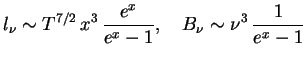
$\displaystyle l_\nu\sim T^{7/2}\,x^3\,{e^x\over {e^x-1}},\quad B_\nu\sim\nu^3\,{1\over {e^x-1}}$

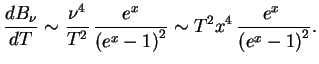
$\displaystyle {dB_\nu\over dT}\sim {\nu^4\over T^2}\,{e^x\over {(e^x-1)}^2}\sim T^2x^4\,{e^x\ \over {(e^x-1)}^2}.$

Integriruya i vypisyvaya chislennye koefficienty, poluchim

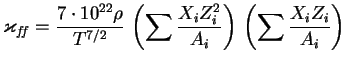
$\displaystyle \varkappa_{f\!f}={7\cdot 10^{22}\rho\over T^{7/2}}\,\left(\sum {X_iZ_i^2\over A_i} \right)\,\left(\sum {X_iZ_i\over A_i}\right)$

-- formula Kramersa.

Kak i ran'she,

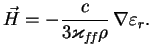
$\displaystyle \vec H=-{c\over 3\varkappa_{f\!f}\rho}\,\nabla \varepsilon_r.$

Okazyvaetsya, chto $\varkappa_{f\!f}=\varkappa_\nu$ pri $h\nu/kT=6$ , t.e. effektivnyi perenos tepla osushestvlyaetsya kvantami bol'shoi energii. Eto ob'yasnyaetsya tem, chto maksimum vesovoi funkcii $dB_\nu/dT$ prihoditsya na $x\approx 4$ , i, krome togo, tem, chto usrednyaetsya $1/a'_\nu$ , a $a'_\nu$ ubyvaet s chastotoi.

Zametim, chto v formulu dlya neprozrachnosti vhodit otnoshenie $\rho/T^{7/2}$ . S drugoi storony, kak my pokazali ranee, $\rho/T^3\sim P_g/P_r$ , prichem eto otnoshenie opredelyaetsya massoi zvezdy. Takim obrazom, v pervom priblizhenii, prenebregaya razlichiem $T^{7/2}$ i , poluchim, chto $\varkappa$ proporcional'na i tozhe odnoznachno zavisit ot massy zvezdy.

Esli v neprozrachnosti vazhny oba mehanizma, to $\varkappa_{Ross}\ne\varkappa_{f\!f}+\varkappa_{\mbox{\sc t}}$ (ne zabyvaite, chto usrednyaem $l_\nu=1/(\varkappa_\nu+\varkappa_{\mbox{\sc t}})$ ). V kachestve uprazhneniya podschitaite v etom sluchae $\varkappa_{Ross}$ . Mozhno pokazat', chto

$\displaystyle \varkappa_{Ross}=\varkappa_{\mbox{\sc t}}\,f(\rho/T^{7/2}).$

Ne nado preuvelichivat' tochnost' vseh etih raschetov. Vse, chto my govorili, spravedlivo dlya vodorodnoi plazmy, no dlya real'nogo zvezdnogo veshestva sushestvenna rol' tyazhelyh elementov. Naprimer, dlya zheleza energiya svyazi poslednih -elektronov poryadka 9 keV i stepen' ionizacii ego menyaetsya s glubinoi. Vse okazyvaetsya gorazdo slozhnei. Neobhodimo uchityvat' mnogie processy: svobodno-svyazannye, svyazanno-svyazannye (linii) i dr. V etoi knige daetsya lish' obshaya fizicheskaya kartina, obshee predstavlenie, a ne tochnye metody rascheta. Odin vopros o teploprovodnosti, rassmatrivaemyi v sovremennyh stat'yah, mozhet byt' predmetom celogo kursa. Nastoyashii kurs pozvolit nachat' chtenie original'nyh statei, no nikak ne zamenit ih.

<< 4.1 Perenos izlucheniya pri ... | Oglavlenie | 4.3 Povedenie plotnosti i ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce