Astronet > 5.3 Uchet elektromagnitnogo vzaimodeistviya chastic

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 5.2 Prosteishie primery | Oglavlenie | 5.4 Slaboe vzaimodeistvie >>

5.3 Uchet elektromagnitnogo vzaimodeistviya chastic

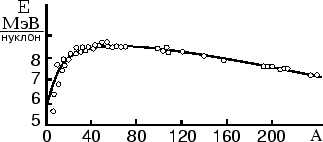
Elektromagnitnoe vzaimodeistvie igraet rol' popravki k yadernym silam -- my videli eto na primere ${}^{3}{\mathrm{He}}$ i ${}^{3}{\mathrm{T}}$ . Drugoi bolee sil'nyi primer: yadro ${}^{6}{\mathrm{He}}$ -- svyazano, no s zamenoi dvuh neitronov na dva protona, ne sushestvuet iz-za kulonovskogo ottalkivaniya. S uchetom principa Pauli naibolee kompaktno mozhno ulozhit' yadro s ravnym chislom protonov i neitronov, no iz-za kulonovskogo ottalkivaniya vygodnee brat' neskol'ko bol'she neitronov. Naprimer, $\strut_{92}^{238}$ U sostoit iz 146 neitronov i 92 protonov, t.e. neitronov v 1,5 raza bol'she. Po etoi zhe prichine tyazhelye yadra neustoichivy otnositel'no deleniya.

Bez kulonovskogo ottalkivaniya dve ``yadernye kapli'' stremilis' by slit'sya. Ob'emnye energii pri etom prosto skladyvayutsya, a poverhnostnaya -- umen'shaetsya, tak kak poverhnost' bol'shoi kapli men'she summy poverhnostei dvuh malyh. Odnako, vsledstvie togo chto kulonovskie sily spadayut po stepennomu zakonu, a yadernye -- po eksponencial'nomu, v krupnyh kaplyah (yadra s bol'shim Z) dalekie protony uzhe ne prityagivayutsya drug k drugu za schet yadernyh sil, a tol'ko ottalkivayutsya za schet kulonovskih. Takim obrazom, kulonovskaya energiya ne ochen' sushestvenna v legkih yadrah i vazhna v tyazhelyh, vsledstvie chego yadra s promezhutochnymi znacheniyami Z (Fe) naibolee prochno svyazany (sm. ris. 27).

Kolichestvennye popravki k energii -- eto odna storona dela. Drugoi vazhnyi aspekt ucheta elektromagnitnyh vzaimodeistvii -- eto processy rozhdeniya i poglosheniya fotonov:

$\displaystyle p+n\to {}^{2}{\mathrm{D}}+\gamma\;,$

$\displaystyle {}^{2}{\mathrm{D}}+p\to {}^{3}{\mathrm{He}}+\gamma\;.$

Reakciya ${}^{2}{\mathrm{D}}+{}^{2}{\mathrm{D}}\to {}^{3}{\mathrm{T}}+p$ i podobnye ei napominayut igru v kubiki -- oni svodyatsya prosto k peregruppirovke nuklonov. Zdes' zhe proishodit nechto novoe -- rozhdenie chastic (fotona ne bylo, potom on rodilsya). Iz-za zakona sohraneniya energii reakciya $p+n\to {}^{2}{\mathrm{D}}+\gamma$ ne mozhet idti bez ispuskaniya fotona. Prityazhenie protona k neitronu vsegda est', no esli nuklony sblizhayutsya i ne rozhdayut nikakoi chasticy, to energiya sohranyaetsya i oni obyazany razletet'sya.

Teper' v sechenie vzaimodeistviya $p+n={}^{}{\mathrm{D}}+\gamma$ voidet veroyatnost' rozhdeniya fotonov, t.e. poyavlyaetsya mnozhitel' $e^2/\hbar c=1/137$ . Rassmotrim process rozhdeniya fotonov na primere klassicheskogo oscillyatora. Dlya koleblyushegosya zaryada energiya, vydelyayushayasya v edinicu vremeni,

$\displaystyle Q\;\left[{\mbox{erg}\over \mbox{s}}\right]\simeq{e^2\over c^3}\, \left({d^2x\over dt^2}\right)^2={e^2r^2\,\omega^4 \over c^3}\;.$

Vremya izlucheniya odnogo kvanta $\hbar\omega$

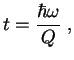
$\displaystyle t={\hbar\omega\over Q}\;,$

a veroyatnost' etogo processa $W\sim 1/t$ , takim obrazom, ravna

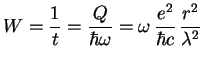
$\displaystyle W={1\over t}={Q\over \hbar\omega}=\omega\,{e^2\over \hbar c}\,{r^2\over \lambda^2}$

(zdes' $\lambda=c/\omega$ ).

Po poryadku velichiny eto vyrazhenie goditsya dlya lyuboi sistemy i veroyatnost' yadernyh prevrashenii s uchetom elektromagnitnogo vzaimodeistviya

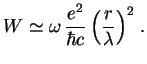
$\displaystyle W\simeq\omega\,{e^2\over \hbar c}\,{\left({r\over \lambda}\right)}^2\;.$

Dlya prostoi peregruppirovki veroyatnost' $W\sim 1/t\sim\omega$ . Teper' vhodyat bezrazmernye velichiny $e^2/\hbar c$ -- sila vzaimodeistviya i ${(r/\lambda)}^2$ -- otnoshenie ploshadi ``antenny'' k kvadratu dliny volny. Eto verno pri dipol'nyh kolebaniyah. Esli kolebaniya imeyut druguyu mul'tipol'nost', to vhodyat bolee vysokie stepeni $( r/\lambda)$ .

Z a d a ch a. Izvestno sechenie reakcii $n+p\to D+\gamma$ ,

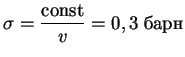
$\displaystyle \sigma={\mbox{const}\over v}=0,3\;\mbox{barn}$

pri $v=2,7\cdot 10^5$ sm/s (takaya skorost' sootvetstvuet skorosti neitronov pri komnatnoi temperature). Pri vysokoi temperature, kogda est' fotony s energiei bol'she 2,2 MeV, ochevidno, budet proishodit' i obratnyi process fotodissociacii deiteriya, i izmenenie koncentracii deiteriya so vremenem opisyvaetsya uravneniem

$\displaystyle {d[\mathrm{D}]\over dt}=\sigma v\,[n]\,[p]-f\,(T)\,[\mathrm{D}]\;,$

zdes' $[\mathrm{D}]$ -- koncentraciya D,

-- nekotoraya funkciya. V termodinamicheskom ravnovesii $\frac{d[\mathrm{D}]}{dt}=0$ i

$\displaystyle {[n]\,[p]\over [\mathrm{D}]}=F(T)\,\exp(-2,2\,$ MeV $\displaystyle /kT)\;.$

Naiti funkcii

i sechenie fotodissociacii deiteriya v zavisimosti ot temperatury.

(U k a z a n i e: prenebrech' edinicei v formule Planka, t.e. schitat' ${(e^ x-1)}^{-1}\simeq e^{-x}$ ).

<< 5.2 Prosteishie primery | Oglavlenie | 5.4 Slaboe vzaimodeistvie >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce