Astronet > 5.4 Slaboe vzaimodeistvie

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 5.3 Uchet elektromagnitnogo ... | Oglavlenie | 5.5 Yadernye reakcii v ... >>

5.4 Slaboe vzaimodeistvie

Tipichnyi primer slabogo vzaimodeistviya -- prevrashenie neitrona v proton s ispuskaniem elektrona i antineitrino $\widetilde \nu$ :

$\displaystyle n\to p+e^-+\widetilde \nu\;.$

Vzaimodeistvie nazyvaetsya slabym iz-za maloi skorosti raspada. Vremya zhizni svobodnogo neitrona poryadka 10 min. Vyshe my rassmatrivali reakcii s harakternymi vremenami $10^{-22}$ s dlya chisto yadernogo vzaimodeistviya i $10^{-16}$ s uchastiem elektromagnitnogo vzaimodeistviya, t.e. s ispuskaniem $\gamma$ -kvantov.

Podcherknem, chto pri slabyh vzaimodeistviyah, kak i pri elektromagnitnyh, reakcii idut s rozhdeniem novyh chastic, t.e. chislo chastic ne sohranyaetsya. Ni v koem sluchae nel'zya schitat', chto i $\widetilde \nu$ ``sidyat'' v neitrone, chto neitron est' svyazannaya sistema iz protona i elektrona. Neitron tak zhe elementaren, kak i proton^5.2. Chasticy deistvitel'no rozhdayutsya. Zdes' mozhno provesti analogiyu so zvukom: kosnemsya struny -- rozhdayutsya fonony.

V reakciyah takogo roda mozhno perenosit' chasticu sprava nalevo i sleva napravo (s obyazatel'noi zamenoi chasticy na antichasticu):

$\displaystyle e^++n\rightleftarrows p+\widetilde \nu\,,$

$\displaystyle \nu+n\rightleftarrows p+e^-\,,$

$\displaystyle p\rightleftarrows n+e^++\nu\,.$

Chem otlichaetsya antineitrino $\widetilde \nu$ ot neitrino $\nu$ ? Dlya $\nu$ i $\widetilde \nu$ massa pokoya , zaryad i, kazalos' by, razlichii mezhdu nimi net. Otlichayutsya oni po tipu reakcii, v kotoryh uchastvuyut. Naprimer, vblizi reaktora eksperimental'no nablyudalas' reakciya $\widetilde \nu+p\to n+e^+$ i net reakcii $\nu+n\to p+e^-$ , tak kak reaktor daet tol'ko antineitrino. Esli by eti chasticy byli tozhdestvenny (kak foton i antifoton), to nichto ne meshalo by poluchit' reakciyu $\nu+n\to p+e^-$ . Tak zhe po tipu reakcii bylo otkryto, chto neitrino byvayut dvuh sortov: neitrino elektronnoe $\nu_e$ i neitrino myuonnoe $\nu_\mu$ . Poslednie uchastvuyut v reakciyah tipa

$\displaystyle p+\mu^-\to n+\nu_\mu\;,$

gde $\mu^-$ -- myu-mezon^5.3.

Sleduyushii vazhnyi moment slabyh vzaimodeistvii: kak ponimat' reakciyu $p\to n+e^+ +\nu$ ? Ved' proton stabilen. My pisali reakcii tol'ko s uchetom zakonov sohraneniya zaryadov. No nuzhno takzhe udovletvorit' eshe i zakonu sohraneniya energii. Odnako sohranenie zaryada -- absolyutno, a na energiyu sistemy mozhno vozdeistvovat' izvne.

Massa neitrona ravna

$\displaystyle m_n=M_{\rm H}+0,78 \;$ MeV $\displaystyle =m_p+m_e+0,78 \;$ MeV $\displaystyle \;,$

Ris. 28.

gde $M_{\rm H}$ -- massa atoma vodoroda (yasno, chto $M_{\rm H}=m_p+m_e$ , poskol'ku energiei svyazi elektrona v atome vodoroda $\sim$ 13,6 eV mozhno prenebrech'). Poetomu reakciya $p\to n+e^+ +\nu$ v svobodnom sostoyanii idti ne mozhet -- ne hvataet energii. No voz'mem svyazannye i v sistemah: ${}^{13}{\mathrm{C}}={}^{12}{\mathrm{C}}+n$ i ${}^{13}{\mathrm{N}}={}^{12}{\mathrm{C}}+p$ (sm. ris. 28). Po yadernym silam ${}^{12}{\mathrm{C}}$ odinakovo vzaimodeistvuet kak s , tak i s , no kulonovskoe ottalkivanie umen'shaet energiyu svyazi protona. Svyazannyi v yadre ${}^{12}{\mathrm{C}}$ proton $p_{bound}$ okazalsya ``tyazhelee'' svyazannogo neitrona, poetomu mozhet idti reakciya ${}^{13}{\mathrm{N}}\to {}^{13}{\mathrm{C}}+e^+ +\nu$ , t.e.

$\displaystyle p_{bound}\to n_{bound} +e^+ +\nu\;.$

Stabil'nost' protona i nestabil'nost' neitrona v nekotorom smysle uslovny, tak kak v svyazannom sostoyanii stabil'nym mozhet okazat'sya neitron, a ne proton.

Poidet li reakciya $p+e^-\to n+\nu$ ? Ved' i neitron dolzhen raspadat'sya. V silu etogo neravenstva reakciya ne poidet ni v atome vodoroda, ni v plazme maloi plotnosti i temperatury: $\rho <10^4\;$ $\mbox {g/sm}^3$ , K. Odnako reakciya poidet libo v sluchae, kogda neitron sil'no svyazan, libo kogda elektron imeet bol'shuyu energiyu. Tipichnyi primer: ${}^{7}{\mathrm{Be}}+e^-={}^{7}{\mathrm{Li}}+\nu$ , neitron v Li krepko svyazan. Bol'shaya energiya elektronov mozhet byt' obuslovlena libo vysokoi temperaturoi, libo ih vyrozhdeniem pri bol'shoi plotnosti. Naprimer, v vyrozhdennom gaze pri vysokom davlenii reakciya $p+e^-\to n+\nu$ idet pri fermi-energii elektronov $E_f>0,78\;$ MeV. V etom sluchae eta reakciya nosit nazvanie reakcii neitronizacii veshestva -- glavnyi moment v teorii pul'sarov i neitronnyh zvezd.

Takie reakcii mogli by idti i v goryachei plazme, kogda energiya elektronov dostatochno vysoka: no tam est' bolee effektivnye reakcii s ispuskaniem $\gamma$ -kvantov, kotorye bystro otnimayut energiyu u elektronov. Poetomu v razrezhennoi plazme neitronizaciya prenebrezhima iz-za slabosti vzaimodeistviya. K tomu zhe neitron raspadaetsya obratno na proton i elektron (s obrazovaniem $\widetilde \nu$ ). Interesno zametit', chto v toi zhe goryachei plazme, kogda vyhod izlucheniya iz sistemy zatrudnen (bol'shaya neprozrachnost' veshestva), processy slabogo vzaimodeistviya s obrazovaniem neitrona i ih raspadom mogut effektivno otvodit' energiyu cherez ispuskanie $\nu$ i $\widetilde \nu$ (tak nazyvaemye urka-processy, sm. razdel 7.4).

Slabye vzaimodeistviya nazyvayutsya chetyrehfermionnymi, tak kak v reakciyah uchastvuyut 4 fermi-chasticy so spinom .

Veroyatnost' vzaimoprevrasheniya chastic za schet slabogo vzaimodeistviya po analogii s teoriei elektromagnitnogo izlucheniya zapisyvaetsya v vide

$\displaystyle W={2\pi \over \hbar}\; \vert H'\vert^2{dN \over dE}\;\left[c^{-1}\right]\;,$

gde

-- chislo konechnyh sostoyanii na edinichnyi interval energii, a

-- matrichnyi element gamil'toniana vzaimodeistviya, opredelyayushii, takim obrazom, kompleksnuyu amplitudu veroyatnosti processa. V prosteishei teorii slabyh vzaimodeistvii polagayut, chto

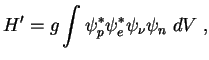
$\displaystyle H'=g\int\psi^*_p \psi^*_e \psi_{\nu}\psi_n \;dV\;,$

gde

-- postoyannaya slabogo vzaimodeistviya, a $\psi_n$ , $\psi_p$ , $\psi_e$ , $\psi_{\nu}$ -- volnovye funkcii chastic. V eto vyrazhenie neobhodimo podstavlyat' $\psi$ ili $\psi^*$ (sopryazhennuyu volnovuyu funkciyu) sootvetstvenno tomu, unichtozhaetsya ili rozhdaetsya chastica. Vyrazhenie

napisano dlya raspada neitrona $n\to p+e^-+\widetilde \nu_e$ , poetomu my pishem $\psi^*_p,\;\psi_e^*$ . Volnovaya funkciya neitrino $\psi_{\nu}$ pishetsya bez zvezdochki, tak kak rozhdenie antineitrino $\widetilde \nu_e$ ekvivalentno unichtozheniyu $\nu_e$ . Vazhnyi moment -- razmernost'

. Tak kak razmernost'

erg, a $\int\psi^2dV=1$ , t.e. $[\psi]=$ cm $^{-3/2}$ , to

erg $\cdot$ sm

. Zametim, chto konstanta elektromagnitnogo vzaimodeistviya

bezrazmerna. V sisteme CGS chislenno $g=1,4\cdot10^{-49}\;$ erg $\cdot$ sm

. Znaya

(iz opyta), mozhno opredelit' veroyatnost' raspada $n\to p+e^-+\widetilde \nu$ . Pust' energii vydelilos' mnogo, togda elektron

-- relyativistskii, i

ne dolzhna vhodit' v otvet. Veroyatnost'

proporcional'na kvadratu matrichnogo elementa, t.e. proporcional'na

. Neobhodimo podobrat' takuyu kombinaciyu stepenei

, $\hbar$ i

, chtoby poluchit' razmernost' $[W]=c^{-1}$ :

$\displaystyle W\sim\;g^2E^n\;\hbar^m\;c^p\;,$

t.e.

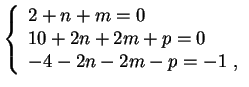
$\displaystyle \left\{\begin{array}{l} 2+n+m=0 \\ 10+2n+2m+p=0 \\ -4-2n-2m-p=-1\;, \end{array}\right.$

otkuda $n=5,\;m=-7,\;p=-6$ .

Tochnaya formula imeet vid

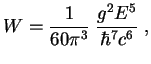
$\displaystyle W={1 \over {60\pi ^3}}\;{g^2E^5\over {\hbar ^7 c^6}}\;,$

gde koefficient $1/60\pi^3$ poluchen iz konkretnogo rascheta.

Z a d a ch a 1. Rassmotrim reakciyu

$\displaystyle e^-+p\to n+\nu\;.$

Pust' energiya elektronov $5\,$ MeV $<E_e<100\,$ MeV. Togda proton i neitron mozhno schitat' pokoyashimisya. Postroit' po razmernosti vyrazhenie dlya $\sigma[$ $\mbox {sm}^2]$ :

$\displaystyle \sigma (E) \sim g^2E^n\hbar ^mc^p\;.$

Z a d a ch a 2. Naiti veroyatnost' neitronizacii v vyrozhdennom gaze relyativistskih elektronov

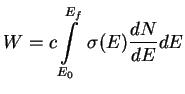
$\displaystyle W=c\int\limits^{E_f}_{E_0}\;\sigma (E){dN\over {dE}}dE$

(

-- porogovaya energiya neitronizacii).

<< 5.3 Uchet elektromagnitnogo ... | Oglavlenie | 5.5 Yadernye reakcii v ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce