Astronet > 5.5 Yadernye reakcii v zvezdah

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 5.4 Slaboe vzaimodeistvie | Oglavlenie | 5.6 Poiski solnechnyh neitrino >>

5.5 Yadernye reakcii v zvezdah

Einshteinovskoe sootnoshenie mezhdu massoi i energiei veshestva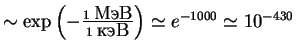

pokazyvaet, chto yadernye reakcii mogut byt' istochnikom energii zvezd. V samom dele, massa chetyreh protonov bol'she massy yadra geliya: $4m_p>m_{\rm He}$ , i obrazovanie poslednego v rezul'tate sliyaniya chetyreh protonov dolzhno proishodit' s ogromnym vydeleniem energii, ravnym raznosti massy -- defektu mass $\Delta E=(4m_p-m_{\rm He})c^2$ . Odnako dolgoe vremya do poyavleniya kvantovoi mehaniki kazalos', chto temperatura veshestva v centre zvezdy, $T\sim GM/({\cal R}R)\sim 1\;$ keV, slishkom nizka. Dlya preodoleniya kulonovskogo ottalkivaniya pri stolknovenii dvuh protonov neobhodima energiya poryadka 1 MeV. Pri maksvellovskom raspredelenii s temperaturoi $\sim$ 1 keV energiei v 1 MeV obladaet dolya chastic $\sim\exp\left(-{1\;\mbox{MeV}\over{1\; \mbox{keV}}}\right)\simeq e^{-1000}\simeq 10^{-430}$ (otmetim, chto v Solnce vsego $10^{57}$ chastic, t.e. klassicheskaya veroyatnost' vzaimodeistviya dvuh protonov nichtozhna). Tem ne menee odin iz osnovatelei teorii vnutrennego stroeniya zvezd A. Eddington, pervyi ukazavshii na vozmozhnost' reakcii $\mathrm{H}\to{}^{4}{\mathrm{He}}$ , ne sdavalsya, kogda emu ukazyvali na maluyu veroyatnost' iz-za nedostatochno vysokoi temperatury, i govoril: ``Poishite-ka mesto pogoryachee!''.

S razvitiem kvantovoi mehaniki stalo yasno, chto Eddington prav! Veroyatnost' yadernyh reakcii uvelichivaetsya blagodarya podbar'ernomu perehodu (tunnel'nyi effekt).

Ocenim skorost' yadernyh reakcii s uchetom zakonov kvantovoi mehaniki. Napomnim izvestnoe sootnoshenie De Broilya, svyazyvayushee dlinu volny $\lambda$ (volnovoe chislo $k=2\pi/ \lambda$ ) i impul's chasticy : $k=p/\hbar$ . Dvizheniyu s impul'som sootvetstvuet volnovaya funkciya $e^{ikx}\to e^{{ipx\over \hbar}}$ ili $e^{{i\over\hbar}\int pdx}$ , esli yavlyaetsya funkciei koordinat. Dlya chastic s massoi pokoya impul's naidem iz zakona sohraneniya energii

$\displaystyle p^2/(2m)=E_{\mbox{kin}}=E_{\mbox{poln}}-U=E_0-U\;.$

Otsyuda

$\displaystyle p=\sqrt{2m(E_0-U)}\;.$

Dlya dvuh chastic s zaryadami

energiya ottalkivaniya

$\displaystyle U=Z_1Z_2e^2/r\;.$

V klassicheskoi mehanike chastica s energiei

pri dostizhenii tochki

, gde

, t.e.

, povorachivaet i dvizhetsya v obratnuyu storonu. V kvantovoi teorii pri $r<r_1\;p=i\sqrt{2m(U-E_0)}$ , i v volnovuyu funkciyu chasticy, idushei s beskonechnosti, voidet mnozhitel'

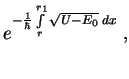
$\displaystyle e^{-{1\over\hbar}\int\limits_r^{r_1}\sqrt{U-E_0}\;dx}\;,$

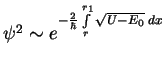t.e. sushestvuet konechnaya veroyatnost' $\psi^2\sim e^{-{2\over\hbar}\int\limits_r^{r_1} \sqrt{U-E_0}\;dx}$ prohozhdeniya chasticy v oblast'

(sm. ris. 29).

Rassmotrim integral

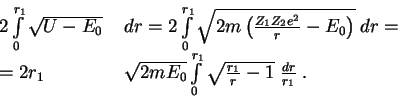
$\begin{displaymath} \begin{array}{ll} 2\int\limits_0^{r_1}\sqrt{U-E_0}\;&dr=2\in... ...{r_1}\sqrt{{r_1\over {r}}-1}\;{dr\over{r_1}}\;. \cr \end{array}\end{displaymath}$

Pust'

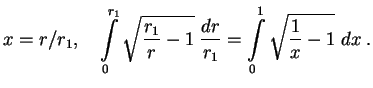
$\displaystyle x=r/r_1,\quad \int\limits_0^{r_1}\sqrt{{r_1\over {r}}-1}\;{dr\over{r_1}}=\int\limits_0^1\sqrt{{1\over{x}} -1}\;dx\;.$

Pri $x\to 0$ podyntegral'noe vyrazhenie $\to \infty$ , odnako integral shoditsya:

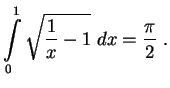
$\displaystyle \int\limits_0^1\sqrt{{1\over{x}}-1}\;dx={\pi \over 2}\;.$

Otmetim, chto shodimost' integrala pozvolyaet nam vesti integrirovanie ot nulya, a ne ot radiusa yadernogo vzaimodeistviya

, kotoryi sostavlyaet $\sim 10^{-3}r_1$ . Yasno, chto takoe priblizhenie (zamena $r_2\to 0$ ) dast lish' nebol'shoi popravochnyi mnozhitel'.

Pri tochnom vychislenii veroyatnosti pered eksponentoi est' eshe stepennye mnozhiteli, kotorye my ne uchityvaem. Dlya nas seichas vazhna tol'ko eksponenta.

Itak, $\psi^2(0)=e^{-\varphi}$ , gde

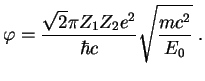
$\displaystyle \varphi={\sqrt{2}\pi Z_1Z_2e^2\over{\hbar c}}\sqrt{{mc^2\over{E_0}}}\;.$


Ris. 29.	Ris. 30.

Vyshe predpolagalos', chto odno iz yader pokoitsya ( $m_2=\infty$ ). Na samom dele pri raschete v sisteme centra mass vmesto sleduet, kak obychno, podstavit' privedennuyu massu $\mu={m_1m_2\over{m_1+m_2}}$ . Togda

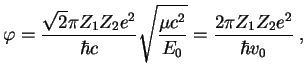
$\displaystyle \varphi={\sqrt{2}\pi Z_1Z_2e^2\over{\hbar c}}\sqrt{{\mu c^2\over{E_0}}}={2\pi Z_1Z_2e^2 \over{\hbar v_0}}\;,$

gde

-- otnositel'naya skorost' chastic na beskonechnosti. V takom vide vidna bezrazmernost' $\varphi$ (analogichno $e^2/(\hbar c)$ ).

My poluchili veroyatnost' podbar'ernogo sblizheniya chastic s dannoi energiei : $\sim e^{-\sqrt{{A\over{E_0}}}}$ , gde $A={2\pi^2Z_1^2Z_2^2e^4\over{\hbar^2}}\cdot {A_1A_2\over{A_1+A_2}}m_u\;$ (, -- atomnye massy yader). V teplovom ravnovesii (pri temperature ) kolichestvo chastic s energiei proporcional'no $e^{-{E_0\over{T}}}$ i polnaya veroyatnost'

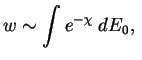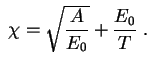
$\displaystyle w\sim\int e^{-\chi}\;dE_0,\;$ gde $\displaystyle \;\chi=\sqrt{{A\over{E_0}}}+{E_0\over{T}}\;.$

Funkciya $\chi(E_0)$ imeet minimum pri nekotorom znachenii $E_{0\,\min}$ (sm. ris. 30). Ochevidno, chto oblast' minimuma dast glavnyi vklad v integral, tak kak $e^{-\chi}$ v etoi tochke imeet ostryi maksimum. Vychislenie takih integralov provoditsya metodom perevala. Snachala nahodim ekstremum:

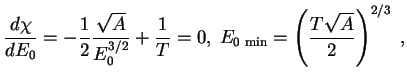
$\displaystyle {d\chi\over{dE_0}}=-{1\over2}{\sqrt{A}\over{E_0^{3/2}}}+{1\over T}=0,\;E_{0\,\min}=\left( {T\sqrt{A}\over 2}\right)^{2/3}\;,$

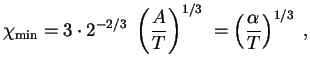
$\displaystyle \chi_{\min}=3\cdot 2^{-2/3}\;\left({A\over T}\right)^ {1/3}\;=\left({\alpha\over T}\right)^{1/3}\;,$

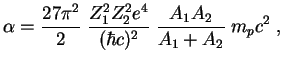
$\displaystyle \alpha={27\pi^2\over2}\;{Z_1^2Z_2^2e^4 \over{(\hbar c)^2}}\;{A_1A_2\over{A_1+A_2}}\;m_pc^2\;,$

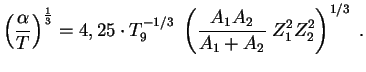
$\displaystyle \left({\alpha\over T}\right)^ {1\over3}=4,25\cdot T_9^{-1/3}\;\left({A_1A_2\over{A_1+A_2}}\;Z_1^2Z_2^2\right)^{1/3}\;.$

Zdes'

K -- temperatura v mlrd. gradusov. Teper' mozhno razlozhit' $\chi(E_0)$ v ryad Teilora v okrestnosti tochki $E_{0\,\min}$ :

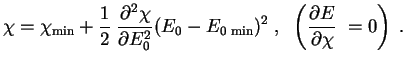
$\displaystyle \chi=\chi_{\min}+{1\over2}\;{\partial^2\chi\over\partial E_0^2}(E_0-E_{0\,\min})^2 \;,\;\;\left({\partial E\over\partial\chi}\;=0\right)\;.$

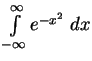Itak, $w =e^{-\chi_{\min}}$ s nekotorym mnozhitelem, poluchayushimsya ot integrirovaniya vtorogo chlena, kotoroe svoditsya k integralu vida $\int\limits_{-\infty}^{\infty}e^{-x^2}\;dx$ (provedite eto integrirovanie!). Tak my nashli tol'ko veroyatnost' sblizheniya yader. Polnaya veroyatnost' reakcii poluchitsya posle umnozheniya na veroyatnost' sootvetstvuyushego vzaimodeistviya.

Pereidem k konkretnym reakciyam.

$\displaystyle 1)\quad p+p=\mathrm{D}+e^++\nu.$

Vydelenie energii v etoi reakcii $Q=1,442\;$ MeV, v tom chisle $\sim0,25\;$ MeV unosyat neitrino.

Chislo yader deiteriya D, rozhdayushihsya v 1 sm na 1 s, ravno

$\displaystyle {d[\mathrm{D}]\over{dt}}={1\over2}\;{n^2_p\over{6\cdot 10^{23}}}\... ...{-15}T^{-2/3} _9e^{-3,38/T_9^{1/3}}\left[\mbox{s}^{-1}\,\mbox{sm}^{-3}\right].$

Vvodya vesovye doli dlya himicheskih elementov

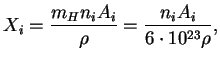
$\displaystyle X_i={m_Hn_iA_i\over{\rho}}={n_iA_i\over{6\cdot 10^{23}\rho}},$

poluchim

$\displaystyle {dX_{\rm D}\over{dt}}=4,2\cdot 10^{-15}\rho X_{\rm H}^2T^{-2/3}_9e^{-3,38/T_9^{1/3}} \left[\mbox{s}^{-1}\right].$

$\displaystyle 2)\quad \mathrm{D}+p\to {}^{3}{\mathrm{He}}+\gamma,\quad Q=5,494\;$ MeV $\displaystyle ,$

$\displaystyle {dX_{{}^{3}\mathrm{He}}\over{dt}}=3,98\cdot 10^3\cdot X_{\rm H}X_{\rm D}\rho T^{-2/3}_9e^{-3,72/T_9^{1/3}}\left[\mbox{s}^{-1}\right].$

Ukazhem na bol'shuyu raznicu (10 $^{18}$ raz) v otnoshenii koefficientov v pervoi i vo vtoroi reakcii. Eto ob'yasnyaetsya tem, chto pervaya reakciya idet so slabym vzaimodeistviem na letu, a vo vtoroi vse opredelyaetsya elektromagnitnym vzaimodeistviem. Otmetim takzhe, chto vtoraya reakciya v usloviyah zemnyh morei i okeanov ``zarezaetsya'' eksponentoi, nesmotrya na bol'shoi mnozhitel', stoyashii pered nei.

$\displaystyle 3)\quad {}^{3}{\mathrm{He}}+{}^{3}{\mathrm{He}}\to {}^{4}{\mathrm{He}}+2p,\quad Q=12,86\;$ MeV $\displaystyle .$

Skorost' reakcii:

$\displaystyle {dX_{{}^4\mathrm{He}}\over{dt}}=1,3\cdot 10^{10}\rho X_{{}^3\mathrm{He}}^2T^{-2/3}_9 e^{-{12,28\over{T_9^{1/3}}}}\left[\mbox{c}^{-1}\right].$

Zdes' mnozhitel' eshe bol'she, tak kak reakciya idet po sil'nomu vzaimodeistviyu.

Itak, my vidim, chto blagodarya cepochke reakcii 1), 2), 3) vozmozhno prevrashenie chetyreh yader vodoroda v yadro geliya s vydeleniem energii $(m_{\rm He}^4-4m_{\rm H})c^2$ . Eta cepochka reakcii mozhet idti pri dostatochno vysokoi temperature v absolyutno chistom vodorode i nazyvaetsya proton-protonnym (ili -) ciklom. Vozmozhny i drugie cepochki proton-protonnogo cikla.

Raschet pokazyvaet, chto pri nizkih temperatura $(T<2\cdot 10^7$ K reakcii idut v osnovnom po dvum sleduyushim shemam:

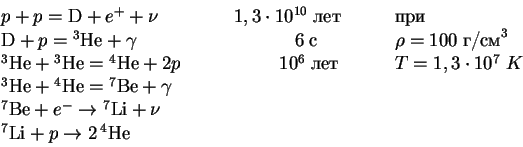
$\begin{displaymath} \begin{array}{lcl} %% zdes' !!!!!!!!!!! p+p=\mathrm{D}+e^++\... ... {}^{7}{\mathrm{Li}}+p\to 2\, {}^{4}{\mathrm{He}} \end{array}\end{displaymath}$

Sprava ukazano harakternoe vremya reakcii (kak ono vychisleno?).

Yasno, chto bez uchastiya slabogo vzaimodeistviya vodorod v He ne prevratit', tak kak iz protonov nado poluchit' neitrony. svobodnyi proton v neitron ne prevrashaetsya -- eto vozmozhno tol'ko v pole drugogo protona, kotoryi ego podhvatyvaet. Na odno yadro ${}^{4}{\mathrm{He}}$ dolzhno proiti dve reakcii $p+p\to \mathrm{D}+e^++\nu$ . Na kazhduyu reakciyu vo vsem -cikle vydelyaetsya 13,086 MeV energii.

Vtoraya cepochka interesna potomu, chto daet pobochnye produkty:

$\displaystyle {}^{7}{\mathrm{Be}}+p\to {}^{8}{\mathrm{B}}+\gamma,$

$\displaystyle {}^{8}{\mathrm{B}}\to {}^{8}{\mathrm{Be}}+e^++\nu.$

Poslednii raspad zamechatelen tem, chto on daet neitrino vysokoi energiei, v srednem

-9 MeV, kotorye mozhno detektirovat' na Zemle (sm. nizhe).

Ochevidno, chto skorost' vydeleniya energii v -cikle ravna skorosti, s kotoroi idet pervaya reakciya:

$\displaystyle p+p=\mathrm{D}+e^++\nu.$

Deiterii tut zhe vstupaet v reakciyu s protonom. Poetomu on ne nakaplivaetsya i stacionarnaya koncentraciya

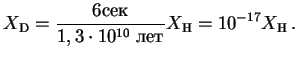
$\displaystyle X_{\rm D}={6\mbox{sek}\over{1,3\cdot10^{10}\;\mbox{let}}}X_{\rm H}=10^{-17}X_{\rm H}\,.$

Vypishem polnuyu skorost' energovydeleniya v

-cikle:

$\displaystyle \varepsilon_{pp}=\rho X_{\rm H}^2\;\varepsilon_0(T/T_0)^n\;[$ erg/(g $\displaystyle \cdot$ c) $\displaystyle ]$

	$\varepsilon_0$
1	$4\cdot 10^{-9}$	10,6
5	$1,8\cdot10^{-3}$	5,95
10	$6,8\cdot10^{-2}$	4,60
15	0,377	3,95
20	1,09	3,64
30	4,01	3,03

Pri temperaturah bolee vysokih, chem solnechnye (v bolee massivnyh zvezdah), idet CNO-cikl (on vozmozhen tol'ko v prisutstvii katalizatora ugleroda)

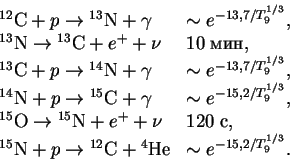
$\begin{displaymath} \begin{array}{ll} {}^{12}{\mathrm{C}}+p\to{}^{13}{\mathrm{N}... ...{C}}+{}^{4}{\mathrm{He}}& \sim e^{-15,2/T_9^{1/3}}. \end{array}\end{displaymath}$

Obratite vnimanie na to, chto v poslednei reakcii snova obrazuetsya yadro ${}^{12}{\mathrm{C}}$ , s kotorogo nachinalas' pervaya reakciya. Otmetim, chto v otlichii ot

-cikla zdes' slaboe vzaimodeistvie idet ne na letu, t.e. slaboe vzaimodeistvie i podbar'ernyi perehod razdeleny. Poskol'ku v CNO-cikle uchastvuyut yadra s bolee vysokim zaryadami, on idet pri bolee vysokoi temperature, prichem zavisimost' ot temperatury bolee krutaya, chem v

-cikle. Energovydelenie vo vsem CNO-cikle v raschete na odnu reakciyu ${}^{14}{\mathrm{N}}+p$ (samuyu medlennuyu) ravno 24,97 MeV. Vypishem polnuyu skorost' energovydeleniya v CNO-cikle:

$\displaystyle \varepsilon=\varepsilon_0\rho X_{\rm H}X_{\rm CNO}(T/T_0)^n\;[$ erg/g c $\displaystyle ]$

	$\varepsilon_0$
6	$9\cdot10^{-10}$	27,3
10	$3,4\cdot10{-4}$	22,9
15	1,94	19,9
20	$4,5\cdot10^2$	18,0
30	$4,1\cdot10^5$	15,6
50	$6,2\cdot10^8$	13,6
100	$1,9\cdot10{12}$	10,2

Z a d a ch i.

1. Podschitat', pri kakoi temperature D vygoraet za let. To zhe dlya ${}^{3}{\mathrm{He}}$ .

2. Naiti usloviya, pri kotoryh energovydelenie

$\displaystyle \varepsilon_{\rm CNO}=\varepsilon_{pp}.$

3. Vychislit' skorost' reakcii:
a). $\displaystyle{{}^{3}{\mathrm{He}}+p= {}^{4}{\mathrm{He}}+e^++\nu}$
(v etoi reakcii vydelyayutsya vysokoenergichnye neitrino),
b). $\displaystyle{{}^{3}{\mathrm{He}}+e^-\to {}^{}{\mathrm{T}}+\nu}$
(ukazanie: ispol'zovat' eksperimental'nye dannye po raspadu $\mathrm{T}\to{}^{3}{\mathrm{He}}+e^-+\widetilde\nu$ : energiya (ne vklyuchaya ) 0,0186 MeV, vremya zhizni 12,26 let. Rassmotret' ravnovesie s nevyrozhdennymi elektronami pri vysokoi temperature),
v). $\displaystyle{\mathrm{T}+p\to {}^{4}{\mathrm{He}}+\gamma\,}$

<< 5.4 Slaboe vzaimodeistvie | Oglavlenie | 5.6 Poiski solnechnyh neitrino >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce