<< 5.6 Poiski solnechnyh neitrino | Oglavlenie | 6.2 Sootnoshenie massa-svetimost' >>
6. Stroenie i ustoichivost' zvezd
Subsections
- 6.1 Uravneniya zvezdoi struktury
- 6.2 Sootnoshenie massa-svetimost'
- 6.3 Teplovaya ustoichivost' zvezd
- 6.4 Evolyuciya zvezd glavnoi posledovatel'nosti
- 6.5 Gorenie geliya: 3
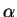 -reakciya
-reakciya
- 6.6 Opredelenie vozrasta skoplenii
- 6.7 Kachestvennaya kartina evolyucii zvezdy
6.1 Uravneniya zvezdoi struktury
V samoi obshei postanovke raschet vnutrennego stroeniya zvezd svoditsya k integrirovaniyu chetyreh differencial'nyh uravnenii, kazhdoe iz kotoryh my podrobno rassmatrivali v predydushih glavah. Vypishem seichas ih vmeste.
1. Uravnenie massy:
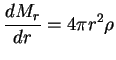 ili
ili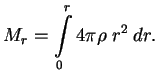
2. Uravnenie gidrostaticheskogo ravnovesiya:
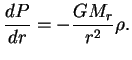
3. Uravnenie perenosa energii v diffuzionnom priblizhenii:
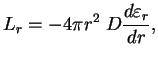
Perepishem eto uravnenie v vide
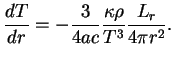
4. Uravnenie energeticheskogo balansa:
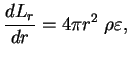
Eti differencial'nye uravneniya sleduet dopolnit' uravneniem sostoyaniya
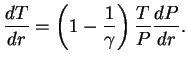
Tol'ko chto obosobivshuyusya v rezul'tate kondensacii mezhzvezdnogo gaza zvezdu razumno
schitat' himicheski odnorodnoi. Kak pokazyvayut raschet, evolyuciya zvezdy idet razlichnymi
putyami v zavisimosti ot togo, ostaetsya li zvezda himicheski odnorodnoi ili zhe
izmeneniya himicheskogo sostava proishodyat tol'ko tam, gde protekayut yadernye
reakcii, t. e. v ee central'nyh oblastyah. U malomassivnyh zvezd(
![]() )
konvekciei mozhet byt' ohvachena bol'shaya chast' zvezdy, poetomu zdes' peremeshivanie
privodit k tomu, chto himicheskii sostav menyaetsya u vsei zvezdy v celom. U bolee
massivnyh zvezd konvekciya otsutstvuet voobshe libo proishodit v nebol'shoi
central'noi chasti, gde vydelyaetsya energiya, i dlya nih izmenenie himicheskogo sostava
yavlyaetsya funkciei tol'ko lagranzhevoi koordinaty i proporcional'no skorosti vydeleniya
yadernoi energii:
)
konvekciei mozhet byt' ohvachena bol'shaya chast' zvezdy, poetomu zdes' peremeshivanie
privodit k tomu, chto himicheskii sostav menyaetsya u vsei zvezdy v celom. U bolee
massivnyh zvezd konvekciya otsutstvuet voobshe libo proishodit v nebol'shoi
central'noi chasti, gde vydelyaetsya energiya, i dlya nih izmenenie himicheskogo sostava
yavlyaetsya funkciei tol'ko lagranzhevoi koordinaty i proporcional'no skorosti vydeleniya
yadernoi energii:
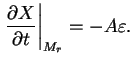
V dal'neishem budem rassmatrivat' modeli bez konvekcii. Itak, imeem chetyre differencial'nyh
uravneniya dlya velichin
![]() i
i ![]() s granichnymi usloviyami:
s granichnymi usloviyami:
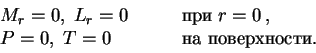
V centre mozhno var'irovat' dva parametra ![]() i
i ![]() .
.
Esli teper' my budem integrirovat' eti uravneniyami s fiksirovannymi nachal'nymi
parametrami, to ne vsegda ![]() i
i ![]() obratyatsya v nul' odnovremenno na poverhnosti
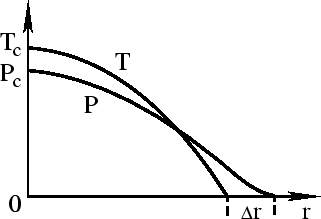
(ris. 31). Eto uslovie (
obratyatsya v nul' odnovremenno na poverhnosti
(ris. 31). Eto uslovie (
![]() ) nakladyvaet dopolnitel'noe ogranichenie na
) nakladyvaet dopolnitel'noe ogranichenie na
![]() i
i ![]() . Poetomu semeistvo reshenii budet odnoparametricheskim (po
. Poetomu semeistvo reshenii budet odnoparametricheskim (po ![]() ili
ili
![]() ). Pri dannom
). Pri dannom ![]() est' odno
est' odno ![]() , takoe chto
, takoe chto
![]() . Itak, pri
uchete etogo usloviya
. Itak, pri
uchete etogo usloviya
![]() . Esli by my rassmatrivali tol'ko
mehanicheskoe ravnovesie, to mozhno bylo by var'irovat' dva parametra (skazhem
. Esli by my rassmatrivali tol'ko
mehanicheskoe ravnovesie, to mozhno bylo by var'irovat' dva parametra (skazhem ![]() i
i
![]() ). No eshe neobhodimo, chtoby vydelenie energii i ee otvod kompensirovali drug
druga (uslovie teplovogo balansa). Eto dopolnitel'noe uslovie ogranichivaet
kolichestvo reshenii: dlya dannogo
). No eshe neobhodimo, chtoby vydelenie energii i ee otvod kompensirovali drug
druga (uslovie teplovogo balansa). Eto dopolnitel'noe uslovie ogranichivaet
kolichestvo reshenii: dlya dannogo ![]() est' edinstvennaya model' s odnim znacheniem
massy, sledovatel'no, dlya dannoi massy est' opredelennoe znachenie
est' edinstvennaya model' s odnim znacheniem
massy, sledovatel'no, dlya dannoi massy est' opredelennoe znachenie ![]() i opredelennaya
svetimost'6.1.
i opredelennaya
svetimost'6.1.
<< 5.6 Poiski solnechnyh neitrino | Oglavlenie | 6.2 Sootnoshenie massa-svetimost' >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |