Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Fizicheskie osnovy stroeniya i evolyucii zvezd
<< 6.6 Opredelenie vozrasta skoplenii | Oglavlenie | 7. Novye fizicheskie faktory... >>

6.7 Kachestvennaya kartina evolyucii zvezdy

Evolyuciya zvezd s massoi bol'she i men'she 2,5$ \,M_\odot$ idet po-raznomu. Pri $ M>2,5\,M_\odot$ v izotermicheskom gelievom yadre rastet temperatura i v dal'neishem vozmozhno zazhiganie i spokoinoe gorenie geliya. Dlya zvezd s men'shei massoi v izotermichesom yadre nastupaet vyrozhdenie, pri kotorom sila tyazhesti uravnoveshivaetsya davleniem vyrozhdennyh elektronov. Esli v takom yadre nachnutsya yadernye reakcii, to pri ego dostatochno bol'shoi masse mozhet proizoiti termoyadernyi vzryv, tak kak povyshenie temperatury pochti ne budet soprovozhdat'sya odnovremennym povysheniem davleniya. Pri massah $ 4\,M_{\odot}<M<8\,M_{\odot}$ nastupaet vyrozhdenie ugleroda v centre. Vozmozhny usloviya, kogda uglerodnoe yadro zvezdy sgoraet pochti mgnovenno i mozhet byt' dostignuta svetimost' $ \sim$ $ 10^{10}\;L_{\odot}$. Takoi vzryv mozhet byt' otozhdestvlen so vspyshkoi sverhnovoi.

V etom razdele my hotim na prostyh formulah (hotya i priblizhennyh) pokazat', kak v rezul'tate evolyucii, iz-za vyrozhdeniya v centre, teploemkost' zvezdy mozhet stat' polozhitel'noi, i voznikaet teplovaya neustoichivost'.

Vsya sut' v tom, chto my rassmatrivaem evolyuciyu zvezdy s dannoi massoi, prichem $ P$ i $ \rho $ svyazany mezhdu soboi usloviyami gidrostaticheskogo ravnovesiya. Evolyuciya postepenno menyaet svyaz' mezhdu $ P$ i $ \rho $. Pri etom nel'zya zabyvat', chto zvezda yavlyaetsya protyazhennoi, neodnorodnoi sistemoi, poetomu neobhodimo govorit' libo o srednih znacheniyah $ <\!\!P\!>$ i $ <\!\!\rho\!>$, libo o znacheniyah v centre $ P_c$ i $ \rho_c$. Nizhe dlya opredelennosti budem rassmatrivat' $ P_c$ i $ \rho_c$.

Strukturu zvezdy mozhno priblizhenno opisat' politropoi. Pust' indeks politropy $ n=3$. Togda

$\displaystyle P(r)=P_c (\rho/\rho_c)^{4/3}, $

$\displaystyle <\!\!\rho\!>={1\over {54}}\;\rho_c,\qquad P_c=\underbrace{P_1\;GM^{2/3}}_a\;\rho_c^{4/3}. $

Nizhe indeks $ c$ budem opuskat'. Itak,

$\displaystyle P=a\rho^{4/3} $

gde $ a\sim M^{2/3}$.

Rassmotrim snachala predel'nyi sluchai vyrozhdennogo elektronnogo gaza s $ T=0$. Togda davlenie svyazano s plotnost'yu po formule

$\displaystyle P=$const$\displaystyle \cdot \rho\;\Bigl[\underbrace{\left((m_ec^2)^2+p_{\mbox{\sc f}}^2c^2 \right)^{1/2}}_{E_{\mbox{\sc f}}}-m_ec^2\Bigr], $

gde $ p_{\mbox{\sc f}}=m_ecx$, $ x=(\rho/\mu_e\cdot 10^6)^{1/3}$. (Eta formula ne tochnaya! No ona pravil'no peredaet asimptotiki uravneniya sostoyaniya vyrozhdennogo gaza.) Vidim, chto pri $ x=1$, $ p_{\mbox{\sc f}}=m_ec$, sledovatel'no, $ x=1$ otmechaet granicu relyativizma (sm. 2.4). Itak,

$\displaystyle P\sim\rho\;\left[\left((m_ec^2)^2+b\rho^{2/3}\right)^{1/2}-m_ec^2\right]\,. $

Uchtem teper' vklad davleniya teplovogo dvizheniya chastic, vvodya funkciyu $ f(T)$, takuyu chto

$\displaystyle P\sim \rho \,\left[\left((m_ec^2)^2+b\rho^{2/3}+f(T)\right)^{1/2}-m_ec^2\right]=a\rho^{4/3}.$ (6.2)

Zdes' $ f(T)$ -- rastushaya funkciya temperatury, prichem v nerelyativistskoi oblasti $ f\sim T$, a v ul'trarelyativistskoi $ \sim T^2$. Perepishem sootnoshenie (2) v vide

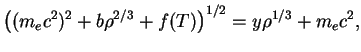
$\displaystyle \left((m_ec^2)^2+b\rho^{2/3}+f(T)\right)^{1/2}=y\rho^{1/3}+m_ec^2, $

gde $ y\sim a$ -- nekotoraya novaya konstanta, i vozvedem poslednee sootnoshenie v kvadrat. Togda $ (m_ec^2)^2$ sokratitsya, i my poluchim

$\displaystyle f(T)=2y\rho^{1/3}m_ec^2+(y^2-b)\rho^{2/3}. $

Pri $ \rho \to 0$ (nerelyativistskaya oblast') $ f(T)\sim T$ i otsyuda

$\displaystyle T\sim \rho^{1/3}M^{2/3}, $

poskol'ku $ y\sim a\sim M^{2/3}$. Itak, my poluchili odin iz variantov teoremy viriala.

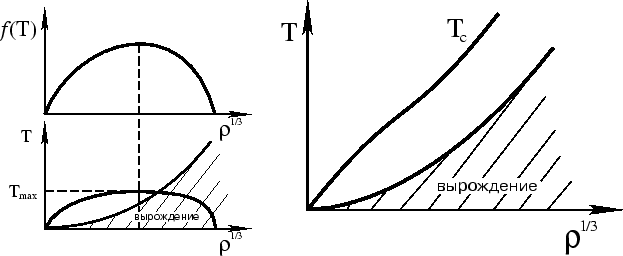
Pri bol'shih plotnostyah povedenie temperatury zavisit ot togo, polozhitel'na ili otricatel'na skobka $ (y^2-b)$ pri $ \rho^{2/3}$. Esli $ y^2<b$ (t. e. massa mala, $ y\sim M^{2/3}$ i skobka otricatel'na), to legko uvidet', chto sushestvuet ravnovesie pri $ T=0,\;\rho\neq 0$, i krome etogo est' maksimum temperatury (ris. 40). Legko naiti sootnoshenie mezhdu maksimal'noi plotnost'yu ($ T=0$) i plotnost'yu, sootvetstvuyushei maksimumu temperatury: $ \rho_{\mbox{\sc t}\,\max}\simeq \left.\frac{1}{8}\rho\right\vert _{T=0}$ (tak kak $ \rho^{1/3}_{\mbox{\sc t}\,\max}=\left.{1\over 2} \rho^{1/3}\right\vert _{T=0}$). Takim obrazom, my vidim, chto pri postepennom szhatii temperatura rastet, dostigaet maksimuma, a zatem ubyvaet. Naidem asimptotiku $ T_{\max}$ dlya malyh mass. Imeem

$\displaystyle \left.\rho\right\vert _{T=0}\sim (y/b)^3\sim M^2, $

otsyuda

$\displaystyle T_{\max}\sim\rho^{1/3}\sim M^{2/3}. $

Konkretnye raschety pokazyvayut, chto dlya mass, men'shih chem $ 0,08\div 0,10\,M_{\odot}$, maksimal'no vozmozhnaya temperatura nizhe znacheniya, pri kotorom nachinaet goret' vodorod. Etot predel slabo zavisit ot himicheskogo sostava zvezdy, tak kak on poluchaetsya iz obshih termodinamicheskih sootnoshenii. Mozhno takzhe naiti, chto dlya mass $ M<0,35\,M_{\odot}$ ne zagoraetsya gelii, t. e. ne idet $ 3\alpha$-reakciya $ 3\,{}^{4}{\mathrm{He}}\rightleftarrows\mathrm{C}$, a pri $ M<0,8\,M_{\odot}$ ne gorit uglerod (v reakcii $ {}^{12}{\mathrm{C}}+{}^{12}{\mathrm{C}}\rightleftarrows{}^{24}{\mathrm{Mg}}$). Nalichie maksimuma temperatury vazhno i v drugom otnoshenii. Imenno blagodarya zamedleniyu rosta temperatury v malomassivnyh zvezdah s rostom central'noi plotnosti zvezda popadaet v oblast' vyrozhdeniya (sm. ris. 40). Esli eto proishodit pri dostatochno vysokoi temperature, to vzryv neizbezhen.

Ris. 41.

Pri $ y^2<b\qquad(M<M_{Ch}=1,4\;M_{\odot})$ obrazuyutsya belye karliki. Massy nablyudaemyh belyh karlikov $ \sim$ $ 0,6\;M_{\odot}$. No zvezda s massoi $ \sim$ $ 0,6\;M_{\odot}$ zhivet na glavnoi posledovatel'nosti okolo $ 3\cdot10^{10}$ let, t.e. bol'she vozrasta Vselennoi. Eto eshe odin argument v pol'zu togo, chto nablyudaemye seichas belye karliki proizoshli iz bolee massivnyh zvezd, kotorye v processe evolyucii poteryali znachitel'nuyu chast' svoei massy. Krome togo, imeyutsya dvoinye zvezdnye sistemy, sostoyashie iz belogo karlika s massoi poryadka $ 0,6\,M_{\odot}$, i zvezdy glavnoi posledovatel'nosti s massoi poryadka $ 2\,M_{\odot}$. Takoe sochetanie ob'ektov vozmozhno tol'ko lish' v tom sluchae, esli na meste belogo karlika ranee byla bolee massivnaya zvezda, poteryavshaya na stadii krasnogo giganta bol'shuyu chast' svoei massy. Pochti vsya uteryannaya massa mozhet byt' zahvachena vtorym komponentom.

Teper' rassmotrim sluchai bol'shih mass $ (y^2>b,\;M>1,4\;M_{\odot}$ -- chandrasekarovskii predel). Dlya etih mass v ramkah nashih priblizhennyh raschetov net ogranichenii na rost plotnosti i temperatury (ris. 41). Zagoranie tyazhelyh elementov (C, O, Mg) nachinaetsya v nevyrozhdennyh usloviyah. No sleduet pomnit', chto my predpolagali postoyanstvo chisla elektronov, neizmennost' himicheskogo sostava, ne uchli effekty OTO. Na samom dele iz-za etih effektov pri dostizhenii nekotoroi kriticheskoi plotnosti nachnutsya katastroficheskie sobytiya.

Zadacha. Raschet kosmologicheskih modelei daet soderzhanie deiteriya otnositel'no vodoroda $ 10^{-3}$-$ 10^{-4}$. Naiti znachenie massy zvezdy, pri kotoroi poidet reakciya

$\displaystyle \rm {D}+p\to{}^{3}{\mathrm{He}}+\gamma, $

(t. e. nuzhno proverit' ne tol'ko, smozhet li nachat'sya reakciya, no i uspeet li ona proiti po sravneniyu so vremenem ostyvaniya, zaderzhit li ona ostyvanie).
<< 6.6 Opredelenie vozrasta skoplenii | Oglavlenie | 7. Novye fizicheskie faktory... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 3.0 [golosov: 120]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya