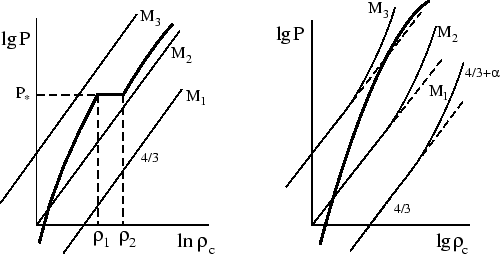<< 7.1 Obshaya teoriya otnositel'nosti | Oglavlenie | 7.3 Dva tipa energeticheskih ... >>
7.2 Neitronizaciya
Voz'mem oblast', gde ![]() i
i
![]() , t.e. temperatura nizka,
a plotnost' velika. Pri etom teplovye dvizheniya nerelyativistskie, a princip Pauli iz-za
vysokoi plotnosti zastavlyaet elektrony dvigat'sya s relyativistskimi skorostyami. S
tochki zreniya izlucheniya eto veshestvo holodnoe, tak kak nizhnie sostoyaniya zanyaty, no s
tochki zreniya yadernyh reakcii eto veshestvo goryachee, tak kak chasticy mogut ischezat'
i otdavat' svoyu energiyu v processah sleduyushego tipa:
, t.e. temperatura nizka,
a plotnost' velika. Pri etom teplovye dvizheniya nerelyativistskie, a princip Pauli iz-za
vysokoi plotnosti zastavlyaet elektrony dvigat'sya s relyativistskimi skorostyami. S
tochki zreniya izlucheniya eto veshestvo holodnoe, tak kak nizhnie sostoyaniya zanyaty, no s
tochki zreniya yadernyh reakcii eto veshestvo goryachee, tak kak chasticy mogut ischezat'
i otdavat' svoyu energiyu v processah sleduyushego tipa:
Takie processy nazyvayut neitronizaciei veshestva
(sm. razdel 5.4). Neitronizaciya -- porogovyi
process i dlya raznyh elementov proishodit pri raznyh energiyah elektronov. Naprimer, dlya
pervoi reakcii porog neitronizacii 18 keV, dlya vtoroi -- 20 MeV, dlya tret'ei -- 4
MeV. Tak kak granichnaya energiya Fermi odnoznachno svyazana s plotnost'yu, to sootvetstvenno
neitronizaciya veshestva dlya razlichnyh elementov nachinaetsya pri raznyh plotnostyah.
Naprimer, pervaya reakciya mozhet idti i pri
![]() g/sm
g/sm![]() , a vtoraya idet
tol'ko pri
, a vtoraya idet
tol'ko pri
![]() g/sm
g/sm![]() .
.
K chemu vedet neitronizaciya? My vidim, chto v etih reakciyah umen'shaetsya kolichestvo elektronov, sohranyaetsya chislo yader, no ih zaryad ubyvaet. Zdes' my imeem delo s ochen' tonkim ravnovesiem.
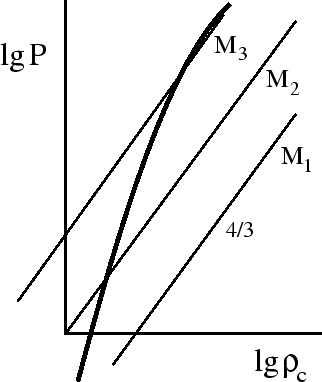
Na grafike ![]() -
-![]() krivaya uravneniya sostoyaniya veshestva v nerelyativistskoi
oblasti imeet naklon 5/3, a v relyativistskoi 4/3
(sm. ris. 42). Budem na etom zhe
grafike nanosit' pryamye
krivaya uravneniya sostoyaniya veshestva v nerelyativistskoi
oblasti imeet naklon 5/3, a v relyativistskoi 4/3
(sm. ris. 42). Budem na etom zhe
grafike nanosit' pryamye
![]() , kotorye poluchayutsya iz usloviya
gidrostaticheskogo ravnovesiya. Tochki ih peresecheniya s predydushei krivoi dadut polozheniya
ravnovesiya dlya razlichnyh mass. Ochevidno, v nachale tochka peresecheniya dvizhetsya medlenno s
uvelicheniem massy, a zatem -- ochen' bystro. V ideal'nom sluchae (t.e. bez ucheta effektov
OTO i neitronizacii)
, kotorye poluchayutsya iz usloviya
gidrostaticheskogo ravnovesiya. Tochki ih peresecheniya s predydushei krivoi dadut polozheniya
ravnovesiya dlya razlichnyh mass. Ochevidno, v nachale tochka peresecheniya dvizhetsya medlenno s
uvelicheniem massy, a zatem -- ochen' bystro. V ideal'nom sluchae (t.e. bez ucheta effektov
OTO i neitronizacii)
![]() pri
pri
![]() (chandrasekarovskii
predel).
(chandrasekarovskii
predel).
Iz-za neitronizacii na krivoi ![]() -
-![]() poyavlyayutsya izlomy, tak kak elektrony,
kotorye obespechivayut uprugost' veshestva, ``vdavlivayutsya'' v yadra.
poyavlyayutsya izlomy, tak kak elektrony,
kotorye obespechivayut uprugost' veshestva, ``vdavlivayutsya'' v yadra.
Neitronizaciya -- eto fazovyi perehod pervogo roda, pri kotorom davlenie zavisit ot plotnosti
tak, kak eto izobrazheno na ris. 43.
My vidim, chto esli ran'she ravnovesie massy ![]() eshe bylo
vozmozhno, to teper' eto ne tak, t.e. uzhe pri
eshe bylo
vozmozhno, to teper' eto ne tak, t.e. uzhe pri
![]() proishodit poterya ustoichivosti.
proishodit poterya ustoichivosti.
S drugoi storony, effekty OTO iz-za togo, chto davlenie imeet ``ves'', izmenyayut
usloviya gidrostaticheskogo ravnovesiya. Tak kak teper' sila tyazhesti proporcional'na
![]() , uslovie ravnovesiya teper' zapishetsya v vide
, uslovie ravnovesiya teper' zapishetsya v vide
![]() ,
gde
,
gde ![]() , t.e. naklon pryamyh
, t.e. naklon pryamyh ![]() ,
, ![]() ,
, ![]() narastaet s uvelicheniem
narastaet s uvelicheniem
![]() (ris. 44).
(ris. 44).
Chandrasekar ogranichil znachenie massy ![]() , a
, a ![]() moglo byt' beskonechnym. Teper'
my vidim, chto est' i predel'noe znachenie
moglo byt' beskonechnym. Teper'
my vidim, chto est' i predel'noe znachenie ![]() .
.
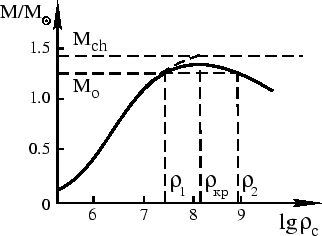
Vse eti effekty privodyat k izgibam krivoi ![]() , chto v konechnom itoge privodit
k potere ustoichivosti (ris. 45).
Formal'nyi raschet s raznymi znacheniyami
, chto v konechnom itoge privodit
k potere ustoichivosti (ris. 45).
Formal'nyi raschet s raznymi znacheniyami ![]() daet maksimal'noe znachenie massy
daet maksimal'noe znachenie massy ![]() i pri
i pri
![]() dva resheniya s razlichnymi
znacheniyami
dva resheniya s razlichnymi
znacheniyami ![]() . Reshenie s bol'shei plotnost'yu
(
. Reshenie s bol'shei plotnost'yu
(
![]() na
ris. 45)
okazyvaetsya neustoichivym. Kak eto mozhno pokazat'?
na
ris. 45)
okazyvaetsya neustoichivym. Kak eto mozhno pokazat'?
My vidim, chto dlya odnoi massy ![]() sushestvuet dva resheniya. Mozhno schitat', chto
odno iz etih reshenii (skazhem s
sushestvuet dva resheniya. Mozhno schitat', chto
odno iz etih reshenii (skazhem s
![]() ) yavlyaetsya vozmusheniem drugogo
(
) yavlyaetsya vozmusheniem drugogo
(
![]() ). Eto znachit,chto
). Eto znachit,chto
V nashem sluchae ![]() ot
ot ![]() ne zavisit, t.e.
ne zavisit, t.e. ![]() v obshem reshenii.
Poskol'ku my znaem, chto pri
v obshem reshenii.
Poskol'ku my znaem, chto pri
![]() modeli byli ustoichivymi, dlya nih
bylo
modeli byli ustoichivymi, dlya nih
bylo
![]() . Pri
. Pri
![]() my poluchili, chto
my poluchili, chto
![]() dlya
nekotorogo
dlya
nekotorogo ![]() . Dlya fizika etogo uzhe dostatochno, chtoby utverzhdat', chto pri
. Dlya fizika etogo uzhe dostatochno, chtoby utverzhdat', chto pri
![]() , t.e.
, t.e.
![]() , a eto i oznachaet
neustoichivost'. Konechno, mozhno ubedit'sya v etom i bolee strogo, naprimer, esli
issledovat' formu ekstremuma energii. Pri
, a eto i oznachaet
neustoichivost'. Konechno, mozhno ubedit'sya v etom i bolee strogo, naprimer, esli
issledovat' formu ekstremuma energii. Pri
![]() ekstremum, sootvetstvuyushii
ravnovesiyu, yavlyaetsya minimumom, a pri
ekstremum, sootvetstvuyushii
ravnovesiyu, yavlyaetsya minimumom, a pri
![]() -- maksimumom.
-- maksimumom.
Pri ostyvanii zvezdy s
![]() pri nekotoroi temperature proishodit sryv. Do
etogo momenta evolyuciya opredelyaetsya skorost'yu ostyvaniya, zatem proishodit poterya
ustoichivosti s harakternym gidrodinamicheskim vremenem.
pri nekotoroi temperature proishodit sryv. Do
etogo momenta evolyuciya opredelyaetsya skorost'yu ostyvaniya, zatem proishodit poterya
ustoichivosti s harakternym gidrodinamicheskim vremenem.
<< 7.1 Obshaya teoriya otnositel'nosti | Oglavlenie | 7.3 Dva tipa energeticheskih ... >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |