Astronet > 7.3 Dva tipa energeticheskih poter'

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 7.2 Neitronizaciya | Oglavlenie | 7.4 Rol' neitrino v ... >>

7.3 Dva tipa energeticheskih poter'

Obychnaya zvezda nahoditsya v gidrostaticheskom ravnovesii, pri kotorom sily tyagoteniya uravnovesheny gradientom davleniya. Esli net vyrozhdeniya, to davlenie teplovoe. Poteri energii zvezdoi privodyat k tomu, chto sostoyanie ravnovesiya vse vremya izmenyaetsya. Pri etom nado razlichat' dva principial'no raznyh tipa energeticheskih poter' -- obratimye i neobratimye.

1. Processy, pri kotoryh proishodyat odnokratnye poteri energii, t.e. processy tipa ionizacii, dissociacii, rozhdenie par $e^+,\;e^-$ i t.p. yavlyayutsya obratimymi. Posle togo kak proizoshlo prevrashenie, poteri energii prekrashayutsya. Takie processy mozhno harakterizovat' velichinoi $E\;[$ erg/g, t.e. kolichestvom energii, kotoruyu nuzhno zatratit', chtoby perevesti veshestvo v novoe sostoyanie.

2. Processy, pri kotoryh obrazuyutsya chasticy, sposobnye uhodit' iz sistemy i unosit' energiyu, yavlyayutsya neobratimymi. Tipichnymi primerami yavlyaetsya rozhdenie par $\gamma$ -kvantov i osobenno par neitrino-antineitrino. Zvezdy pochti vsegda prakticheski prozrachny dlya neitrino. Na konechnyh stadiyah evolyucii poteri energii cherez neitrinnye processy yavlyayutsya preobladayushimi. Processy takogo tipa harakterizuyutsya velichinoi $Q\;[$ erg/g $\cdot$ s, t.e. energiei, teryaemoi grammom veshestva v sekundu.

Rassmotrim bolee podrobno obratimye poteri. Etot tip poter' luchshe nazvat' ne poteryami , a osobennostyami uravneniya sostoyaniya. Rassmotrim uravnenie sostoyaniya $P(\rho, S)$ , gde -- udel'naya entropiya dlya ideal'nogo gaza, sostoyashego iz atomarnogo vodoroda.

Pri nizkoi temperature ( $T<T_{\mbox{ioniz}}$ )

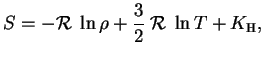
$\displaystyle S=-{\cal R}\;\ln\rho+\frac{3}{2}\;{\cal R}\;\ln T+K_{\rm H},$

${\cal R}$ -- universal'naya gazovaya postoyannaya, a $K_{\rm H}$ -- tak nazyvaemaya himicheskaya konstanta vodoroda.

Pri vysokoi temperature, kogda ves' vodorod ionizovan, gaz sostoit iz dvuh komponent -- protonnoi i elektronnoi. Poskol'ku entropiya additivna, poluchaem

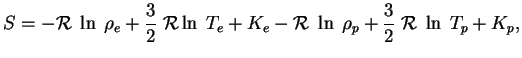
$\displaystyle S=-{\cal R}\;\ln\;\rho_e+{3\over 2}\;{\cal R}\ln\;T_e+K_e-{\cal R}\;\ln\;\rho_p+{3\over2} \;{\cal R}\;\ln\;T_p+K_{p},$

gde

-- himicheskie konstanty elektronnogo i protonnogo gazov. Tak kak staticheskie i atomnye vesa H i

pochti ravny, imeem $K_p\simeq K_H$ .

Iz pervogo sootnosheniya my vidim, chto

$\displaystyle T=e^{-2K_H/3{\cal R}}\;e^{2S/3{\cal R}}\;\rho^{2/3}.$

Takim obrazom, pri postoyannoi entropii $T\sim \rho^{2/3}$ , a davlenie

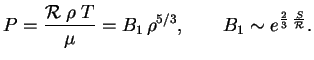$\displaystyle P={{\cal R}\;\rho\;T\over{\mu}}=B_1\,\rho^{5/3},\qquad B_1\sim e^{{2\over3}\;{S\over {\cal R}}}.$

(7.1)

S drugoi storony, pri $T\gg T_{\mbox{ioniz}}$

$\displaystyle P=B_2\rho^{5/3},\qquad B_2\sim e^{{1\over3}\;{S\over{\cal{R}}}},$

t.e. est' i do i posle ionizacii naklon pryamoi v peremennyh $\lg P\;$ - $\;\lg\rho$ odin i tot zhe i raven 5/3. No v promezhutochnoi oblasti my imeem pochti izotermicheskii uchastok, gde $P\sim\rho$ (ris. 46). Ionizaciya proishodit v uzkom intervale temperatur , poskol'ku po Saha

$\displaystyle [p][e^-]/[\mathrm{H}]\sim e^{-J/kT},$

gde

-- potencial ionizacii.


Ris. 46.	Ris. 47.

Po drugomu eto mozhno ponyat', esli vspomnit', chto v neionizovannom gaze $C_V\,dT=-P\,dV$ , , otkuda

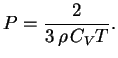
$\displaystyle P={2\over3\,\rho\, C_V T}.$

Posle ionizacii

. Iz-za togo, chto chast' raboty uhodit na ionizaciyu, davlenie okazyvaetsya nizhe, chem po formule (7.1).

Teper' zaimemsya figurami ravnovesiya. Rassmotrim vodorodnuyu samogravitiruyushuyu konfiguraciyu, kogda ionizaciya eshe ne proizoshla (model' protozvezdy). Yasno, chto pri etom proishodit szhatie, i na grafike $\lg P\;$ - $\;\lg\rho$ poyavlyayutsya tri ravnovesnyh resheniya, dva iz kotoryh ustoichivy, a odno neustoichivo (sm. ris. 47) ^7.1. Pri eshe bolee nizkih entropiyah ( men'shih ) ostaetsya odno ustoichivo sostoyanie. Yasno, chto perehod iz odnogo ustoichivogo sostoyaniya v drugoe proishodit skachkom.

Vse eto proishodit pri temperaturah $\sim 10^4$ K $\sim 1$ eV, t.e. pri temperaturah, gorazdo men'shih potenciala ionizacii ( $J\sim 13,6$ eV). V formule Saha eksponenta mala, no velik predeksponencial'nyi mnozhitel'.

Teper' rassmotrim drugoi mehanizm poteri ustoichivosti, kotoryi vazhen pri temperaturah $\sim$ 0,5 MeV. Eto mehanizm fotodissociacii zheleza, vpervye rassmotrennyi Hoilom i Faulerom:

$\displaystyle \gamma + {}^{56}{\mathrm{Fe}}\to {}^{52}{\mathrm{Cr}}+\alpha.$

Esli uzh nachalas' dissociaciya zheleza, to razvalivayutsya i drugie elementy, vplot' do geliya. Na chasticu pri etom pogloshaetsya energiya $\sim$ 7MeV. Vsego poluchaetsya 17 chastic (13 ${}^{4}{\mathrm{He}}+4n$ ). Takim obrazom polnaya energiya dissociacii sostavlyaet $J=17\times 7=120$ MeV na yadro ${}^{56}{\mathrm{Fe}}$ . Odnako fotodissociaciya nachinaetsya pri temperaturah $kT\ll J$ opyat' zhe iz-za bol'shoi velichiny predeksponencial'nogo mnozhitelya v formule Saha. Etot mnozhitel', kotoryi opisyvaet statisticheskii ves dissociirovannogo sostoyaniya, velik, tak kak obrazuetsya mnogo chastic.

V kachestve primera privedem dva znacheniya $T_{\mbox{dis}}$ pri raznyh plotnostyah:

$\rho\;($ g/sm
$T_{\mbox{dis}}\;$ (K)	$4,1\cdot10^9$	$5,8\cdot10^9$
$T_{\mbox{dis}}\;$ (MeV)	0,35	0,50

V rezul'tate fotodissociacii zheleza proishodit poterya ustoichivosti i zvezda nachinaet bystro (za gidrodinamicheskoe vremya) szhimat'sya. Etot process podoben vzryvu, no dvizhenie veshestva napravleno vnutr', poetomu on nazyvaetsya imploziei (v otlichie ot obychnogo vzryva ``explosion''). Krivye na ploskosti $\lg P\;$ - $\;\lg\rho$ pri etom podobny izobrazhennym na ris. 47.

Poskol'ku vo vneshnih sloyah zvezdy mogut ostavat'sya nesgorevshie elementy (C, O i pr.), a pri implozii proishodit sil'nyi nagrev veshestva, to vozmozhno vydelenie yadernoi energii, pri kotorom imploziya smenyaetsya obychnym vzryvom, napravlennym naruzhu. Ran'she dumali, chto etot mehanizm mozhet ob'yasnit' vzryv zvezd s massoi $M>10\;M_\odot$ kak sverhnovyh, odnako samye poslednie raschety pokazyvayut, chto imploziya ne smenyaetsya vzryvom. Energiya uhodit iz zvezdy v vide neitrino (sm. razdel 7.4).

V zaklyuchenie rassmotrim sluchai, kogda v termodinamicheskom ravnovesii mozhet nahodit'sya bol'shoe kolichestvo elektronno-pozitronnyh par. Pust' davlenie izlucheniya $\sim$ mnogo bol'she davleniya veshestva ${\cal R}\rho T$ , no plotnost' veshestva vse eshe bol'she plotnosti izlucheniya:

$\displaystyle \rho>aT^4/c^2.$

Iz termodinamicheskogo sootnosheniya

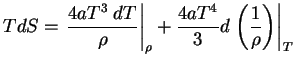
$\displaystyle TdS=\left.{4aT^3\;dT\over {\rho}}\right\vert _{\rho}+{4aT^4\over 3}d\left.\left( {1\over{\rho}}\right)\right\vert _T$

naidem udel'nuyu entropiyu

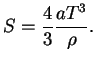
$\displaystyle S={4\over3}{aT^3\over{\rho}}.$

Itak,

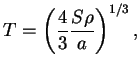
$\displaystyle T=\left({4\over3}{S\rho\over a}\right)^{1/3},$

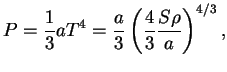
$\displaystyle P={1\over3}aT^4={a\over3}\left({4\over3}{S\rho\over a}\right)^{4/3},$

t.e. dlya chistogo izlucheniya pri postoyannoi entropii $P\sim \rho^{4/3}$ .

Ris. 48.

Pri temperaturah nachinaetsya intensivnoe rozhdenie par (). V predel'nom sluchae $kT\gg m_ec^2$ krome izlucheniya imeetsya ravnovesnyi relyativistskii elektronno-pozitronnyi gaz. Polnaya plotnost' energii pri etom

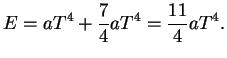
$\displaystyle E=aT^4+{7\over4}aT^4={11\over4}aT^4.$

Davlenie

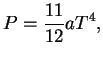
$\displaystyle P={11\over{12}}aT^4,$

i entropiya

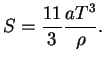
$\displaystyle S={11\over3}{aT^3\over{\rho}}.$

Takim obrazom, pri $kT\gg m_ec^2$ snova $P\sim \rho^{4/3}$ , no v promezhutochnom sluchae naklon krivoi na grafike $\lg P\;$ - $\;\lg\rho$ dolzhen byt' men'she 4/3 (sm. ris. 48). Pri otnositel'no nebol'shih plotnostyah, kogda davlenie opredelyalos' fotonnym gazom, zvezda uzhe byla na granice ustoichivosti ( $P\sim \rho^{4/3}$ ). Poetomu pri podhode k oblasti rozhdeniya elektron-pozitronnyh par uzhe net sostoyaniya ravnovesiya. Poetomu net sverhmassivnyh zvezd.

<< 7.2 Neitronizaciya | Oglavlenie | 7.4 Rol' neitrino v ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce