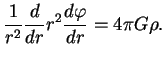Astronet > 1.2 Vektornoe pole uskorenii, teorema Gaussa, gravitacionnyi potencial, uravnenie Puassona

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 1.1 Energiya vzaimodeistviya ... | Oglavlenie | 1.3 Sfericheski-simmetrichnye polya tyag... >>

1.2 Vektornoe pole uskorenii, teorema Gaussa, gravitacionnyi potencial, uravnenie Puassona

Vvedem ponyatie vektornogo polya uskorenii $\vec a$ , sozdavaemyh gravitiruyushimi telami. Odna tochechnaya massa sozdaet pole uskorenii :

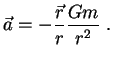
$\displaystyle \vec a=-{\vec r \over r}{Gm \over r^2} \; .$

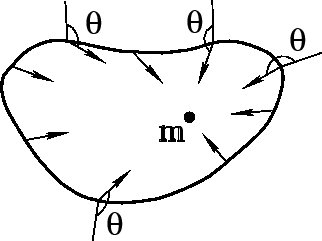
Okruzhim massu proizvol'noi zamknutoi poverhnost'yu (ris.1) i vychislim potok polya $\vec a$ cherez poverhnost' :

$\displaystyle \int\limits_S \vec a\;$

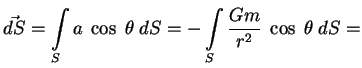$\displaystyle \vec {dS} =\int\limits_S a \;\cos\;\theta\;dS=-\int\limits_S {Gm \over r^2}\;\cos\;\theta\;dS= \cr$

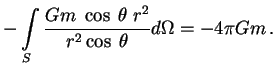$\displaystyle -\int\limits_S {Gm \; \cos\;\theta\;r^2 \over r^2\cos\;\theta}d \Omega=-4 \pi Gm\,. \cr$

Zdes' $\theta$ -- ugol mezhdu $\vec a$ i normal'yu k poverhnosti

. Vazhno otmetit', chto polnyi potok okazalsya nezavisyashim ot formy poverhnosti.

Esli imeetsya neskol'ko mass $m_1,\; m_2, \;m_3,\; ...\,,$ to pole $\vec a$ yavlyaetsya superpoziciei polei $\vec a_1,\;\vec a_2,\; ...,$ sozdavaemyh etimi massami

$\displaystyle \vec a=\vec a_1+\vec a_2+\vec a_3+\; \ldots$

$\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f01.ai}} \end{wrapfigure}$

Ris. 1.

Ispol'zuya eto svoistvo gravitacionnogo polya i okruzhaya poverhnost'yu neskol'ko mass, legko poluchit'

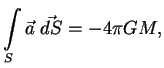
$\displaystyle \int\limits_S \vec a\; \vec {dS} =-4 \pi GM,$

gde $M=m_1+m_2+m_3+...\;.$

Mozhno ubedit'sya, chto massa, raspolozhennaya vne zamknutoi poverhnosti , ne daet vklada v $\int\limits_S \vec a\; \vec {dS}$ .

Takim obrazom, polnyi potok vektornogo polya $\vec a$ raven

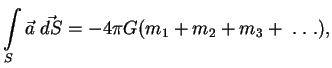
$\displaystyle \int\limits_S \vec a\; \vec {dS}=-4 \pi G(m_1+m_2+m_3+\;.\;.\;.),$

prichem v summu vhodyat tol'ko te massy, kotorye lezhat vnutri

. Eto polozhenie nazyvaetsya teoremoi Gaussa.

Primenim teoremu Gaussa k sfericheskomu sloyu. Pust' -- sfera radiusa , lezhashaya vnutri etogo sloya. Togda $4 \pi r^2\cdot a=0$ , t.k. vnutri net mass. Sledovatel'no, vnutri sfericheskogo sloya^1.1 $\; a=0$ . Okruzhim teper' sfericheski-simmetrichnuyu konfiguraciyu massy poverhnost'yu . Togda $a \cdot 4 \pi r^2=-4 \pi GM$ i . Itak, sfericheski-simmetrichnaya konfiguraciya sozdaet pole, ekvivalentnoe polyu tochechnoi massy, sosredotochennoi v ee centre.

Dlya malogo ob'ema mozhno napisat'

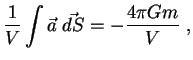
$\displaystyle {1 \over V} \int \vec a\; \vec {dS}=-{4 \pi Gm \over V} \; ,$

gde integral beretsya po poverhnosti ob'ema

, a

-- massa, zaklyuchennaya v etom ob'eme. V predele pri $V\to0$ otnoshenie

est' lokal'naya plotnost' $\rho$ , tak chto poluchim

$\displaystyle \mathop{\rm div}\; \vec a =-4 \pi G \, \rho.$

Cdelaem sleduyushii shag -- vvedem potencial gravitacionnogo polya soglasno usloviyu:

$\displaystyle \vec a=-\mathop{\rm grad}\, \varphi.$

Eto vsegda mozhno sdelat', tak kak gravitacionnoe pole konservativno: vsegda $\oint \vec a\; \vec {dl}$ =0, t.e. $\mathop{\rm rot}\vec a =0$ , a eto i oznachaet vozmozhnost' vvedeniya potenciala. Teper' imeem

$\displaystyle \mathop{\rm div}\, \vec a =-\mathop{\rm div}\,\mathop{\rm grad}\, \varphi=- \Delta \varphi=-4 \pi G \, \rho,$

ili

$\displaystyle \Delta \varphi=4 \pi G \; \rho.$

My poluchili uravnenie Puassona -- osnovnoe uravnenie teorii potenciala. Differencial'nyi operator $\mathop{\rm div}\mathop{\rm grad}\equiv \Delta$ nazyvayut laplasianom. V dekartovyh koordinatah

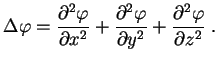
$\displaystyle \Delta \varphi= {\partial^2 \varphi \over \partial x^2}+ {\partial^2 \varphi \over \partial y^2}+{\partial^2 \varphi \over \partial z^2} \; .$

V sfericheskih koordinatah ( $r, \; \theta ,\; \alpha$ )

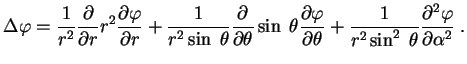
$\displaystyle \Delta \varphi={1 \over r^2}{\partial \over \partial r}r^2{\parti... ...1 \over r^2 \sin^2 \;\theta} {\partial^2 \varphi \over \partial \alpha ^2} \;.$

Netrudno ponyat', otkuda beretsya takoi vid dlya $\Delta$ . Rassmotrim chlen ${1 \over r^2} {\partial \over \partial r}r^2{\partial\varphi\over\partial r}$ , kotoryi ostaetsya v uravnenii Puassona dlya sfericheski-simmetrichnoi zadachi. Ochevidno, chto $4 \pi r^2 \partial\varphi\over\partial r$ -- eto potok polya uskorenii $\vec a={\partial\varphi \over\partial r}$ cherez sferu radiusa

. Raznost' potokov $\vec a$ cherez sfery

i $r+ \delta r$ ravna $4 \pi\delta r {\partial \over \partial r}r^2{\partial \varphi\over\partial r}$ , ob'em mezhdu sferami -- $4 \pi r^2\delta r$ . Razdeliv raznost' potokov $\vec a$ na ob'em, poluchaem $\Delta \varphi={1 \over r^2} {\partial \over \partial r}r^2{\partial\varphi\over\partial r}$ . Yasno, chto v zadache s cilindricheskoi simmetriei iz teh zhe soobrazhenii poluchim $\Delta \varphi={1 \over r}{\partial \over \partial r}r{\partial\varphi\over\partial r}$ (

-- cilindricheskii radius).

Itak, dlya sfericheski-simmetrichnogo raspredeleniya plotnosti

$\displaystyle {1\over r^2}{d\over dr}r^2 {d\varphi \over dr}=4 \pi G \rho.$

(1.1)

<< 1.1 Energiya vzaimodeistviya ... | Oglavlenie | 1.3 Sfericheski-simmetrichnye polya tyag... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce