Astronet > 7.4 Rol' neitrino v evolyucii zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 7.3 Dva tipa energeticheskih ... | Oglavlenie | 8. Vvedenie v OTO >>

7.4 Rol' neitrino v evolyucii zvezd

Vyshe my uzhe otmechali kachestvennoe otlichie processov s rozhdeniem neitrino ot drugih mehanizmov poter' energii. Rozhdayas' neitrino prakticheski besprepyatstvenno uhodyat iz zvezdy i navsegda unosyat s soboi energiyu. Kak i ostal'nye processy (dissociaciya yader, rozhdenie par i pr.), neitrinnye processy soprovozhdayutsya zatratoi energii i ponizheniem davleniya. Odnako esli ran'she my imeli tol'ko izmenenie sostoyanie ravnovesiya iz-za rozhdeniya novyh chastic, to teper' vsledstvie energeticheskih poter' polnogo ravnovesnogo sostoyaniya voobshe net: $\partial S/\partial t\neq 0$ ( -- entropiya). Entropiya inogda padaet! V etom net protivorechiya: padaet entropiya veshestva v centre yadra, no voznikaet entropiya neitrino, uletevshih ot zvezdy.

No nepolnoe ravnovesie tozhe mozhno izluchat'. Naprimer, gremuchii gaz: $\rm {H}_2+ \rm {O}_2$ -- my mozhem rassmatrivat' ego rasshirenie, szhatie i prochee, prichem vse eti processy budut ravnovesnymi, krome odnogo -- processa sgoraniya. To zhe mozhno skazat' i o lyuboi smesi veshestv (naprimer, $\rm {H}+\rm {He}$ , esli imet' v vidu yadernye reakcii), tak kak polnoe ravnovesie -- eto yadra zheleza.

V sostoyanii polnogo termodinamicheskogo ravnovesiya koncentraciya neitrino proporcional'na . Plotnost' energii i davlenie $\sim$ . Odnako v zvezdah neitrino rozhdayutsya i uhodyat, poetomu ih istinnaya koncentraciya gorazdo men'she ravnovesnoi.

Pri rassmotrenii goreniya vodoroda my uzhe uchityvali rozhdenie neitrino. No togda uchet neitrino svodilsya prosto k effektivnomu umen'sheniyu kaloriinosti yadernogo topliva. Naprimer, esli skorost' reakcii

$\displaystyle 4\rm {H}\to^4\rm {He}$ ravna $\displaystyle ~q~[$ aktov/g $\displaystyle \cdot$ s $\displaystyle ],$

to nagrev

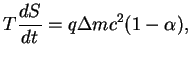
$\displaystyle T{dS\over{dt}}=q\Delta mc^2(1-\alpha),$

gde $\Delta m=4m_{\rm H}-m_{\rm He}$ -- defekt mass, a $\alpha$ -- dolya energii, unosimoi neitrino ( $\alpha\sim0,05\div0,1$ ).No est' i drugoi put' rozhdeniya neitrino -- urka-process, vpervye rassmotrennyi Gamovym i Shenbergom.

Pust' imeetsya stabil'noe yadro ${}^{3}{\mathrm{He}}$ . Yadro s tem zhe yadernym vesom -- yadro tritiya -- neustoichivo i raspadaetsya po sheme $\beta$ -raspada,

$\displaystyle {}^{3}{\mathrm{H}}\to {}^{3}{\mathrm{He}}+e^-+\widetilde{\nu}$

s periodom poluraspada (vremya zhizni) 12 let. Pri etom vydelyaetsya energiya $\sim$ 18 keV. Kogda mozhet idti obratnyi process

$\displaystyle e^-+ {}^{3}{\mathrm{He}}\to {}^{3}{\mathrm{H}}+\nu?$

Yasno, chto energiya elektrona dolzhna byt' bol'she 18 keV. Skorost' etogo processa

proporcional'na $E^2_{\nu}=(E-18\;$ keV

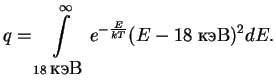
$\displaystyle q=\int\limits^{\infty}_{18\;\mbox{keV}}e^{-{E\over{kT}}}(E-18\;\mbox{keV})^2 dE.$

Glavnuyu rol' igraet eksponencial'nyi mnozhitel' $\exp(-18\;$ keV, t.e. pri komnatnoi temperature v skorost' etogo processa vhodit chislo $\exp({-10^6})$ . No pri temperature poryadka 10 keV ( $\sim 10^8$ K) process mozhet idti. Odnako odnovremenno v takom veshestve tritii opyat' raspadaetsya:

$\displaystyle {}^{3}{\mathrm{H}}\to {}^{3}{\mathrm{He}}+e^-+\widetilde{\nu},$

i opyat' obrazuyutsya $\widetilde{\nu}$ . Takim obrazom, i pri pryamom i pir obratnom processe proishodyat neobratimye poteri energii za schet $\nu$ i $\widetilde{\nu}$ , t.e. nezavisimo ot togo, vydelyaetsya energiya ili net (v kazhdom otdel'nom processe), neitrino i antineitrino uhodyat. Processy takogo roda Gamov i nazval urka-processami. Poskol'ku skorost' reakcii obrazovaniya tritiya est'

, v stacionarnyh usloviyah dolzhno byt'(koncentracii oboznachaem kvadratnymi skobkami):

$\displaystyle q(T)[{}^{3}{\mathrm{He}}]={1\over{\tau}}\;[{}^{3}{\mathrm{H}}],$

gde $\tau$ -- vremya zhizni tritiya ${}^{3}{\mathrm{H}}$ . Pust' v nachale veshestvo sostoyalo tol'ko iz yader ${}^{3}{\mathrm{He}}$ s koncentraciei $[{}^{3}{\mathrm{He}}]_0$ . Togda pri nekotoroi temperature

ustanovitsya sleduyushaya stacionarnaya koncentraciya tritiya:

$\displaystyle [{}^{3}{\mathrm{H}}]={q(T)\over{q(T)+1/\tau}}\;[{}^{3}{\mathrm{He}}]_0.$

Veroyatnost' raspada

(1/sm $^3\cdot$ s)

$\displaystyle W={1\over{\tau}}\;[{}^{3}{\mathrm{H}}]={1\over{\tau}}\;[{}^{3}{\mathrm{He}}]_0\;{1\over{1+1/\tau q}}.$

Na pervyi vzglyad kazhetsya, chto skorost' urka-processa vyhodit na konstantu (plato) pri $T\longrightarrow\infty$ ( $q\longrightarrow\infty$ pri $T\longrightarrow\infty$ ) iz-za ogranicheniya periodom poluraspada tritiya (ris. 49).

Pri vysokih temperaturah, kogda uzhe net yader, urka-process idet takim obrazom:

$\displaystyle e^-+ p=n+\nu,$

$\displaystyle n\to p+e^-+\widetilde{\nu}.$

Ris. 49.

Neitron tyazhelee protona na 0,8 MeV. Poetomu plato s dostigalos' by pri MeV. Odnako Pinaev zametil, chto pri takih temperaturah poyavlyayutsya pozitrony i nachinaet effektivno idti process

$\displaystyle e^++n\to p+\widetilde{\nu}\qquad (T>10^{10}\;$ K $\displaystyle ).$

Vsledstvie etogo chislo neitronov priblizitel'no ravno chislu protonov (bez ucheta pozitronov byli by tol'ko neitrony). Yasno, chto pri etom plato ischezaet i krivaya

idet vverh.

Vypishem bez rascheta velichinu energopoter', svyazannyh s obsuzhdaemymi processami:

$\displaystyle Q\simeq8\cdot 10^{11}\rho T^6_9=8\cdot 10^{-43}\rho T^6\;[$ erg/sm $\displaystyle \cdot$ sm $\displaystyle ^3].$

V plotnost' veshestva $\rho$ pri vysokoi temperature glavnyi vklad dayut neitrony i protony^7.2. Ob'yasnim teper', pochemu skorost' energeticheskih poter' proporcional'na

. Vo-pervyh, pri $kT\gg m_ec^2$ koncentracii elektronov i pozitronov primerno ravny i proporcional'ny

(poskol'ku massoi

mozhno prenebrech', ih impul's $p=E/c\sim kT/c\sim T$ , a koncentraciya $n\sim p^3\sim T^3$ ). Vo-vtoryh, sechenie reakcii $\sigma_{e^{-}p}=\sigma_{e^{+}n}\sim T^2$ . V obshei teorii (sm. razdel 5.4) $\sigma\sim (H')^2dN/dE$ , gde

-- matrichnyi element, kotoryi postoyanen, tak kak eto tochechnoe vzaimodeistvie, a $N=4/3\pi P^3/(2\pi\hbar)^3$ -- chislo vozmozhnyh sostoyanii s impul'som men'she

v edinice ob'ema. Ispol'zuya sootnoshenie

$\displaystyle E^2=(m_ec^2)^2+c^2p^2,$

imeem

$\displaystyle E\;dE=c^2p\;dp$

$\displaystyle dN\sim p^2\;dp\sim p\;E\;dE,$

t.e.

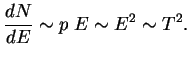
$\displaystyle {dN\over{dE}}\sim p\;E\sim E^2\sim T^2.$

Kazhdoe neitrino unosit s soboi energiyu $E_{\nu}\sim T$ . Poetomu okonchatel'no

Ris. 50.

$\displaystyle Q\sim n\sigma E_{\nu}\sim T^3\, T^2\, T=T^6.$

U nekotoryh yader mozhet nastupit' nasyshenie, a zatem uzhe stepennoi rost (ris. 50). Sushestvovanie urka-processov nesomnenno. Krome etogo est' eshe processy drugogo tipa s uchastiem neitrino, svyazannye s gipotezami, kotorye poka ne provereny eksperimental'no.

Dlya ob'yasneniya vseh eksperimental'nyh proyavlenii slabyh vzaimodeistvii do nedavnego vremeni dostatochno bylo schitat', chto vse chasticy vzaimodeistvuyut v odnoi tochke (prichem vzaimodeistvuyut -- eto znachit i rozhdayutsya). Naprimer:

$\displaystyle e^-+p=n+\nu_e.$

Mozhno schitat',chto v etom processe v odnu tochku prihodyat dve chasticy, iz toi zhe tochki vyletayut dve novye chasticy. Veroyatnost' etogo processa opisyvaetsya matrichnym elementom gamil'toniana (sm. razdel 5.4)

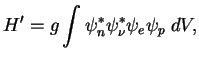
$\displaystyle H'=g\int\psi^*_n\psi^*_{\nu}\psi_e\psi_{p}\;dV,$

gde $g=1,4\cdot10^{-49}\;$ erg $\cdot$ sm

-- postoyannaya slabogo vzaimodeistviya. My zapishem samuyu sushestvennuyu chast' gamil'toniana simvolicheski sleduyushim obrazom:

$\displaystyle H=(\widetilde{p}n)\;(\widetilde{e}\nu_e)+(p\widetilde{n})\;(e\widetilde{\nu_e}).$

(7.2)

Zdes' znak $\sim$ (til'da) oboznachaet antichasticu, a skobki ob'edinyayut chasticy, vhodyashie v reakciyu vsegda po odnu storonu ot strelochki. Zapis' (2) rasshifrovyvaetsya tak: esli vstrechaetsya simvol nekotoroi chasticy, to eto oboznachaet gibel' dannoi chasticy, libo rozhdenie ee antichasticy. Naprimer, pervyi chlen v (2) simvoliziruet reakciyu

$\displaystyle \widetilde{p}+n\to e^-+\widetilde{\nu_e}$

(annigilyaciya nuklonov), a takzhe:

$\displaystyle n\to p+e^-+\widetilde{\nu_e}\qquad (\beta$ -raspad neitrona $\displaystyle ),$

a vtoroi, sopryazhennyi chlen, simvoliziruet obratnye processy

$\displaystyle p+e^-\to n+\nu_e\qquad($ neitronizaciya $\displaystyle ),$

$\displaystyle p+\widetilde{n}\to e^++\nu_e\qquad($ annigilyaciya $\displaystyle ).$

V deistvitel'nosti est' eshe reakcii s myuonom $\mu$ i myuonnym neitrino $\nu_{\mu}$ , naprimer, raspady

$\displaystyle \mu^-\to e^-+\widetilde{\nu_e}+\nu_{\mu},$

$\displaystyle \mu^+\to e^++\nu_e+\widetilde{\nu_{\mu}},$

ili zahvat myuona nuklonom:

$\displaystyle \mu^-+p\to n+\nu_{\mu}$

i t.d. Vse eti processy mozhno opisat' gamil'tonianom $H=g\,[(\widetilde{p}n)\; (\widetilde{e}\nu_e)+(\widetilde{p}n)(\widetilde{\mu}\nu_{\mu})+(\widetilde{\mu}\nu_{\mu}) (\widetilde{e}\nu_e)+$ sopryazhennye chleny

. Vse oni harakterizuyutsya konstantoi $g=1,4\cdot10^{-49}$ erg $\cdot$ sm

. Tot fakt, chto eta konstanta razmerna, predstavlyaetsya udivitel'nym. On mozhet oznachat', chto process slabogo vzaimodeistviya ne yavlyaetsya elementarnym i na samom dele protekaet v dva etapa s obrazovaniem promezhutochnoi chasticy, kotoruyu poka ne nablyudali:

$\displaystyle n\to p+W^-,\qquad W^-\to e^-+\widetilde{\nu_e}.$

Iz sohraneniya momenta yasno, chto eta chastica dolzhna imet' spin

, t.e. dolzhna byt' bozonom. Processy s

-bozonom analogichny elektromagnitnym processam s fotonom:

$\displaystyle p\to p+\gamma,\quad \gamma\to e^-+e^+.$

Teoriya

-bozona predpolagaet, chto on vo vsem, krome bol'shoi massy, pohozh na foton. V etom sluchae elementarnye vzaimodeistviya s

-bozonom harakterizuyutsya toi zhe bezrazmernoi konstantoi, chto i elektromagnitnoe vzaimodeistvie (postoyannoi tonkoi struktury):

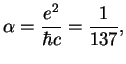
$\displaystyle \alpha={e^2\over{\hbar c}}={1\over{137}},$

a ``slabost''' slabogo vzaimodeistviya ob'yasnyaetsya tem, chto pri obychnyh energiyah

-bozon poyavlyaetsya tol'ko virtual'no iz-za svoei bol'shoi massy. Znachenie massy

-bozona

mozhno ocenit' iz eksperimental'nogo znacheniya postoyannoi slabogo vzaimodeistviya

i razmernyh soobrazhenii:

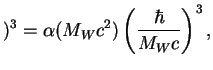
$\displaystyle g=\alpha\cdot$ energiya $\displaystyle \cdot($ dlina $\displaystyle )^3=\alpha(M_Wc^2)\left({\hbar\over {M_Wc}}\right)^3,$

otkuda

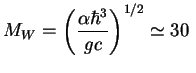$\displaystyle M_W=\left({\alpha\hbar^3\over{gc}}\right)^{1/2}\simeq 30\;$ GeV $\displaystyle \simeq 30\;m_{p}.$

Rasstoyanie, kotoroe prohodit -bozon do raspada, mozhno ocenit' iz sootnosheniya neopredelennostei

$\displaystyle x\sim \hbar/M_Wc\simeq 10^{-15}\;$ sm $\displaystyle .$

Malost' etogo rasstoyaniya (na dva poryadka men'she radiusa yadernyh sil!) i pozvolyala staroi teorii schitat' slaboe vzaimodeistvie tochechnym.

Kvantovomehanicheskaya amplituda processov s rozhdeniem -bozona dolzhna imet' vid

$\displaystyle J=(\widetilde{p}n)\widetilde{W}+(e\widetilde{\nu_e})\widetilde{W} +(\mu\widetilde{\nu_{\mu}})\widetilde{W}.$

Po obshim principam kvantovoi mehaniki polnaya amplituda processov, idushih cherez promezhutochnyi

-bozon, ravna proizvedeniyu amplitudy obrazovaniya,

, na amplitudu raspada

, kotoraya, ochevidno, ravna

, t.e. sopryazhenna

$\displaystyle J^*=W(p\widetilde{n})+W(\widetilde{e}\nu_e)+W(\widetilde{\mu}\nu_{\mu}).$

Gamil'tonian nablyudaemyh processov togda vyglyadit sleduyushim obrazom:

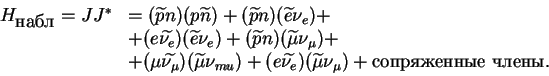
$\begin{displaymath} \begin{array}{ll} H_{\mbox{nabl}}=JJ^*&=(\widetilde{p}n)(p\w... ...etilde{\mu}\nu_{\mu}) +\mbox{sopryazhennye chleny.}\cr \end{array}\end{displaymath}$

Proizvedenie $\widetilde{W}W$ , oboznachayushee rozhdenie i gibel'

, voidet prosto v konstantu slabogo vzaimodeistviya

, kotoruyu my opuskaem v simvolicheskoi zapisi gamil'toniana. Processy, stoyashie v pravom stolbce etogo vyrazheniya, davno uzhe nablyudalis' v laboratorii. V poslednee vremya obnaruzheny i processy, zapisannye v levom stolbce.

Process $(\widetilde{p}n)(p\widetilde{n})$ , t.e. $p+n\rightleftarrows p+n$ -- eto rasseyanie nuklonov za schet slabogo vzaimodeistviya. Ego nablyudat' trudno, tak kak est' rasseyanie za schet sil'nogo vzaimodeistviya. No slaboe vzaimodeistvie privodit k nesohraneniyu chetnosti, i v etih processah, naprimer, dolzhny poyavlyat'sya $\gamma$ -kvanty s krugovoi polyarizaciei.

Process $(e\widetilde{\nu_e})(\widetilde{e}\nu_e)$ -- rasseyanie neitrino na elektronah:

$\displaystyle e^-+\nu_e\rightleftarrows e^-+\nu_e.$

My mozhem perestavlyat' chasticy sprava nalevo s zamenoi ih na antichasticy:

$\displaystyle e^-+e^+\rightleftarrows \nu_e+\widetilde{\nu_e},$

$\displaystyle e^+\rightleftarrows e^-+\nu_e+\widetilde{\nu_e}.$

Process

$\displaystyle e^-+\nu_e\rightleftarrows e^-+\nu_e$

nablyudat' ochen' trudno, gorazdo slozhnee processa $\nu_e+p\rightleftarrows n+e^+$ , kotoryi uzhe nablyudalsya.

Interesno, chto Raines v svoe vremya dal dlya processa $(e\widetilde{\nu_e})(\widetilde{e}\nu_e)$ eksperimental'noe znachenie secheniya $\sigma_{\mbox{eksp}}=500\;\sigma_{\mbox{teor}}$ , no eto okazalos' oshibkoi. Seichas

$\displaystyle \sigma_{\mbox{eksp}}=(1\pm 1)\,\sigma_{\mbox{teor}}.$

Esli by bylo $\sigma_{\mbox{eksp}}=500\;\sigma_{\mbox{teor}}$ , to etogo ne dopustila by astrofizika.

Process

$\displaystyle e^-\to e^-+\nu+\widetilde{\nu}$

ne idet na svobodnom elektrone po zakonam sohraneniya. On idet v pole yadra:

$\displaystyle e^-+Z\to Z+e^-+\nu+\widetilde{\nu}$

i unosit energiyu, tak kak $\nu\widetilde{\nu}$ uletayut.

Esli ``raskachivat''' kusok veshestva, to elektromagnitnye volny on izluchat' ne budet, tak kak veshestvo elektroneitral'no, no dannyi neitrinnyi process mozhet idti, tak kak on ne kompensiruetsya protonami, t.e. pri kolebanii veshestva voznikaet neitrinnoe izluchenie.

Dannyi vid vzaimodeistviya privodit k tomu, chto mezhdu lyubymi dvumya telami est' dal'nodeistvuyushaya sila, potencial kotoroi proporcionalen $\varphi=1/r^5$ .

V gamil'toniane est' chlen

$\displaystyle g(e\widetilde{\nu_e})(\widetilde{e}\nu_e),$

gde $g=1,4\cdot10^{-49}$ erg $\cdot$ sm

-- konstanta slabogo vzaimodeistviya, t.e. energiya neitrino zavisit ot plotnosti elektronov v dannom meste. Potencial'naya yama, rasschitannaya na odno neitrino, sostavit (dlya svinca)

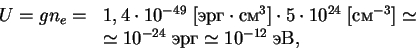
$\begin{displaymath} \begin{array}{ll} U=gn_e=&1,4\cdot10^{-49}\;[\mbox{erg}\cdot... ...q10^{-24}\;\mbox{erg}\simeq 10^{-12}\;\mbox{eV},\cr \end{array}\end{displaymath}$

t.e. poyavlyaetsya koefficient prelomleniya veshestva dlya neitrino.

Est' i drugie processy s izlucheniem neitrino. Eto plazmennye kolebaniya s ispuskaniem neitrinno-antineitrinnyh par. Na stadii goreniya ugleroda neitrinnoe izluchenie mozhet byt' ravno fotonnomu.

Nakonec, pri vysokoi temperature ( $T>10^{10}$ K) samym glavnym stanovitsya process $e^++e^-\to\nu+\widetilde{\nu}$ (on ostaetsya sravnimym s urka-processom Pinaeva).

Pary $\nu\widetilde{\nu}$ v etom processe rozhdayutsya s veroyatnost'yu gorazdo men'shei, chem pary $\gamma$ -kvantov v processe

$\displaystyle e^+e^-\to\gamma+\gamma,$

no poslednii process idet v pryamuyu i obratnuyu storony i ne vliyaet na veroyatnost' pervogo. Pri ochen' vysokih temperaturah skorost' energopoter' opredelyaetsya vyrazheniem

$\displaystyle Q\sim4\cdot10^{15}\cdot T^9_9\;[$ erg/s $\displaystyle \cdot$ sm $\displaystyle ^3].$

Legko ponyat', otkuda poyavilas' vysokaya -- devyataya stepen' temperatury:

$\displaystyle Q\sim n_{e^-}n_{e^+}\sigma E\sim T^3\,T^3\,T^2\,T=T^9.$

Pri nizkoi temperature

$\displaystyle n_{e^-}n_{e^+}\equiv[e^+][e^-]\sim\exp(-2m_ec^2/kT)\sim e^{-12/T_9}.$

Otmetim principial'no novye rezul'taty semidesyatyh godov v oblasti slabogo vzaimodeistviya i ih astrofizicheskoe znachenie.

V 1974 g. byl otkryt tretii chlen ryada, pervye dva kotorogo predstavlyayut soboi elektron i myuon. Eta chastica oboznachaetsya $\tau$ i nazyvaetsya tau-lepton. Fizika vstupaet v protivorechie s filologiei: lepton po-grecheski znachit ``legkii'', i eto bylo pravil'no primenitel'no k $e^{\pm}$ i $\mu^{\pm}$ . Massa $\tau$ ravna 1780 MeV, t.e. on v 1,9 raza tyazhelee protona, legkim ego nazvat' nel'zya. No svoistva $\tau$ podobny svoistvam i $\mu$ . Poetomu, pridavaya slovu ``lepton'' novyi smysl -- ``fermion, obladayushii slabym i elektromagnitnym, no ne sil'nym, vzaimodeistviyami'', my nazyvaem $\tau$ leptonom. Predpolagaetsya, chto sushestvuet i sootvetstvuyushee etomu leptonu neitrino, $\nu_{\tau}$ , a takzhe ego antichastica $\widetilde{\nu_{\tau}}$ , podobno tomu kak myuonu sootvetstvuet $\nu_{\mu}$ i $\widetilde{\nu_{\mu}}$ . Sledovatel'no, raspady $\tau$ idut tak: $\tau^-=\mu^-+\nu_{\tau}+\widetilde{\nu_{\mu}}$ ili $\tau^+=\pi^++\nu_{\tau}$ . Raspad s obrazovaniem pionov i drugih adronov nevozmozhen dlya myuona, no vozmozhen dlya tau-leptona blagodarya bol'shoi masse etoi chasticy.

Vtoroe otkrytie -- sushestvovanie neitral'nogo toka. Processy, protekayushie cherez posredstvo promezhutochnyh bozonov $W^{\pm}$ , nazyvayut zavisimymi ot zaryazhennogo toka. Fenomenologicheski eti processy zapisany tak, chto kazhdyi chlen v vyrazhenii dlya toka (v nashih oboznacheniyah dlya amplitudy ) menyaet zaryad na edinicu, a obshii zaryad sohranyaetsya, potomu chto gamil'tonian soderzhit proizvedenie dvuh tokov, odnogo umen'shayushego i drugogo uvelichivayushego zaryad. No v teorii Salama-Veinberga predpolagaetsya, chto naryadu s $W^{\pm}$ sushestvuet analogichnyi tyazhelyi vektornyi (spin 1) promezhutochnyi (v slabom vzaimodeistvii) i pritom neitral'nyi bozon. Buduchi neitral'nym, on dolzhen raspadat'sya na pary neitrino-antineitrino ili pary zaryazhennyh chastic ili antichastic: $Z^0\rightleftarrows \nu_e+\widetilde\nu_e$ , $Z^0\rightleftarrows e^++e^-\ldots$ Analogichno etomu proishodit i vzaimodeistvie s adronami^7.3. Kak vsegda v takih formulah mozhno perenesti antichasticu sprava nalevo, prevrashaya ee v chasticu. U samogo -bozona net antichasticy, ili tochnee on sam yavlyaetsya svoei antichasticei, tak kak istinno neitralen, takzhe kak foton.

Na opyte pri energiyah, nedostatochnyh dlya real'nogo rozhdeniya -bozona (takaya situaciya prodlitsya veroyatno do 1985 g.), nablyudayutsya processy tipa rasseyaniya: $\nu_{\mu}+p\to Z^0\to\nu_{\mu}+p$ . Predskazyvaetsya takzhe slaboe vzaimodeistvie elektronov s yadrami, kotoroe obnaruzhivaetsya pri rasseyanii relyativistskih elektronov, a takzhe v opticheskom povedenii atomov. Eto vzaimodeistvie kachestvenno bylo predskazano odnim iz avtorov (Ya.B.Zel'dovichem) eshe v 1958 g. V nastoyashee vremya ego mozhno schitat' dokazannym.

Kakovy astrofizicheskie sledstviya sushestvovaniya neitral'nogo toka?

S odnoi storony, rasshiryayutsya vozmozhnosti proizvodstva par neitrino-antineitrino. Teper' vozmozhny processy

$\displaystyle e^-+e^+\to Z^0\to\nu_{\mu}+\widetilde{\nu_{\mu}},$

$\displaystyle e^-+e^+\to Z^0\to\nu_{\tau}+\widetilde{\nu_{\tau}}.$

Vozmozhno takzhe rozhdenie par $\nu,\;\widetilde{\nu}$ pri stolknovenii adronov ili vozbuzhdennymi sostoyaniyami yader $A^*\to A+Z^0\to A+\nu+\widetilde{\nu}$ ( $\nu_e$ , $\nu_{\mu}$ , $\nu_{\tau}$ -- s odinakovoi veroyatnost'yu). S drugoi storony, poyavlyaetsya novyi kanal rasseyaniya neitrino na elektronah i , glavnoe, novyi process rasseyaniya neitrino na yadrah. V etom processe rasseyanie na vseh nuklonah mozhet proishodit' kogerentno, pri etom amplituda rasseyannoi volny proporcional'na chislu nuklonov, a sechenie rasseyaniya okazyvaetsya proporcional'no kvadratu chisla nuklonov. Takim obrazom uvelichivaetsya neprozrachnost' plotnogo veshestva, sostoyashego iz tyazhelyh i srednih yader po otnosheniyu k neitrino vseh sortov. Etot fakt igraet bol'shuyu rol' v teorii vzryva sverhnovyh zvezd.

Kakova rol' neitrinnyh processov v evolyucii zvezd voobshe? Na stadii glavnoi posledovatel'nosti neitrinnoe izluchenie, kazalos' by, malosushestvenno. Odnako nel'zya zabyvat', chto, vo-pervyh, bez slabogo vzaimodeistviya, a znachit i bez izlucheniya neitrino, voobshe ne vozmozhno gorenie vodoroda. A, vo-vtoryh, neitrino pozvolyaet v principe zaglyanut' v samye central'nye oblasti zvezd i proverit' nashi teorii. Dlya Solnca eto uzhe delaetsya (opyty Devisa).

Na pozdnih stadiyah evolyucii neitrinnoe izluchenie mozhet igrat' reshayushuyu rol', poskol'ku dostigayutsya vysokie temperatury, i neitrino effektivno otvodit teplo. Bez neitrino trudno ob'yasnit' obrazovanie planetarnyh tumannostei, vzryvy sverhnovyh. Neitrinnoe izluchenie sil'no uskoryaet ostyvanie goryachih belyh karlikov i neitronnyh zvezd. Poetomu, sravnivaya predskazaniya teorii evolyucii zvezd, rasschitannye s uchetom i bez ucheta neitrino, s nablyudeniyami real'nyh ob'ektov, mozhno proverit' teoriyu slabyh vzaimodeistvii, t.e. ustanovit' nalichie v prirode teh processov, kotorye v laboratorii poka ne nablyudalis'.

<< 7.3 Dva tipa energeticheskih ... | Oglavlenie | 8. Vvedenie v OTO >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce