<< 8. Vvedenie v OTO | Oglavlenie | 8.2 Parallel'nyi perenos vektorov >>
8.1 Ideya iskrivlennogo prostranstva-vremeni
Vse tela nezavisimo ot ih massy padayut s odinakovym uskoreniem -- eto bylo izvestno so vremen Galileya. No imenno etot fakt stal opredelyayushim dlya Einshteina pri sozdanii obshei teorii otnositel'nosti (OTO). Zakon tyagoteniya N'yutona ochen' pohozh na zakon Kulona. Odnako v zakon N'yutona v kachestve gravitacionnogo zaryada vhodit velichina, proporcional'naya inertnoi masse. Pochemu zhe tyagoteniya svyazano s inertnoi massoi? S tochki zreniya n'yutonovskoi teorii eto nekotoraya sluchainost'. Odnako imenno ot etogo ottolknulsya Einshtein, kogda emu prishla v golovu ideya iskrivlennogo prostranstva.
V ploskom chetyrehmernom prostranstve (
![]() ) dvizheniyu po pryamoi sootvetstvuet
ravnomernoe pryamolineinoe dvizhenie. V ploskom prostranstve pryamaya -- eto kratchaishee
rasstoyanie mezhdu dvumya tochkami, t. e. ekstremal'. Ideya Einshteina zaklyuchaetsya v tom, chto
i v pole tyagoteniya vse tela dvizhutsya po ekstremal'nym (geodezicheskim) liniyam v
prostranstve-vremeni, kotoroe, odnako, uzhe ne ploskoe, a iskrivlennoe. Prostranstvo-vremya
iskrivlyayut massy, sozdayushie pole tyazhesti. Esli prostranstvo iskrivleno, i vse tela dvizhutsya
po geodezicheskim, to eto oznachaet, chto tela raznoi prirody budut dvigayutsya po odinakovym traektoriyam, t. e.
estestvenno ob'yasnyaetsya nezavisimost' uskoreniya svobodnogo padeniya ot prirody tela.
) dvizheniyu po pryamoi sootvetstvuet
ravnomernoe pryamolineinoe dvizhenie. V ploskom prostranstve pryamaya -- eto kratchaishee
rasstoyanie mezhdu dvumya tochkami, t. e. ekstremal'. Ideya Einshteina zaklyuchaetsya v tom, chto
i v pole tyagoteniya vse tela dvizhutsya po ekstremal'nym (geodezicheskim) liniyam v
prostranstve-vremeni, kotoroe, odnako, uzhe ne ploskoe, a iskrivlennoe. Prostranstvo-vremya
iskrivlyayut massy, sozdayushie pole tyazhesti. Esli prostranstvo iskrivleno, i vse tela dvizhutsya
po geodezicheskim, to eto oznachaet, chto tela raznoi prirody budut dvigayutsya po odinakovym traektoriyam, t. e.
estestvenno ob'yasnyaetsya nezavisimost' uskoreniya svobodnogo padeniya ot prirody tela.
Chto takoe iskrivlennoe prostranstvo? Proshe vsego eto ponyat' na primere dvumernogo
sluchaya. Rassmotrim poverhnost' shara
![]() . ``Pryamymi'' na etoi poverhnosti budut
dugi bol'shogo kruga, tak kak im sootvetstvuyut kratchaishie rasstoyaniya na poverhnosti. Summa uglov
treugol'nika uzhe ne ravna
. ``Pryamymi'' na etoi poverhnosti budut
dugi bol'shogo kruga, tak kak im sootvetstvuyut kratchaishie rasstoyaniya na poverhnosti. Summa uglov
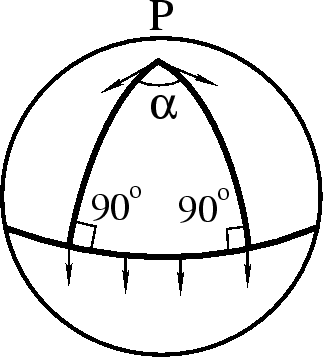
treugol'nika uzhe ne ravna ![]() . Rassmotrim treugol'nik s vershinoi v polyuse i dvumya
vershinami na ekvatore (ris. 51).
Summa uglov v etom treugol'nike ravna
. Rassmotrim treugol'nik s vershinoi v polyuse i dvumya
vershinami na ekvatore (ris. 51).
Summa uglov v etom treugol'nike ravna
![]() .
Ploshad' treugol'nika ravna
.
Ploshad' treugol'nika ravna
![]() .
.
V dvumernom sluchae mozhno predstavit' krivoe prostranstvo vlozhennym v trehmernoe
prostranstvo. Odnako prostranstvo dannoi razmernosti mozhno izuchat' i neposredstvenno, po
vnutrennim svoistvam, ne obrashayas' k idee vlozheniya. Naprimer, tochki poverhnosti shara
mozhno harakterizovat' dvumya nezavisimymi koordinatami ![]() i
i ![]() (shirotoi i dolgotoi).
Mozhno naiti vyrazhenie dlya elementa dliny na poverhnosti shara
(shirotoi i dolgotoi).
Mozhno naiti vyrazhenie dlya elementa dliny na poverhnosti shara
Dlya elementa dliny v ploskom dvumernom prostranstve mozhno zapisat'
Itak, otlichie krivoi poverhnosti ot ploskoi mozhno obnaruzhit', issleduya geometriyu samoi dvumernoi poverhnosti, bez vlozheniya.
Obratimsya k trehmernomu sluchayu.
V ploskom prostranstve kvadrat elementa dliny ![]() mezhdu dvumya beskonechno blizkimi
tochkami zapisyvaetsya v vide (
mezhdu dvumya beskonechno blizkimi
tochkami zapisyvaetsya v vide (
![]() -- sootvetstvuyushie raznosti koordinat)
-- sootvetstvuyushie raznosti koordinat)
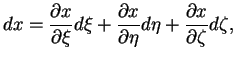
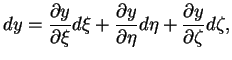
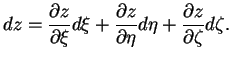
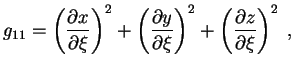
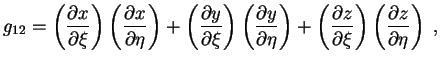
Poka my tol'ko lish' v novom vide opisali ploskoe prostranstvo. Imeem 9 velichin
![]() , iz kotoryh tol'ko 6 nezavisimy, tak kak
, iz kotoryh tol'ko 6 nezavisimy, tak kak
![]() . Mozhno pokazat',
chto v ploskom prostranstve sami velichiny
. Mozhno pokazat',
chto v ploskom prostranstve sami velichiny ![]() , ih pervye i vtorye proizvodnye
opredelennym obrazom svyazany. Umesten vopros, chto budet, esli vybrat'
, ih pervye i vtorye proizvodnye
opredelennym obrazom svyazany. Umesten vopros, chto budet, esli vybrat' ![]() ,
chtoby eti svyazi ne vypolnyalis'? Togda okazhetsya, chto takaya metrika opisyvaet
iskrivlennoe prostranstvo, kotoroe uzhe trudno predstavit' naglyadno.
Pri etom
,
chtoby eti svyazi ne vypolnyalis'? Togda okazhetsya, chto takaya metrika opisyvaet
iskrivlennoe prostranstvo, kotoroe uzhe trudno predstavit' naglyadno.
Pri etom ![]() opredelyayut kak koordinatnuyu setku, tak i kriviznu prostranstva.
opredelyayut kak koordinatnuyu setku, tak i kriviznu prostranstva.
Zdes' umestno sdelat' istoricheskoe zamechanie: Lobachevskii i Bol'yai rassmatrivali prostranstvo, krivizna kotorogo vezde postoyanna. Ne vyrazhaya etoi mysli v yavnom vide, oni ishodili iz idei, chto sushestvuyut absolyutno zhestkie tela. Takoe telo mozhet peremeshat'sya v prostranstve postoyannoi krivizny.
Harakterizuya prostranstvo metricheskimi koefficientami ![]() , yavlyayushimisya proizvol'nymi funkciyami
koordinat, Riman vvel v rassmotrenie prostranstvo, krivizna kotorogo menyaetsya ot tochki k tochke.
V etot zhe period voznikayut pervye idei o tom, chto krivizna prostranstva mozhet byt'
svyazana s fizicheskimi faktorami. Otkaz ot idei absolyutno zhestkogo tela stal vpolne estestvennym
pozzhe, s razvitiem elektronnoi teorii i otkrytiem lorenceva sokrasheniya tel.
, yavlyayushimisya proizvol'nymi funkciyami
koordinat, Riman vvel v rassmotrenie prostranstvo, krivizna kotorogo menyaetsya ot tochki k tochke.
V etot zhe period voznikayut pervye idei o tom, chto krivizna prostranstva mozhet byt'
svyazana s fizicheskimi faktorami. Otkaz ot idei absolyutno zhestkogo tela stal vpolne estestvennym
pozzhe, s razvitiem elektronnoi teorii i otkrytiem lorenceva sokrasheniya tel.
V iskrivlennom prostranstve mozhno opredelyat' krivuyu, dayushuyu minimum rasstoyaniya mezhdu dvumya tochkami:
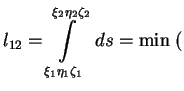 po vsem putyam
iz 1 v 2
po vsem putyam
iz 1 v 2V obshem sluchae iskrivlennogo prostranstva takoi prostoi zavisimosti ne budet; mozhno napisat' tol'ko differencial'nye uravneniya -- uravneniya geodezicheskoi.
Nakonec, sleduyushii shag zaklyuchaetsya v tom, chto rassmatrivaetsya kak ishodnoe, chetyrehmernoe prostranstvo Minkovskogo, ili, drugimi slovami, kompleks, sostoyashii iz vremeni i trehmernogo prostranstva (v uzkom smysle slova).
Eto chetyrehmernoe mnogoobrazie preobrazuetsya po Lorencu, a ne po Galileyu, t. e. tak, chto ostaetsya invariantnym
<< 8. Vvedenie v OTO | Oglavlenie | 8.2 Parallel'nyi perenos vektorov >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |