Astronet > 8.3 Fizika iskrivlennogo prostranstva-vremeni

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 8.2 Parallel'nyi perenos vektorov | Oglavlenie | 8.4 Gravitacionnoe krasnoe smeshenie... >>

8.3 Fizika iskrivlennogo prostranstva-vremeni

V otsutstvie gravitacionnogo polya fizika razvorachivaetsya v psevdoevklidovom prostranstve Minkovskogo s metrikoi

$\displaystyle ds^2=c^2dt^2-dx^2-dy^2-dz^2.$

Pri nalichii gravitacii, t. e. v OTO, budem schitat', chto prostranstvo iskrivleno:

$\displaystyle ds^2=g_{ik}(x)\,dx^idx^k,\;\;g_{ik}=g_{ki}$

(8.1)

(po povtoryayushimsya indeksam predpolagaetsya summirovanie).

Esli zadan metricheskii tenzor $g_{ik}$ (dlya kratkosti budem govorit' ``metrika'' $g_{ik}$ ),to mozhno naiti geodezicheskie v prostranstve-vremeni, t. e. opredelit' dvizhenie chastic v gravitacionnom pole.

V dannoi tochke kvadratichnuyu formu (1) mozhno diagonalizovat' i privesti ee k metrike Minkovskogo^8.2.

V obshem sluchae mozhno razlozhit' $g_{ik}$ v ryad Teilora v okrestnosti tochki

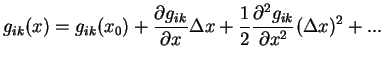
$\displaystyle g_{ik}(x)=g_{ik}(x_0)+{\partial g_{ik}\over{\partial x}}\Delta x+{1\over 2} {\partial^2 g_{ik}\over{\partial x^2}}(\Delta x)^2+...$

Preobrazovaniem sistemy koordinat v dannoi tochke vsegda mozhno obratit' v nul' pervye proizvodnye $g_{ik}$ . Dlya etogo dostatochno pereiti v svobodno padayushuyu sistemu otscheta. No proizvol'nuyu sovokupnost' vseh vtoryh proizvodnyh $g_{ik}$ nikakimi preobrazovaniyami sistemy koordinat unichtozhit' nel'zya.

Esli rassmatrivat' kvadratichnye effekty, naprimer, otnositel'nye uskoreniya udalennyh chastic, to mozhno zametit' prilivnye sily. Nevesomost' sushestvuet lish' esli ogranichit'sya pervym poryadkom po $\Delta x$ . Takim obrazom, odna chastica ``ne chuvstvuet'' gravitacionnogo polya, no sistema s raznesennymi massami ``chuvstvuet''. Global'no gravitacionnoe pole vsegda mozhno obnaruzhit'.

Takim obrazom, v chlenah pervogo poryadka po $\Delta x$ effekt gravitacii kompensiruetsya uskoreniem svobodnogo padeniya -- v etom i sostoit tochnaya formulirovka principa ekvivalentnosti. (Bolee grubaya formulirovka: ``Sily inercii ekvivalentny nekotoromu polyu tyagoteniya''.)

Itak, krivizna prostranstva harakterizuetsya dvadcat'yu nezavisimymi chislami $R^i_{klm}$ . Estestvenno svyazat' $R^i_{klm}$ s veshestvom.

V n'yutonovskoi teorii potencial gravitacionnogo polya opredelyaetsya plotnost'yu veshestva $\rho\,$ [g/sm]. Mozhno perevesti plotnost' veshestva $\rho$ v plotnost' energii $\varepsilon=\rho c^2$ . V special'noi teorii otnositel'nosti $\varepsilon$ yavlyaetsya 00-komponentoi tenzora energii-impul'sa

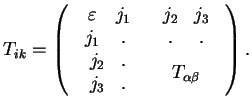
$\displaystyle T_{ik}= \left( \begin{array}{cc} \begin{array}{cc} \varepsilon & ... ...2 & . \\ j_3 & . \\ \end{array} & T_{\alpha\beta} \\ \end{array}\right).$

Tenzor $T_{ik}$ sostoit iz velichin, kotorye po otnosheniyu k trehmernym, chisto prostranstvennym povorotam vedut sebya kak skalyar $\varepsilon$ , vektor $\vec{j}$ (potok energii-impul'sa na edinicu ob'ema) i trehmernyi tenzor natyazhenii $T_{\alpha\beta}$ , diagonal'nye chleny kotorogo harakterizuyut davlenie, a nediagonal'nye -- vyazkost'.

My vidim, chto veshestvo harakterizuetsya tenzorom vtorogo ranga.

Einshtein poluchil uravneniya polya v vide

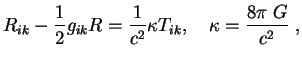
$\displaystyle R_{ik}-{1\over 2}g_{ik}R={1\over{c^2}}\kappa T_{ik},\quad \kappa={8\pi\;G\over{c^2}}\;,$

gde $R_{ik}=g^{lm}R_{limk},\;R=g^{ik}R_{ik}$ . Iz etih uravnenii sleduet (v sluchae slabyh polei) zakon tyagoteniya N'yutona i, krome togo, avtomaticheski vypolnyayutsya zakony sohraneniya^8.3.

V elektromagnitnoi teorii zaryad sohranyaetsya, no dvizhenie zaryada proizvol'no. V OTO $T_{ik}$ ne mozhet byt' lyubym -- dvizhenie dolzhno sootvetstvovat' zakonam mehaniki, t.e. zakonam sohraneniya energii i impul'sa. Net metriki, gde veshestvo snachala pokoilos', a potom vse v celom samoproizvol'no nachalo by dvigat'sya. Krome togo, okazalos', chto iz uravnenii OTO poluchayutsya ne tol'ko zakony dvizheniya material'nyh tochek (t. e. zakony mehaniki), no i (s nebol'shim proizvolom) zakony svobodnogo elektromagnitnogo polya(uravneniya Maksvella). Eto porodilo v svoe vremya massu nadezhd. Kazalos', chto vsyu fiziku mozhno vyvesti iz OTO. Odnako popytki sozdat' edinuyu teoriyu polya k uspehu ne priveli.

Chislo uravnenii Einshteina ravno chislu komponent tenzora vtorogo ranga, a polnoe opisanie prostranstva zadaetsya tenzorom chetvertogo ranga $R_{klm}^i$ . V dvumernom i trehmernom prostranstve-vremeni zadanie $R_{ik}$ odnoznachno opredelyaet $R_{klm}^i$ , v chetyrehmernom mire eto ne tak: uslovie $R_{ik}=0$ sovmestimo s $R_{klm}^i\ne 0$ . Eto oznachaet, chto gravitacionnoe pole mozhet sushestvovat' i bez istochnikov -- eto, naprimer, gravitacionnye volny.

Eshe angliiskii matematik Klifford vyskazal ideyu, chto u prostranstva dolzhna byt' sobstvennaya uprugost'. V nekotorom smysle OTO yavlyaetsya razvitiem etoi idei. V lagranzhian vhodit krivizna $R=g^{ik}R_{ik}$ :

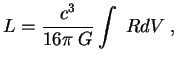
$\displaystyle L={c^3\over{16\pi \;G}}\int\;RdV\;,$

gde

-- chetyrehmernyi ob'em. (Esli zadat'sya takim lagranzhianom i lagranzhianom drugih polei i chastic, to pri var'irovanii metriki mozhno poluchit' uravneniya OTO, chto i sdelal Gil'bert.) Mozhno naglyadno predstavit' sebe, chto

opisyvaet uprugost' prostranstva, ``stremlenie'' prostranstva ostavat'sya ploskim. Konstanta $c^3/16\pi G$ , harakterizuyushaya uprugost' vakuuma, velika, i prostranstvo iskrivleno slabo, iz-za togo, chto velika ego uprugost'.

Mozhet smutit' to obstoyatel'stvo, chto konstanta $c^3/16\pi G$ razmerna, poetomu neponyatno, otnositel'no chego ona yavlyaetsya bol'shoi. V bezrazmernom vide silu gravitacionnogo vzaimodeistviya harakterizuet konstanta $Gm^2/\hbar c$ , analogichnaya konstante elektromagnitnogo vzaimodeistviya $e^2/\hbar c=1/137$ . Iz vida konstanty srazu poluchaem massu, harakternuyu dlya gravitacionnogo vzaimodeistviya (tak nazyvaemaya plankovskaya massa, sravnite analogichnye rassuzhdeniya o slabom vzaimodeistvii i o masse -bozona v razdele 7.4):

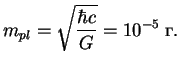
$\displaystyle m_{pl}=\sqrt{{\hbar c\over G}}=10^{-5}\;\mbox{g}.$

Harakternaya kvantovaya dlina etoi massy:

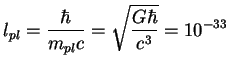$\displaystyle l_{pl}={\hbar\over{m_{pl}c}}=\sqrt{{G\hbar\over{c^3}}}=10^{-33}\;$ sm $\displaystyle .$

Legko ubeditsya, chto $l_{pl}$ sovpadaet kak raz s gravitacionnym radiusom $r_{g}$ dlya plankovskoi massy. Takim obrazom, iskrivlenie prostranstva veliko na rasstoyanii $l_{pl}$ ot massy $m_{pl}$ . Dlya izvestnyh elementarnyh chastic $m\sim 10^{-24}\,{\mbox g}\ll m_{pl}$ , $l\sim 10^{-13}\,{\mbox sm} \ll l_{pl}$ , t. e. effekty gravitacii i iskrivleniya prostranstva v ob'eme izvestnyh elementarnyh chastic chrezvychaino maly. Eto i dokazyvaet bol'shuyu uprugost' vakuuma.

Nel'zya li poluchit' uprugost' prostranstva iz kakih-to bolee obshih soobrazhenii? Iz kvantovoi teorii my znaem, chto vakuum obladaet nulevymi kolebaniyami, kotorye, v chastnosti, dayut popravki v urovnyah atoma vodoroda (Lembovskii sdvig). Mozhet byt' takie effekty privodyat i k uprugosti vakuuma? Takoi podhod udalos' sformulirovat', no pri etom okazalos', chto v teoriyu neobhodimo vvodit' chasticy s massoi $m_{pl}$ .

Takim obrazom, est' dva principial'no razlichnyh napravleniya:

1) iz teorii tyagoteniya vyvesti sushestvovanie chastic s $m_{pl}$ .

2) iz teorii chastic poluchit' konstantu . (Podrobnee sm. knigi Ya.B.Zel'dovicha i I.D. Novikova ``Relyativistskaya astrofizika'' i ``Teoriya tyagoteniya i evolyuciya zvezd'').

<< 8.2 Parallel'nyi perenos vektorov | Oglavlenie | 8.4 Gravitacionnoe krasnoe smeshenie... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce