Astronet > 8.4 Gravitacionnoe krasnoe smeshenie. Zamedlenie vremeni

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 8.3 Fizika iskrivlennogo ... | Oglavlenie | 9. Sil'nye gravitacionnye polya ... >>

8.4 Gravitacionnoe krasnoe smeshenie. Zamedlenie vremeni

V predydushih razdelah my uvideli, chto osnovnaya ideya OTO o dvizhenii tel v iskrivlennom prostranstve-vremeni po geodezicheskim oznachaet, chto vse tela padayut v gravitacionnom pole po odinakovym traektoriyam s odinakovym uskoreniem.

Ris. 53.

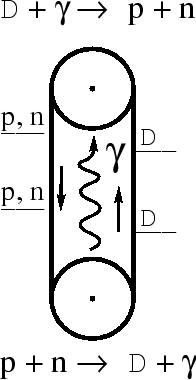
Pokazhem seichas s pomosh'yu OTO i kvantovoi mehaniki, chto v gravitacionnom pole proishodit zamedlenie vremeni. Dlya etogo rassmotrim odin proekt vechnogo dvigatelya. Na ustanovke iz dvuh blokov (ris. 53) budem podnimat' yadra deiteriya, a opuskat' protony i neitrony.

Pust' vnizu protony reagiruyut s neitronami, a obrazuyushiesya $\gamma$ -kvanty ispol'zuyutsya naverhu dlya dissociacii deiteriya. Massa na 2,2 MeV men'she , poetomu pod deistviem bol'shei tyazhesti p-n sistema budet otdavat' energiyu, sovershat' vechnoe dvizhenie.

Oshibka etogo proekta v tom, chto v deistvitel'nosti $\gamma$ -kvant ne poglotitsya, tak kak chast' ego energii uidet na preodolenie sily tyazhesti:

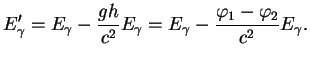
$\displaystyle E'_{\gamma}=E_{\gamma}-{gh\over{c^2}}E_{\gamma}=E_{\gamma}-{\varphi_1-\varphi_2\over{c^2}} E_{\gamma}. %% izmenil znak! \varphi$

Energiya $\gamma$ -kvanta $E_\gamma=\hbar \omega$ . Poskol'ku $E'_{\gamma}<E_{\gamma}$ , to $\omega'<\omega$ , t. e. chastota fotonov ispytyvaet krasnoe smeshenie v gravitacionnom pole. Etot effekt uzhe nablyudalsya na Zemle s pomosh'yu effekta Messbauera (opyt Paunda i Rebki).

V obshem sluchae mozhno napisat'

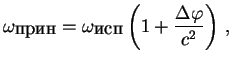
$\displaystyle \omega_{\mbox{prin}}=\omega_{\mbox{isp}}\left(1+\frac{\Delta\varphi}{c^2}\right)\,,$

gde $\Delta\varphi$ -- razlichie gravitacionnogo potenciala v mestah ispuskaniya i priema. Eto sootnoshenie verno dlya fotonov lyubyh chastot. V dannom meste chastota fotonov zavisit tol'ko ot svoistv ispuskayushih ih atomov (ili yader). Na etih zhe svoistvah osnovano i izmerenie vremeni v dannom meste (atomnye chasy). Poetomu nablyudatel', nahodyashiisya v tochke s drugim gravitacionnym potencialom, budet interpretirovat' sdvig chastot kak izmenenie hoda vremeni:

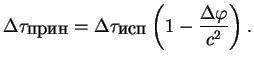$\displaystyle \Delta\tau_{\mbox{prin}}=\Delta\tau_{\mbox{isp}}\left(1-{\Delta\varphi\over{c^2}}\right).$

(8.2)

Ris. 54.

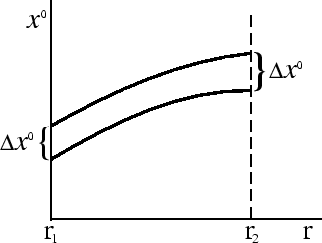
Ran'she my govorili ob izmenenii v gravitacionnom pole metriki voobshe, a teper' vidim bolee konkretno, chto izmenyaetsya techenie vremeni v raznyh tochkah. Eto mozhno interpretirovat' kak izmenenie koefficienta $g_{00}$ pri vremennoi koordinate v metrike. Rassmotrev kak izmenyaetsya $g_{00}$ v slabom pole (t. e. n'yutonovskom sluchae), my uvidim, chto $g_{00}$ igraet rol' n'yutonovskogo potenciala dlya medlennyh chastic.

Rassmotrim staticheskoe gravitacionnoe pole. Po opredeleniyu eto znachit, chto metriku mozhno napisat' v vide

$\displaystyle ds^2=g_{00}(dx^0)^2+g_{\alpha\beta}\,dx^{\alpha}dx^{\beta}\qquad (\alpha,\beta=1,2,3),$

prichem ni $g_{00}$ , ni $g_{0\alpha}$ ne zavisyat ot vremennoi koordinaty

. Pust' v nekotoroi tochke

ispuskayutsya dva svetovyh signala s zapazdyvaniem $\Delta x^0$ i prinimayutsya v tochke

(sm. ris. 54). Poskol'ku $g_{ik}$ ot

ne zavisit, mirovaya liniya vtorogo signala otlichaetsya ot pervoi tol'ko sdvigom po koordinate

na $\Delta x^0$ , t. e. zapazdyvanie signalov v tochke priema po koordinatnomu vremeni tozhe budet $\Delta x^0$ . Odnako nablyudatel' pol'zuetsya ne koordinatnym, a sobstvennym vremenem $\tau$ . Eto sootvetstvuet tomu, chto on v svoei okrestnosti pol'zuetsya metrikoi

$\displaystyle ds^2=c^2d\tau^2-dl^2.$

Interval mezhdu dvumya sobytiyami -- prihodom signalov v tochku

-- invarianten (ne zavisit ot vybora metriki), t. e.

$\displaystyle \sqrt{g_{00}(2)\,}\,\Delta x^0=c\;\Delta\tau_2.$

Otsyuda i iz (8.2) poluchaem svyaz' $g_{00}$ i n'yutonovskogo potenciala $\varphi$ :

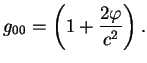
$\displaystyle g_{00}=\left(1+{2\varphi\over{c^2}}\right).$

<< 8.3 Fizika iskrivlennogo ... | Oglavlenie | 9. Sil'nye gravitacionnye polya ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce