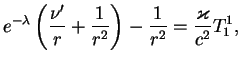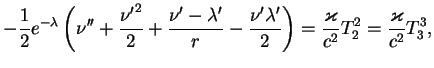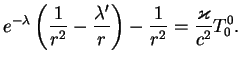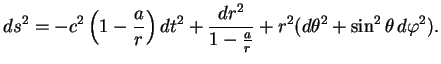Astronet > 9. Sil'nye gravitacionnye polya i stroenie relyativistskih zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 8.4 Gravitacionnoe krasnoe smeshenie. | Oglavlenie | 9.2 Dvizhenie chastic v ... >>

9. Sil'nye gravitacionnye polya i stroenie relyativistskih zvezd

Razdely

9.1 Reshenie Shvarcshil'da

Rassmotrim sfericheski-simmetrichnoe i staticheskoe reshenie uravnenii Einshteina. Vvedem sfericheskie koordinaty, zapisav vyrazhenie dlya intervala v vide

$\displaystyle ds^2=g_{00}\,dt^2+g_{11}dr^2+g_{22}(d\theta^2+\sin^2\theta\,d\varphi^2).$

Vid uglovoi chasti metriki $(d\theta^2+\sin^2\theta\,d\varphi^2)$ sleduet iz trebovaniya sfericheskoi simmetrii. Iz trebovaniya statichnosti nahodim, chto $g_{00}\,g_{11}$ i $g_{22}$ dolzhny byt' funkciyami tol'ko

. Krome togo, dolzhno byt' $g_{01}=0$ , inache ne budet obratimosti vo vremeni. Otsutstvuyut takzhe chleny tipa $g_{r\varphi}$ iz-za sfericheskoi simmetrii.

Opredelim radial'nuyu koordinatu tak, chtoby $g_{22}=r^2$ . Pri takom opredelenii radiusa ploshad' sfery ravna $4\pi r^2$ , a dlina okruzhnosti s centrom v nachale koordinat ravna $2\pi r$ . Odnako eto ne znachit, chto tochka, imeyushaya koordinatu , udalena ot centra na rasstoyanie , tak kak geometriya teper' neevklidova.

Vvedem funkcii $\nu(r)$ i $\lambda(r)$ tak, chto

$\displaystyle g_{00}=-e^{\nu(r)},\,g_{11}=e^{\lambda(r)},$

t. e. metrika priobretaet vid

$\displaystyle ds^2=-e^{\nu(r)}dt^2+e^{\lambda(r)}dr^2+r^2(d\theta^2+\sin^2\theta\,d\varphi^2).$

Iz uravnenii Einshteina

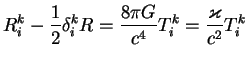
$\displaystyle R^k_i-{1\over 2}\delta^k_i R={8\pi G\over {c^4}}T^k_i={\varkappa\over{c^2}}T^k_i$

posle dovol'no dolgih vychislenii poluchim

$\displaystyle e^{-\lambda}\left({\nu'\over r}+{1\over{r^2}}\right)-{1\over{r^2}}={\varkappa\over{c^2}}T^1_1,$

(9.1)

$\displaystyle -{1\over 2}e^{-\lambda}\left(\nu''+{{\nu'}^2\over 2}+{\nu'-\lambd... ...'\lambda'\over 2}\right)={\varkappa\over{c^2}}T^2_2={\varkappa\over{c^2}}T^3_3,$

(9.2)

$\displaystyle e^{-\lambda}\left({1\over{r^2}}-{\lambda'\over r}\right)-{1\over{r^2}}={\varkappa\over{c^2}}T^0_0.$

(9.3)

Vse ostal'nye uravneniya obrashayutsya v tozhdestva 0=0. Ne diagonal'nye komponenty tenzora energii-impul'sa (tipa $T^{\varphi}_r$ i t. p.) obrashayutsya v nul' vsledstvie sfericheskoi simmetrii (eto oznachaet, chto net skalyvayushih napryazhenii). Otsutstvuet takzhe komponenta

, tak kak etot chlen sootvetstvuet potoku energii po radiusu, a my rassmatrivaem staticheskie resheniya.

My ispol'zovali smeshannye komponenty tenzora . V vyrazhenie $T_{11}$ i $T^{11}$ vhodyat metricheskie koefficienty. Pust' u nas est' metrika

$\displaystyle dl^2=a^2dx^2+b^2dy^2+c^2dz^2,$

(9.4)

kotoraya ekvivalentna metrike

$\displaystyle dl^2={dx'}^2+{dy'}^2+{dz'}^2,$

(9.5)

gde $a\,dx=x'$ , $b\,dy=dy'$ , $c\,dz=dz'$ . Okazyvaetsya, chto vyrazheniya dlya $T_{11}$ , naprimer, raznye v (9.4) i (9.5). V smeshannye komponenty vida

koefficienty $a,\,b,\,c$ ne vhodyat, poetomu oni odinakovy v ishodnoi sisteme i lokal'no-lorencevoi (esli ishodnaya sistema uzhe diagonal'na).

Nachnem s togo, chto budem iskat' reshenie uravnenii (9.1), (9.2), (9.3) v pustote vokrug zvezdy (t. e. polozhim ). Vvedem $f=e^{-\lambda}$ . Togda

$\displaystyle -\lambda'\,e^{-\lambda}=f'$

$\displaystyle \lambda'=-f'/f.$

Teper' dlya uravneniya (9.3) imeem

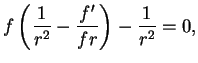
$\displaystyle f\left(\frac{1}{r^2}-{f'\over{fr}}\right)-{1\over{r^2}}=0,$

$f=1-a/r,\,a$ -- const, t. e. $g_{11}=e^{\lambda}=f^{-1}=1/(1-a/r)$ . Vychitaya iz uravneniya (9.1) uravnenie (9.3), poluchim

$\displaystyle \nu'+\lambda'=0\,\Rightarrow\,\nu+\lambda=$ const $\displaystyle .$

Vybor const prosto opredelyaet masshtab vremeni. Poetomu zadadimsya usloviem, chto vdali ot tela, gde $\lambda=0$ , takzhe i $\nu=0$ , t. e. peremennaya

est' vremya izmeneniya dalekim pokoyashimsya nablyudatelem. Togda poluchim

$\displaystyle \nu+\lambda=0$

Otsyuda

$\displaystyle e^{\nu}=g_{00}=1-a/r.$

My poluchili izvestnoe reshenie Shvarcshil'da dlya pustogo prostranstva vokrug sfericheskogo simmetrichnogo tela:

$\displaystyle ds^2=-c^2\left(1-{a\over r}\right)dt^2+{dr^2\over{1-{a\over r}}}+r^2(d\theta^2+\sin^2\theta\,d\varphi^2).$

(9.6)

Pri $r\longrightarrow\infty$ eta metrika perehodit v metriku Minkovskogo.

Iz vyrazheniya (6) vidno, chto pri koefficient pri obrashaetsya v nul', a pri -- v beskonechnost'.

Nablyudatel' na nekotorom radiuse pol'zuetsya lokal'no-lorencevoi sistemoi otscheta:

$\displaystyle ds^2=-c^2d\tau^2+dl^2.$

Dlya pokoyashegosya nablyudatelya v obeih sistemah $dr,\,d\varphi,d\theta=0$ i . Poskol'ku -- invariant, poluchim

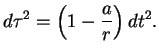
$\displaystyle d\tau^2=\left(1-\frac{a}{r}\right)dt^2.$

Vdali, pri $r\longrightarrow\infty$

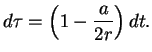
$\displaystyle d\tau=\left(1-{a\over{2r}}\right)dt.$

Tak kak my uzhe vyyasnili svyaz' potenciala s zamedleniem vremeni (razdel 8.4), my vidim, chto

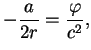
$\displaystyle -{a\over{2r}}={\varphi\over{c^2}},$

gde $\varphi$ -- n'yutonovskii potencial (my ubedimsya v etom eshe raz nizhe, rassmatrivaya dvizhenie chastic), no

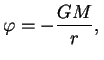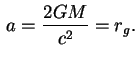
$\displaystyle \varphi=-{GM\over r},\,$ t. e. $\displaystyle \,a={2GM\over{c^2}}=r_g.$

Velichinu

nazyvayut gravitacionnym radiusom (ili radiusom Shvarcshil'da). Dlya zvezdy solnechnoi massy $M=M_\odot=2\cdot10^{33}$ g; $r_g=3\cdot10^5$ sm=3 km (polezno zapomnit'!). Dlya Solnca metriku Shvarcshil'da mozhno primenyat' do poverhnosti $r_s=7\cdot10^{10}$ sm, t. e.

vsyudu malo. Dlya neitronnyh zvezd

dostigaet $0,1\div 0,2$ . Dlya chernoi (nevrashayusheisya!) dyry metrika Shvarcshil'da primenima ko vsei nablyudaemoi oblasti prostranstva, t. e. vplot' do

. Pochemu oblast'

ne nablyudaema (izdali) budet ob'yasneno pozdnee.

<< 8.4 Gravitacionnoe krasnoe smeshenie. | Oglavlenie | 9.2 Dvizhenie chastic v ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce