Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Fizicheskie osnovy stroeniya i evolyucii zvezd
<< 9.2 Dvizhenie chastic v ... | Oglavlenie | 9.4 Obshie svoistva ravnovesiya ... >>

9.3 Sfericheski-simmetrichnoe pole vnutri zvezdy

Zaimemsya teper' uravneniyami v veshestve. Nachnem s uravneniya (3) iz razdela 9.1. Ono soderzhit tol'ko $ \lambda$. Pust' zadano $ T^0_0(r)$.

Izvestnyi metod resheniya neodnorodnyh uravnenii -- metod variacii konstant. My znaem, chto $ f=1-a/r$ udovletvoryaet odnorodnomu uravneniyu. Budem teper' schitat', chto $ a$ ne yavlyaetsya konstantoi. Togda posle podstanovki $ f$ v neodnorodnoe uravnenie vse chleny, ne soderzhashie $ da/dr$, sokratyatsya, a my poluchim

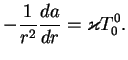
$\displaystyle -{1\over{r^2}}{da\over{dr}}=\varkappa T^0_0. $

Po opredeleniyu

$\displaystyle T^0_0=-\rho c^2=-\varepsilon. $

Togda

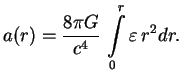
$\displaystyle a(r)={8\pi G\over{c^4}}\,\int\limits^r_0{\varepsilon}\,r^2dr. $

Vvedem velichinu $ m(r)$, takuyu, chto

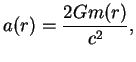
$\displaystyle a(r)={2Gm(r)\over{c^2}}, $

t. e.

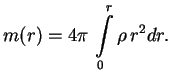
$\displaystyle m(r)=4\pi\,\int\limits^r_0\rho\,r^2dr. $

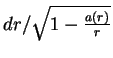Rezul'tat poluchilsya vrode by trivial'nyi. No na samom dele eto ne tak. Element ob'ema vovse ne raven $ 4\pi r^2dr$. Poskol'ku metrika neevklidova, rasstoyanie mezhdu ravno ne $ dr$, a $ e^{\lambda/2}dr$, t. e. $ dr/\sqrt{1-{a(r)\over r}}$, tak chto

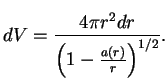
$\displaystyle dV={4\pi r^2dr\over{\left(1-{a(r)\over r}\right)^{1/2}}}. $

Takim obrazom,

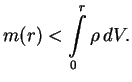
$\displaystyle m(r)<\int\limits^r_0\rho \,dV. $

Polnaya massa est' znachenie $ m$ na krayu zvezdy

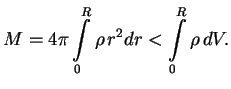
$\displaystyle M=4\pi\int\limits^R_0\rho \,r^2dr<\int\limits^R_0\rho \,dV. $

Polnaya massa men'she summy mass otdel'nyh chastei zvezdy, tak kak ona skladyvaetsya iz mass, kotorye vzaimodeistvuyut gravitacionno.

Esli otdel'nye kuski veshestva (tak zhe szhatye, kak v zvezde) raznesti daleko drug ot druga, to ih polnaya massa byla by ravna

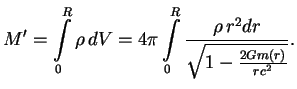
$\displaystyle M'=\int\limits^R_0\rho \,dV=4\pi\int\limits^R_0{\rho\,r^2dr \over{\sqrt{1-{2Gm(r)\over{rc^2}}}}}. $

Vychislim polnoe chislo barionov v zvezde

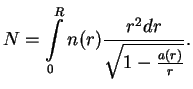
$\displaystyle N=\int\limits^R_0n(r){r^2dr\over{\sqrt{1-{a(r)\over r}}}}. $

Zdes' $ n$ -- plotnost' chisla barionov. Teper' opredelim massu $ M_0$, ravnuyu

$\displaystyle M_0=m_0 N, $

gde $ m_0$ -- massa yadra zheleza $ ^{56}\rm {Fe}$, delennaya na 56, t. e. eto massa bariona, svyazannogo v naibolee ustoichivom yadre.

$ (M_0-M')c^2$ -- eto minimal'naya energiya, neobhodimaya dlya togo, chtoby ``raspylit''' zvezdu na beskonechnost'.

Plotnost' veshestva

$\displaystyle \rho>n\cdot m_0, $

tak kak pri szhatii prihoditsya zatratit' energiyu. Srazu nel'zya skazat', chto bol'she

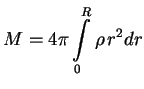
$\displaystyle M=4\pi\int\limits^R_0\rho \,r^2dr $

ili

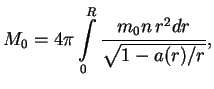
$\displaystyle M_0=4\pi \int\limits^R_0{m_0n\,r^2dr\over{\sqrt{1-a(r)/r}}}, $

tak kak $ \rho>m_0n$, no $ 1/(1-a/r)^{1/2}>1$.

Poetomu v principe energiya svyazi zvezdy

$\displaystyle {\cal E}=(M-M_0)c^2 $

mozhet byt' polozhitel'noi dazhe9.2 v lokal'no-ravnovesnoi sisteme i v raznyh modelyah mozhet imet' raznyi znak. S etim svyazan i vopros o tom, skol'ko vydelyaetsya energii pri obrazovanii zvezdy. My poluchili, chto massa takoi zvezdy

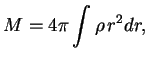
$\displaystyle M=4\pi\int\rho \,r^2dr, $

i polnaya massa barionov togo zhe veshestva na beskonechnosti

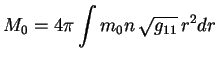
$\displaystyle M_0=4\pi\int m_0n\,\sqrt{g_{11}} \,r^2dr $

gde $ m_0$ -- massa bariona v yadre zheleza. Kak uzhe govorilos', v principe mogut byt' resheniya s $ M>M_0$, hotya ih trudno poluchit' v prirode, tak kak dlya ih obrazovaniya neobhodimo zatratit' energiyu. Eti resheniya neustoichivy otnositel'no razleta na beskonechnost'. Ustoichivy li oni otnositel'no malyh vozmushenii -- skazat' nel'zya bez podrobnyh raschetov. Po-vidimomu vetv' neitronnyh zvezd maloi massy $ M<0,2 M_\odot$ imeet $ {\cal E}>0$, no ustoichiva otnositel'no malyh vozmushenii (sm. nizhe). Resheniya s otricatel'noi energiei svyazi ($ M<M_0$) mogut poluchitsya v rezul'tate estestvennoi evolyucii. My uvidim pozzhe, odnako, chto vse resheniya neustoichivy otnositel'no obrazovaniya chernoi dyry, no po otnosheniyu k bol'shim vozmusheniyam.

Zapishem vyrazhenie dlya massy zvezdy v vide

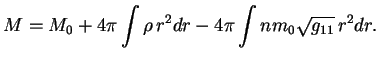
$\displaystyle M=M_0+4\pi\int\rho \,r^2dr-4\pi\int nm_0\sqrt{g_{11}}\,r^2dr. $

Oboznachim cherez

$\displaystyle 4\pi n\sqrt{g_{11}}\,r^2dr=dN $

chislo barionov v sloe ($ r,\,r+dr$).

Vvedem

$\displaystyle m=\rho/n=m_0+E/c^2, $

gde $ E$ -- dobavochnaya energiya, zatrachennaya pri szhatii. S etimi oboznacheniyami

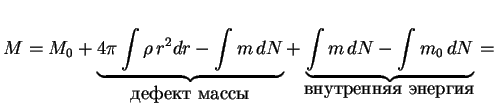
$\displaystyle M=M_0+\underbrace{4\pi\int\rho \,r^2dr-\int m\,dN}_{\mbox{defekt massy}}+ \underbrace{\int m\,dN-\int m_0\,dN}_{\mbox{vnutrennyaya energiya}}= $

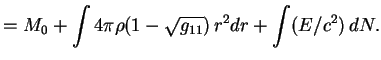
$\displaystyle =M_0+\int 4\pi \rho(1-\sqrt{g_{11}})\,r^2dr+\int(E/c^2)\,dN. $

S tochnost'yu do velichin pervogo poryadka

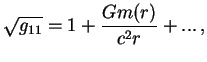
$\displaystyle \sqrt{g_{11}}=1+{Gm(r)\over{c^2r}}+...\,, $

t. e.

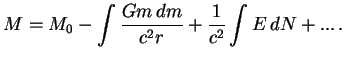
$\displaystyle M=M_0-\int {Gm\,dm\over{c^2r}}+{1\over{c^2}}\int E\,dN+...\,. $

Poluchennoe sootnoshenie bylo tochnym vyrazheniem dlya polnoi energii zvezdy v n'yutonovskoi teorii. Po poryadku velichiny

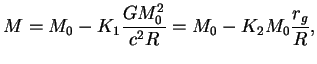
$\displaystyle M=M_0-K_1{GM_0^2\over{c^2R}}=M_0-K_2M_0{r_g\over R}, $

t.e. mozhno skazat', chto tochnye dlya n'yutonovskoi teorii sootnosheniya yavlyayutsya lish' pervymi chlenami razlozheniya po stepenyam $ r_g/R$ dlya energii zvezdy v OTO (po teoreme viriala teplovaya energiya imeet tot zhe poryadok velichiny, chto i gravitacionnaya).

V sleduyushem poryadke poyavlyaetsya chlen $ \sim (r_g/R)^2$. My uzhe znaem, chto pri $ \gamma\longrightarrow 4/3\,\vert{\cal E}_{\mbox{grav}}\vert ={\cal E}_{\mbox{tepl}}$, t.e. chlen $ r_g/R$ ischezaet, i dlya rascheta ustoichivosti stanovyatsya vazhny popravki $ \sim (r_g/R)^2$. Effekty OTO privodyat k tomu, chto pri central'noi plotnosti zvezdy bol'she nekotoroi, massy belyh karlikov nachinayut ubyvat' (sm. ris. 45). Vazhen takzhe uchet OTO dlya sluchaya sverhmassivnyh goryachih zvezd, gde iz-za roli davleniya izlucheniya pokazatel' adiabaty takzhe stremitsya k 4/3.

Ne reshaya poka uravneniya Einshteina do konca, poprobuem uzhe seichas vyyasnit' nekotorye svoistva metriki vnutri zvezdy. Iz-za sfericheskoi simmetrii dostatochno rassmotret' geometriyu odnoi ``ploskosti'', prohodyashei cherez centr, chtoby oharakterizovat' vse trehmerie. Metrika takoi poverhnosti takaya zhe, kak v ploskom trehmernom prostranstve na izognutoi poverhnosti vrasheniya (``tarelke'', sm. ris. 55a). Dlya takoi poverhnosti

$\displaystyle dl^2=r^2d\varphi^2+g_{11}dr^2, $

gde

$\displaystyle g_{11}=\cos^{-2}\alpha. $

Vyyasnim asimptotiku pri $ r\longrightarrow 0$, t. e. v centre. Pust' central'naya plotnost' $ \rho_c$ konechna. Togda $ m(r)\sim r^3$ i, ispol'zuya

$\displaystyle g_{11}=\left[1-{2Gm(r)\over{rc^2}}\right]^{-1}, $

poluchim

$\displaystyle g_{11}=1+$const$\displaystyle \cdot r^2. $

S drugoi storony,

$\displaystyle g_{11}=1+\alpha^2 $

t. e.

$\displaystyle \alpha\sim r. $

Poetomu v centre imeem obyknovennuyu tochku (kasatel'naya gorizontal'na). V principe mozhet byt' osoboe reshenie

$\displaystyle \rho\sim b/r^2\,,\quad m\sim r\,,\quad g_{11}\longrightarrow$const$\displaystyle \ne1\,, $

Ris. 55a.Ris. 55b.

t.e. v centre poyavlyaetsya konicheskaya tochka s beskonechnoi kriviznoi (ris. 55b) -- eto reshenie yavlyaetsya asimptoticheskoi serii nesingulyarnyh reshenii pri $ \rho_i\longrightarrow\infty$.

Rassmotrim teper' asimptotiku pri $ r\longrightarrow\infty$,

$\displaystyle m=M=$const$\displaystyle . $

Imeem

$\displaystyle g_{11}=1+$const$\displaystyle /r=1+\alpha^2, $

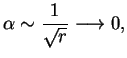
$\displaystyle \alpha\sim{1\over{\sqrt{r}}}\longrightarrow 0, $

t.e. na beskonechnosti prostranstvo opyat' ploskoe (hotya vysota ``tarelki'' i beskonechna).

Prodolzhim reshenie uravnenii. Do sih por my ispol'zovali tol'ko odno uravnenie OTO, kuda vhodit sleva $ g_{11}$ (i ne vhodit $ g_{00}$), a v pravuyu chast' $ T^0_0\sim \rho$.

Ochen' vazhno zametit', chto do sih por ne podrazumevalos', chto raspredelenie plotnosti ravnovesno. Neobhodim tol'ko pokoi ( $ \dot \lambda,\,\dot \nu=0$). Skorosti ravny nulyu, a uskoreniya mogut byt' lyubymi. Uslovie ravnovesiya my nigde ne ispol'zovali. Poetomu poluchennoe vyrazhenie dlya $ M$ udobno v dal'neishem ispol'zovat' dlya issledovaniya ustoichivosti zvezdy.

Vernemsya k ravnovesnym zvezdam. Sleduyushie uravneniya (vmeste s usloviyami stacionarnosti $ \dot \lambda,\,\dot \nu=0$), kuda vhodit davlenie, dadut uslovie ravnovesiya. Ogranichimsya sluchaem paskalevoi zhidkosti

$\displaystyle T^1_1=T^2_2=T^3_3=P. $

V uravnenie (1) iz razdela 9.1 vhodit tol'ko $ d\nu/dr$, a v (9.2) eshe $ d^2\nu/dr^2$. Differenciruya pervoe uravnenie, isklyuchaya $ d^2\nu/dr^2,\,d\nu/dr,\,d\lambda/dr,\,\nu$ i $ \lambda$, posle algebraicheskih preobrazovanii poluchaem uravnenie gidrostaticheskogo ravnovesiya

$\displaystyle {dP\over{dr}}=-{G\left(\rho+{P\over{c^2}}\right)\left(m+4\pi P{r^3\over{c^2}}\right) \over{r^2\left(1-{{2Gm\over{c^2r}}}\right)}}. $

Napomnim, chto v n'yutonovskoi teorii

$\displaystyle {dP\over{dr}}=-{G\rho m\over{r^2}}. $

Otlichiya OTO ot n'yutonovskoi teorii takovy: 1) vmesto $ \rho $ vhodit $ \rho+P/c^2$, t. e. davlenie ``vesit''; 2) sila prityazheniya zavisit ne tol'ko ot $ m$, no i ot $ P$:

$\displaystyle m\longrightarrow m+4\pi Pr^3/c^2 $

(yasno, chto eti popravki sushestvenny, kogda $ P/c^2$ sravnimo s $ \rho $, t.e. dlya relyativistskogo veshestva);    3) pri $ r\longrightarrow r_g(r)$ imeem $ dP/dr\longrightarrow \infty$, uskorenie $ g\longrightarrow\infty$, tak kak v znamenatele v uravnenii ravnovesiya v OTO stoit $ r(r-r_g)$ vmesto n'yutonovskogo $ r^2$.

Nado imet' vvidu, chto fizicheskii gradient davleniya raven

$\displaystyle {dP\over{dl}}={dP\over{\sqrt{g_{11}}dr}}\sim{1\over{\sqrt{1-r_g/r}}}, $

poetomu uskorenie rastet ne kak $ (1-r_g/r)^{-1}$, a po zakonu $ (1-r_g/r)^{1/2}$. Na nashei dvumernoi poverhnosti, ``izobrazhayushei'' metriku, pri $ r=r_g$ stenki ``tarelki'' stanovyatsya vertikal'nymi (ris. 56).

Ris. 56.

Zadavshis' uravneniem sostoyaniya $ P(\rho)$, mozhno integrirovat' uravnenie ravnovesiya i uravnenie nepreryvnosti

$\displaystyle dm=4\pi\rho r^2dr $

pri proizvol'no vybrannom znachenii v centre $ \rho_c$ i sootvetstvuyushim $ P_c$. Pri lyubom razumnom uravnenii sostoyaniya my poluchim padayushee reshenie, idushee v nul' na krayu zvezdy.

Chto budet, esli central'naya plotnost' ochen' velika ( $ \rho_c\longrightarrow\infty$), ne poluchitsya li beskonechnaya massa? Voz'mem stepennoe uravnenie sostoyaniya. Pust' $ n$ -- plotnost' barionov, $ v=1/n,\,E$ -- energiya na barion. V izentropicheskom sluchae $ dE=-Pdv$. Poskol'ku $ E=\rho c^2/n$,

$\displaystyle c^2d\left({\rho\over n}\right)=-P\,d\left({1\over n}\right)={P\over{n^2}}\,dn. $

Otsyuda

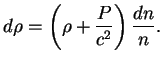
$\displaystyle d\rho=\left(\rho+{P\over{c^2}}\right){dn\over n}. $

Esli $ \rho=An^k$, to

$\displaystyle P=c^2(k-1)\rho=(k-1)\varepsilon. $

Zdes' my vypisali obshee stepennoe uravnenie ($ k=4/3$ -- ul'trarelyativistskii gaz, $ k=2$ -- predel'no zhestkoe uravnenie sostoyaniya, tak kak v etom sluchae skorost' zvuka $ (\partial P/\partial \rho)^{1/2}=c$).

Pust' $ \rho=b/r^2$,

$\displaystyle P=c^2(k-1)\,b/r^2. $

Togda

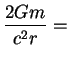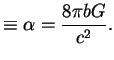
$\displaystyle {2Gm\over{c^2r}}=$const$\displaystyle \equiv \alpha={8\pi bG\over{c^2}}. $

Ris. 57.

Podstavlyaya $ \rho,\,P$ i $ m$ v uravnenie ravnovesiya, poluchim

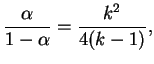
$\displaystyle {\alpha\over{1-\alpha}}={k^2\over{4(k-1)}}, $

t.e. sushestvuet reshenie, gde ``tarelka'' idet na konus, no dlya kazhdogo pokazatelya $ k$ konus imeet svoi naklon.

Tekushaya massa $ m\sim r$, no eto spravedlivo tol'ko v oblasti bol'shih plotnostei, zatem $ \rho $ spadaet bystree, chem $ 1/r^2$, i $ m$ stanovitsya konechnym. Takim obrazom, dazhe pri $ \rho_c\longrightarrow\infty$ massa ostaetsya konechnoi! Pri etom obshaya massa zvezdy zavisit ot togo znacheniya plotnosti $ \rho_1$, pri kotorom uravnenie sostoyaniya perestaet byt' stepennym, t. e. gde narushaetsya proporcional'nost' $ P$ i $ \rho $.

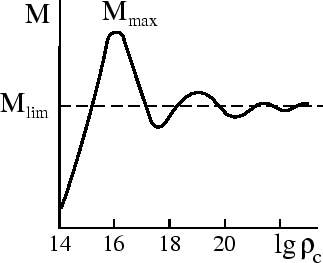
Analiticheskoe issledovanie dlya stepennyh uravnenii sostoyaniya i chislennye raschety pokazyvayut, chto zavisimost' $ M(\rho_c)$ vedet sebya kak na ris. 57, t. e. posle pervogo maksimuma voznikayut kolebaniya krivoi $ M(\rho_c)$. Analiz pokazyvaet, chto vse resheniya za pervym maksimumom neustoichivy. Znachenie maksimal'noi massy $ M_{\max}$ poluchaetsya raznym pri raznyh uravneniyah sostoyaniya. Dlya gaza svobodnyh neitronov Oppengeimer i Volkov poluchili $ M_{\max}=0,7M_\odot$9.3. Sovremennye raschety, uchityvayushie mezhnuklonnye vzaimodeistviya, dayut dlya neitronnyh zvezd $ M_{\max}= 1,8\div 2,4\,M_\odot$. Eshe raz napomnim, chto massa zdes' ponimaetsya kak istochnik gravitacionnogo polya dlya vneshnego nablyudatelya. Massa togo zhe chisla barionov sushestvenno bol'she $ M_{0\;\max}\sim(2,2\div3,2)\,M_\odot$, tak chto energiya svyazi otricatel'naya. Neitronnye zvezdy bol'shoi massy ustoichivy otnositel'no razleta na beskonechnost', pri ih obrazovanii vydelyaetsya energiya $ \sim 20\%$ nachal'noi energii pokoya, t.e. velichina, vo mnogo raz prevyshayushaya yadernuyu energiyu.

Zadacha. Izvestno, chto pri predel'no zhestkom uravnenii sostoyaniya $ P=\rho c^2=$const$ \cdot n^2$ (Ya.B.Zel'dovich) v n'yutonovskoi teorii massa zvezdy $ M\longrightarrow\infty$ pri $ P_c\longrightarrow\infty$. S pomosh'yu uravneniya gidrostatiki pokazat', chto v OTO dazhe v sluchae neszhimaemoi zhidkosti ( $ P\longrightarrow\infty,\,n=n_0=$const) massa ostaetsya konechnoi pri $ P_c\longrightarrow\infty$.


<< 9.2 Dvizhenie chastic v ... | Oglavlenie | 9.4 Obshie svoistva ravnovesiya ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 3.0 [golosov: 120]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya